Unterrichtseinsichten - Schuljahr 2008/2009 - Physik 10c

Kinematik

Anmerkung: Erscheinen die Zeichen > und < mit dazwischen liegenden (scheinbaren) Leerplätzen, so ist dort ein Text verborgen, der durch Markierung sichtbar wird. Beispiel: >Test<

2008-08-22

Will man Bewegungen untersuchen, so muss man sich darüber klar sein, von welchem Bezugssystem man die untersuchten Vorgänge beschreiben will.
Um zu üben, wie man Vorgänge von verschiedenen Standpunkten aus sehen kann, haben wir einige Beispiele untersucht:

Wie sieht man (theoretisch) von der Sonne aus die Bahn des Erd-Mondes?
>Der Mond bewegt sich auf einer verschlungenen Schleifenkurve.<
Dreht sich der Mond um sich selbst? Und wenn ja, wie lange gebraucht er dazu?
>Ja, einmal im Monat. Deshalb sieht man von der Erde aus auch immer dieselbe Seite des Mondes<
Wie sieht man vom Mond aus die Erde? Ändert sich mit der Zeit der Ort der Erde am Himmel? Ändert sich mit der Zeit das Aussehen der Erde?
>Die Erde steht am Himmel immer an derselben Stelle. Da sich die Erde dreht, kann man jeden Ort auf der Erde einmal in 24 Stunden sehen.<

Wir haben erkannt, dass es gar nicht so einfach ist, sich in einen anderen Beobachtungsstandort hineinzudenken.

2008-08-26

Die Überlegungen der letzten Stunde haben wir abgeschlossen mit Beispielen zu verschiedenen Bezugssystemen (Zug - Bahnsteig, Fahrradfahrer - ruhender Beobachter).
Die Spur, die eine Glühlampe am Fahrradreifen zieht, kann man sich mit diesem Programm simulieren lassen.

2008-08-29

Bewegungen kann man geeignet untersuchen, indem man misst oder bestimmt, welche Werte die zurückgelegte Strecke und die Geschwindigkeit im Lauf der Zeit annehmen.
Dazu trägt man die entsprechenden Werte z.B. in einer Tabelle oder einem Diagramm auf.
Bei konstanter Geschwindigkeit zeigt das t-x-Diagramm eine schräge Gerade. Je steiler die Gerade ist, desto höher ist die Geschwindigkeit.
Ein Videoanalyse-Programm nimmt uns dabei viel Arbeit ab.
Wir haben in dieser Stunde das Programm Viana kennen gelernt. Es ist unter der Adresse http://didaktik.physik.uni-essen.de/viana/ herunterzuladen.
Hier die in Eurer Klasse aufgenommene avi-Videos mit der waagrechten und senkrechter Bewegung.
Die Umrechnung zwischen den Einheiten km/h und m/s für die Geschwindigkeit geschieht nach folgender Formel:
1 m/s = 3,6 km/h (1 km = 1000 m und 1 h = 60 min = 3600 s)

2008-09-02

Thema der Stunde war die Darstellung von geradlinig-gleichförmigen Bewegungen (konstante Geschwindigkeit) in Diagrammen und die Beschreibung durch Geradengleichungen.
Wer noch einmal grundlegende Dinge über Geradengleichungen nachlesen möchte und einige Übungen zu Geradengleichungen nicht unwichtig findet, kann hier und sonst unter Google fündig werden.
Bei Ursprungsgeraden im t-s-Diagramm beginnt der zurückgelegte Weg mit der Strecke 0.
Liegt keine Ursprungsgerade vor, startet der Weg nicht bei 0, sondern bei anderen Werten.
Beispiel: Wenn man auf die Autobahn fährt, steht auf dem Kilometerstein in den seltensten Fällen 0 km.
Der Beginn der Zählung liegt meist an einem anderen Ort als an der Autobahnauffahrt.
Entsprechend der Geradengleichung y=m·x+b schreibt man bei Bewegungen mit konstanter Geschwindigkeit s=v·t+s₀.
Dabei ist s der Weg zur Zeit t. v ist die Geschwindigkeit der Bewegung und s₀ ist der Weg, an dem die Bewegung zur Zeit t=0 beginnt.
Mit der Bewegungsgleichung s=v·t+s₀ kann man eine der beteiligten physikalischen Größen berechnen, wenn die anderen Größen gegeben sind.

2008-09-05

Bei physikalischen (und anderen) Messungen macht man zwangsläufig Fehler. Man unterscheidet zwischen

statistischen Fehlern (Ablesefehler, Fehler auf Grund zufälliger Ereignisse, Abweichungen vom Erwartungswert) und
systematischen Fehlern (Grund liegt im Messgerät, falscher Bedienungsweise, Einfluss äußerer Störungen (Wärme, Luftdruck, usw.)).

Statistische Fehler treten mit jedem Messgerät und bei jedem Messenden auf, lassen sich aber minimieren.
Systematische Fehler dagegen sind durch den Versuchsaufbau bedingt und lassen sich nicht beliebig klein machen (es sei denn, der Versuchsaufbau würde abgeändert).
Werden zwei Messgrößen addiert oder subtrahiert, so ergibt sich der Gesamtfehler aus der Addition der absoluten Messfehler.
Werden zwei Messgrößen multipliziert oder dividiert, so ergibt sich der Gesamtfehler aus der Addition der relativen Fehler.
Hat eine Strecke die Länge 5m und misst man sie auf +-5cm genau, so ist "5cm" der absolute Fehler und 5cm/5m = 5cm/500cm = 5/500 = 1/100 = 1% der prozentuale Fehler.
Der absolute Fehler ist also die maximale tatsächliche Abweichung vom richtigen Wert,
der relative Fehler ist das Verhältnis von der Abweichung zum tatsächlichen Wert.

2008-09-09

Fährt ein Fahrradfahrer an der Ampel los, so beschleunigt er zunächst, d.h. er wird immer schneller. Wenn er seine normale Fahrgeschwindigkeit erreicht hat, wird er sich mit konstanter Geschwindigkeit weiter bewegen.
Ein ähnlicher Vorgang wird durch einen Versuch auf der Luftkissenfahrbahn nachgestellt:
Der Messstreifen kommt dadurch zustande, dass jeweils nach 1/10 s ein Punkt an der Stelle des Wagens gesetzt wird:
Die Auswertung zeigt folgende Tabelle:

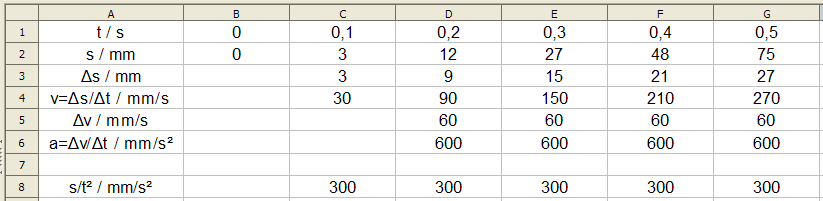
Die 2. Zeile gibt an, an welchem Ort sich der Wagen zu der Zeit, die in der 1. Zeile steht, befindet.
Bilden wir die Differenzen der Streckenstücke, ergeben sich die Strecken, die jeweils in 1/10 s zurückgelegt werden. Diese Werte sind ein Maß für die Geschwindigkeit des Wagens. Man sieht, dass zu Beginn der Wagen schneller wurde und zum Schluss mit konstanter Geschwindigkeit fährt.
Die Differenzen der Differenzen (unterste Zeile) sind in jedem der Abschnitte konstant.
Hausaufgabe: Sucht eine Funktionsklasse, bei der die Differenzen der Differenzen der Funktionswerte für x=1, 2, 3, 4, 5, ... konstant sind.
Die Graphen (links: t-s-Diagramm, rechts: t-Δs-Diagramm) zeigen, dass links die unterschiedlichen Bewegungsarten nicht so gut zu erkennen sind, rechts dagegen sehr gut.

2008-09-10

Die beiden Diagramme der letzten Stunde zeigen, dass die Bewegung bis zur Zeit 0,5s einheitlich ist:
Δs und damit die Geschwindigkeit v=Δs/Δt (Δt ist konstant 1/10s) nimmt mit der Zeit t konstant zu. Es gilt also v~t.
Mit dem Proportionalitätsfaktor a ergibt sich v = a · t (Geradengleichung) . Die Konstante a nennt man Beschleunigung.
Um a zu berechnen, ermittelt man die Steigung mit Hilfe eines Steigungsdreiecks: a=Δv/Δt. Die Werte kann man der folgenden Tabelle entnehmen:

Bis zum Zeitpunkt 0,5s ergibt sich also der konstante Wert a = 600mm/s².
Schwieriger ist das links stehende t-s-Diagramm auszuwerten.
Der erste Teil der Kurve sieht nach Exponentialfunktion oder Parabel aus.
Um herauszufinden, welche Kurvenart vorliegt, hilft folgende Überlegung:
Oben haben wir gesehen, dass die 2. Differenzenfolge eine Konstante ergibt (bis zum Zeitpunkt 0,4s).
Nun untersuchen wir in folgender Tabelle, ob das eine Eigenart der Exponentialfunktion oder der Funktion einer Parabel ist. Dazu werden die Funktionen y=2^x und y=x² herangezogen.

Die Differenzenfolgen wiederholen sich und zeigen keine gleichen Werte. Die Kurve wird also wohl keine Exponentialfunktion sein.

Hier sind ab der 2. Differenzenfolge die Werte konstant. Die gesuchte Funktion könnte also eine Parabel sein. Es gilt also s~t² oder mit dem Proportionalitätsfaktor c: s=c·t².
Die Bewegung wird also durch die Gleichungen s = c · t² und v = a · t beschrieben. Besteht ein Zusammenhang zwischen den Werten a und c?
c=s/t² wurde in der Tabelle oben berechnet und ergibt den Wert 300 mm/s² , also halb so viel wie a.
Würde man weitere Versuche zur Beschleunigung durchführen, würde man erkennen, dass immer gilt c = 1/2 · a.
Damit erhalten wir für die beschleunigte Bewegung, bei der die Geschwindigkeit konstant zunimmt, die Bewegungsgleichungen .

2008-09-19

Die Überlegungen in den letzten Stunden zur Geschwindigkeit bei der beschleunigten Bewegung waren noch sehr qualitativer Art.
Eine genauere Herleitung ist auf diesem Arbeitsblatt und dem dazu gehörigen GeoGebra-Arbeitsblatt zu finden.
Zu den Bewegungen mit a=const. und v=const. haben wir eine Aufgabe gerechnet, in der die Bewegungsgleichungen benutzt werden mussten:

geradlinig gleichförmige Bewegung: s=v·t ; v=const. ; a=0
gleichförmig beschleunigte Bewegung: s=1/2·a·t² ; v=a·t ; a=const.

Der Rechengang ist auf in diesem Übungsblatt dokumentiert.

2008-09-23

Bislang haben wir nur Bewegungen betrachtet, die bei s=0 (Koordinatenursprung) und mit v=0 (aus der Ruhe heraus) erfolgen.
Startet man bei einem beliebigen s-Wert und mit einer Geschwindigkeit ungleich 0, so müssen die Gleichungen folgendermaßen erweitert werden.
Dabei bedeutet s₀ den Startpunkt und v₀ die Startgeschwindigkeit.
Geradlinig gleichförmige Bewegung (Geschwindigkeit ist konstant)

s(t) = v · t + s₀
v(t) = v₀ = const.
a(t) = 0

Gleichförmig beschleunigte Bewegung (Beschleunigung ist konstant)

s(t) = 1/2 · a · t² + v₀ · t + s₀
v(t) = a · t + v₀
a(t) = a₀ = const.

2008-09-24

Weitere Übung zu den Bewegungsgleichungen:
Ein PKW (Länge 3m) fährt mit 100km/h auf der Landstraße. Als seine vordere Stoßstange 50m von der hinteren Stoßstange eines mit der Geschwindigkeit 80km/h fahrenden 12m langen Lastwagens entfernt ist, setzt der PKW-Fahrer zum Überholen an und fährt dabei mit gleichbleibender Geschwindigkeit am Lastwagen vorbei. Er schert so ein, dass seine hintere Stoßstange dabei 50m vor der vorderen Stoßstange des Lastwagens ist.
Fragen: Wie lange dauert der Überholvorgang? Welche Strecke legt der PKW beim Überholen zurück?
Bitte als Hausaufgabe weiter rechnen.

2008-09-30

Besprechung der Hausaufgabe.
Eine Beispielrechnung (mit anderen Werten) seht ihr hier.

2008-10-01

Es zeigte sich, dass die Beispielaufgabe noch nicht richtig verstanden war.
Ein nochmaliges Durchrechnen der Lösung (neu!) ergab einen Einblick in erhebliche Defizite beim Bearbeiten von Gleichungen und Gleichungssystemen.
Bitte unbedingt mathematische Grundfertigkeiten wiederholen und gründlich üben!

2008-10-07

Freier Fall

Vorstellungen zum Fallen in der Antike und heute.
Bitte neben der Eingangsseite auch die weiterführenden Seiten beachten (u.a. Film zum Fall in Luft und Vakuum).
Versuch zum freien Fall (Versuchsaufbau und Animation).
Bitte den Versuch auswerten: Tabelle mit Strecken und Zeiten, dann Graphik und rechnerische Auswertung.

2008-10-08

Besprechung der Versuchsauswertung. Ergebnis: Die Beschleunigung hat etwa den Wert 10 m/s².
Gerechnet wird wegen der beschleunigten Bewegung mit der Formel s = 1/2 · a · t² bzw. a = 2 s / t².

2008-10-28

Die Ähnlichkeit des in der letzten Stunde berechneten Wertes zum Ortsfaktor g=10 N/kg ist verblüffend, vor allem, wenn man durch Rechnung feststellt, dass m/s² = N/kg.
Wir haben gesehen, dass man nicht entscheiden kann, ob man sich in Ruhe auf der Erdoberfläche mit dem Ortsfaktor g=10 N/kg befindet oder ob man fern aller großen Massen im Weltraum mit der Beschleunigung a=10 m/s² beschleunigt wird.
Näheres dazu könnt Ihr hier nachlesen.
Auch die anderen Teile der Internetseite http://www.einstein-online.info/de/ sind sehr lesenswert!
Zu hoffen ist, dass die Bewegung der Schülerinnen und Schüler nicht nur beim Probealarm (wie heute) mit konstanter Geschwindigkeit erfolgt und nicht mit konstanter Beschleunigung, sondern auch im Ernstfall.

2008-10-29

Auf Grund widriger Umstände konnte folgendes Problem nur kurz diskutiert werden:
Ein schwerer Gegenstand (Goldkugel der Prinzessin) fällt in einen 10 m tiefen Brunnen. Berechnet die Fallzeit.

2008-11-05

Lösung der Aufgabe vom 2008-10-29:
Da eine beschleunigte Bewegung vorliegt, kann die Formel s=1/2·g·t² benutzt werden.
Aufgelöst nach t ergibt sich . Mit s=10m und g=10 m/s² ergibt sich etwa t=1,4.
Schaut Euch doch mal an, was ich mit der Parallelklasse besprochen habe: Berechnung der Brunnentiefe.

2008-11-11

An mehreren Beispielen haben wir besprochen, dass sich verschiedene Bewegungen eines Körpers ungestört überlagern.
Lässt man z. B. in einem fahrenden Zug einen Gegenstand fallen, so fällt er für den Beobachter im Zug senkrecht nach unten.
Zu dieser Bewegung kommt aber für einen Beobachter auf dem Bahnsteig noch die Bewegung des Zuges hinzu.
Die geradlinig gleichförmige Bewegung des Zuges überlagert sich mit der beschleunigten Fallbewegung so, dass vom Bahnsteig aus gesehen der Gegenstand eine gekrümmte Fallkurve besitzt.
Diese Erkenntnis kann man bei folgender Aufgabe anwenden:
Ein Turmspringer springt vom 5m-Brett mit der Geschwindigkeit v₀=1m/s senkrecht nach oben (in positive y-Richtung) und fällt dann herunter (in negativer y-Richtung) bis aufs Wasser.
Frage: Wie lange dauert der Fall des Turmspringers?

Ohne die Erdanziehungskraft würde der Turmspringer mit konstanter Geschwindigkeit nach oben fliegen.
Da diese Geschwindigkeit konstant ist, gilt die Bewegungsgleichung s=v·t.
Der erste Teil der Bewegung führt also zur zurückgelegten Strecke y₁=v₀·t.
Ohne das Hochspringen würde der Turmspringer nur die Fallbewegung durchführen.
Diese Bewegung ist beschleunigt mit der konstanten Fallbeschleunigung g. Es gelten die Bewegungsgleichungen s=1/2·g·t² und v=g·t.
Der zweite Teil der Bewegung führt also zur zurückgelegten Strecke y₂=-1/2·g·t² (negativ, weil der Körper nach unten fällt).
Insgesamt legt der Körper also eine Strecke y zurück, die sich berechnet aus y = y₁ + y₂ = v₀·t - 1/2·g·t².
Bedingung ist, dass der Springer unten bei -5 auf der y-Achse ankommt. Also gilt:
-5 = v₀·t - 1/2·g·t².
Setzt man die Werte ein (ohne Einheiten), so ergibt sich
-5 = t - 5·t² oder 5·t² - t - 5 = 0 oder t² - 1/5·t - 1 = 0
Mit der p-q-Formel findet man dann die Lösungen t₁=-0,9 und t₂=1,1 . Der Sprung dauert also etwa 1,1 Sekunden.
Die negative Lösung t₁ zeigt an, dass die Bewegung nicht unbedingt auf dem 5m-Brett begonnen haben muss, sondern dass der Springer schon vorher in Bewegung gewesen sein kann und zum Zeitpunkt 0 das 5m-Brett passiert hat. 0,9s vor dem Absprung vom 5m-Brett müsste er dann auf Wasserhöhe gewesen sein.

Hausaufgabe: Welche maximale Höhe über dem Wasser erreicht der Springer? (Tipp: Wir haben schon gefunden, dass die Geschwindigkeit am obersten Punkt 0 sein muss)

2008-11-12

Wenn Ihr Schwierigkeiten habt, Euch den in der letzten Stunde besprochenen Ablauf des Sprungs vorzustellen, hilft Euch vielleicht folgendes GeoGebra-Arbeitsblatt:
Wir haben festgestellt, dass die maximale Sprunghöhe mit 5cm nicht realistisch ist.
Berechnet zur nächsten Stunde, wie hoch die Absprunggeschwindigkeit sein muss, damit eine Sprunghöhe von 40cm erreicht wird.

2008-11-18

Lösung der Hausaufgabe:

gegeben sind s_max=0,4m und g=10m/s².
gesucht ist v₀.
benutzt werden die bekannten Bewegungsgleichungen

s=v·t für v=const.
s=1/2·g·t² und v=g·t für a=const.=g

Die speziellen Bewegungsgleichungen für den senkrechten Wurf ergeben sich daraus, dass sich 2 Bewegungen ungestört überlagern, die geradlinig gleichförmige Bewegung nach oben und der freie Fall (beschleunigte Bewegung) nach unten.

s(t)=v₀·t-1/2·g·t²
v(t)=v₀-g·t

Bei Erreichen des höchsten Punktes der Flugbahn gilt s(t)=s_max und v(t)=0.

s_max=v₀·t-1/2·g·t²
0=v₀-g·t

Aus der 2. Gleichung ermittelt man v₀ und setzt den Wert in die erste Gleichung ein:

v₀=g·t
smax=g·t·t-1/2·g·t²=g·t²-1/2·g·t²=1/2·g·t²

Daraus ergibt sich t zu
Einsetzen in die Gleichung v₀=g·t gibt
Die Absprunggeschwindigkeit muss also etwa 2,8m/s betragen.

Bitte unbedingt diese Aufgabe zu Hause selbstständig rechnen!
Noch besser ist es, die Aufgabe Mama, Papa, Oma, Opa und dem Hund so zu erklären, dass alle bis auf einen sie verstanden haben. Dann habt Ihr sie auch verstanden.

2008-11-19

Weiterführende Aufgaben, bei denen die maximale Höhe angenommen wird, lassen sich mit der Formel leicht lösen.
Beispiele: "Für eine gegebene Anfangsgeschwindigkeit ist die maximale Höhe zu berechnen." oder "Auf einem Himmelskörper misst man die Anfangsgeschwindigkeit und die maximale Höhe. Auf welchem Himmelskörper befindet man sich? (g berechnen)"
Wird ein Körper nicht senkrecht nach oben geworfen, sondern waagrecht, also rechtwinklig zur freien Fallbewegung, so muss man den Weg und die Geschwindigkeit in x- und in y-Richtung beschreiben:

s_x=v₀·t Weg in x-Richtung - Bewegung mit konstanter Geschwindigkeit
v_x=v₀
s_y=-1/2·g·t² Weg in y-Richtung - Bewegung mit konstanter Beschleunigung
v_y=-g·t

Die Bahnkurve des fallenden Körpers ergibt sich aus den Termen für s_x und s_y:

aus s_x=v₀·t folgt t=s_x/v₀
eingesetzt in s_y=-1/2·g·t² ergibt s_y=-1/2·g·(s_x/vt)²=-g/(2·v₀²)·s_x²
da also s_y~s_x², liegt eine Parabelbahn vor

2008-11-25

An einer Straße der Breite 20m stehen zwei Häuser, ein rotes Haus der Höhe 10m und ein grünes Haus der Höhe 8m:

Vom roten Haus wird eine Kugel waagrecht nach rechts mit der Geschwindigkeit 10m/s geworfen, vom grünen Haus eine Kugel mit 20m/s waagrecht nach links.
Die Bahnen der Kugeln kreuzen sich zwischen den Häusern.
Frage 1: Wie lange dauert der Fall der beiden Kugeln?
Lösung (g=10m/s²):

Bewegungsgleichungen links: x_links=v_links·t und y_links=-1/2·g·t²+10
Bewegungsgleichungen rechts: x_rechts=-v_rechts·t+20 und y_rechts=-1/2·g·t²+8
Kugel-links: Setze y_links=0. Daraus folgt 0=-1/2·g·t²+10 oder t²=2 bzw. t=1,41. der Fall dauert also etwa 1,41s.
Kugel-rechts: Setze y_rechts=0. Daraus folgt 0=-1/2·g·t²+8 oder t²=8/5 bzw. t=1,26. der Fall dauert also etwa 1,26s.

Frage 2: Wo treffen die Kugeln auf dem Boden auf?
Lösung:

linke Kugel: t=1,41s in die Gleichung für x_links einsetzen: x_links=v_links·t=10m/s·1,41s=14,1m.
rechte Kugel: t=1,26s in die Gleichung für x_rechts einsetzen: x_rechts=-v_rechts·t=-20m/s·1,26s+20m=-5,2m. (Die rechte Kugel würde also an der Hauswand auftreffen)

Frage 3: Können sich die Kugeln am Kreuzungspunkt der Fallkurven treffen?
Lösung (g=10m/s²):

Wir stellen eine Tabelle auf und vergleichen die Höhen der Kugeln zu verschiedenen Zeiten (Annahme: Die Falltiefe ist nicht begrenzt):

Zeit 0 ; y_links=10 ; y_rechts=8
Zeit 1 ; y_links=5 ; y_rechts=3
Zeit 2 ; y_links=-10 ; y_rechts=-12
Zeit 3 ; y_links=-35 ; y_rechts=-37

Es fällt auf, dass ylinks immer um 2 größer ist als y_rechts.
Dass das so sein muss, erkennt man an den Bewegungsgleichungen:
Der Summand -1/2·g·t² kommt sowohl bei y_links als auch bei y_rechts vor. Nur die Zahlenwerte 10 und 8 sind unterschiedlich. Dieser Unterschied bleibt natürlich bei verschiedenen Zeiten erhalten, weil die Zahlen konstant sind und sich der Summand -1/2·g·t² in beiden Gleichungen gleich ändert.
Folgerung: Da immer ein Unterschied von 2m in der Höhe besteht, können die Kugeln sich nicht treffen.

2008-11-26

Weitere Übung zum waagrechten und senkrechten Wurf als Vorbereitung auf die Arbeit.
Denkt bitte bei der Bearbeitung der Aufgaben an folgende Schritte:

Bewegungsgleichungen für die beiden behandelten Bewegungsarten parat haben:

geradlinig-gleichförmige Bewegung (v=const.)

s=v₀·t
v=v₀

gleichförmig beschleunigte Bewegung (a=const.)

s=1/2·a·t²
v=a·t

was ist gegeben?
was ist gesucht?
Modellierung: Welche Bewegungsarten kommen vor in x-Richtung und in y-Richtung?
Aufstellen der aktuellen Bewegungsgleichungen für die x-Richtung und für die y-Richtung.
Nebenbedingungen aus der Aufgabe in die Bewegungsgleichungen einsetzen.
die gesuchten Größen berechnen.

Behandelte Bewegungsarten

freier Fall

y=-1/2·g·t²

senkrechter Wurf

y=v₀·t-1/2·g·t²

waagrechter Wurf

x=v₀·t
y=-1/2·g·t²

Liegt der Ursprung des Koordinatensystems nicht im Anfangsort der Bewegung, müssen noch Korrekturen an den Gleichungen vorgenommen werden.

2008-12-02

Wiederholung zur Arbeit

2008-12-03

Klassenarbeit 1

2008-12-09

Schallplatten gab es früher (und zum Teil auch noch heute) als Langspielplatte (12'' Durchmesser, Laufzeit ca. 20 Minuten) mit 33 1/3 rpm und als Single (7'' Durchmesser, Laufzeit ca. 5 Minuten) mit 45 rpm.
Die kleinere Platte muss sich aus Qualitätsgründen schneller drehen, da sonst die in der Rille gespeicherten Informationen nicht genügend Platz hätten.
rpm steht für "Rotationen pro Minute" und bedeutet, dass sich die große Platte 33 1/3-mal pro Minute dreht und die Single 45 mal pro Minute.
Der Winkel, der in einer bestimmten Zeit zurückgelegt wird, ist für alle Teile der Schallplatte gleich.
Sitzen Personen in einem Karussell, so ist es nicht sinnvoll, die Bewegung des Karussells durch die Bahngeschwindigkeit einer einzelnen Person zu beschreiben, da die Geschwindigkeit davon abhängig ist, in welchem Abstand zur Drehachse sich die Person befindet.
Besser ist es, eine Größe zu finden, die für alle Personen auf dem Karussell gleich ist. Dazu bietet sich der Winkel Δφ an, der in einer bestimmten Zeit Δt zurückgelegt wird.
Man definiert so als Winkelgeschwindigkeit ω=Δφ/Δt. Diese Winkelgeschwindigkeit gilt für alle Personen auf dem Karussell.
Nimmt man als Winkeldifferenz bei der Winkelgeschwindigkeit den Vollwinkel 2π, so gehört dazu die Umlaufdauer T und es gilt ω=2π/T.
Für die Bahngeschwindigkeit gilt bei einer vollen Umdrehung mit dem Radius r: v=2π·r/T=(2π/T)·r=ω·r
Linktipp zum Thema "Kreisbewegung"

2009-01-07

Besprechung und Rückgabe der Klassenarbeit 1 [ Klassenarbeit | Lösung ]

2009-01-09

Versuche zum Umgang mit der Zentripetalkraft und der Zentripetalbeschleunigung:

Am Drehtisch wird außen eine Halterung angebaut.
Ein Ball soll nun so an die Halterung gelegt werden, dass diese ihn beim Drehen so hält, dass er nicht vom Tisch herunter fällt.

1. Versuch:
Drehrichtung gegen den Uhrzeigersinn. Der Ball wird nicht gehalten, sondern fliegt von der Drehscheibe.
2. Versuch:
Merkwürdigerweise wird so der Ball beim Drehen durch die beiden Auflagepunkte gehalten, sodass er nicht herunter fällt.
Warum ist das so?
Offensichtlich wird der Ball in Richtung der Halterung gedrückt, sodass diese ihn durch eine Kraft, die zum Zentrum der Drehscheibe gerichtet ist, halten kann.
Diese Kraft heißt Zentripetalkraft oder Zentralkraft.
Der Ball "spürt" eine Kraft, die ihn radial nach außen treibt, die Zentrifugalkraft. In Wirklichkeit wirkt diese Kraft gar nicht. Die Zentrifugalkraft ist eine Scheinkraft.
Sie kommt dadurch zu Stande, dass der Ball eigentlich tangential die Scheibe verlassen "möchte" und damit die Scheibe nach außen verlassen möchte. Daran wird er aber gehindert und so "spürt" er die Kraft, die ihn gegen das Hindernis drückt.

Herleitung der Formel für die Zentripetalbeschleunigung: a_z=v²/r. (Siehe Buch Seite 23)

2009-02-04

Besprechung von Aufgaben zur Kreisbewegung im Buch auf Seite 29
Das vereinbarte Passwort war übrigens zu kurz. Wenn Ihr stattdessen den Plural des Passworts benutzt, wird es gehen (mit ä=ae, ü=ue, ö=oe, ß=ss).

2009-02-10

Kurzinformationen zu den Themen Foucault und Coriolis. Näheres dazu aus dem Unterricht anderer Klassen:
Versuch: Rollt eine Kugel auf eine Drehscheibe, so führt ihr Weg auf der Scheibe (Reibung nicht berücksichtigt) auf einer Geraden entlang.
Ein Beobachter auf der drehenden Scheibe sieht dagegen die Kugel auf einer gekrümmten Bahn rollen. Für ihn wirkt auf die Kugel ständig eine seitliche Kraft, die die Kugel aus ihrer geraden Richtung ablenkt. Wegen der gekrümmten Bahn muss die Bewegung eine beschleunigte Bewegung sein.
Die zugehörige Beschleunigung a_C nennt man Coriolisbeschleunigung und die scheinbar wirkende Kraft Corioliskraft.
Da die Kraft und die Beschleunigung nicht wirklich existieren (für einen außerhalb der Scheibe ruhenden Beobachter), sondern nur vom auf der Drehscheibe mitbewegten Beobachter so gesehen wird, nennt man die Corioliskraft auch Scheinkraft.
Wir haben auf der drehenden Scheibe gerade Kreidestriche ("gerade" für einen außerhalb der Scheibe ruhenden Beobachter) gezeichnet und dann beim Stillstand der Scheibe (auf der Scheibe ruhender Beobachter) gesehen, dass die Kugel gekrümmte Spuren (etwa kreis- bzw. spiralförmig) hinterlassen hat.
Eine Kugel (rot) rollt mit konstanter Geschwindigkeit auf einer still stehenden Drehscheibe vom Mittelpunkt auf einem Radius (schwarze Strecke) zum Außenrand (Bild links oben, zum Vergrößern auf das Bild klicken)
Dreht sich nun die Scheibe im Gegenuhrzeigersinn unter der rollenden Kugel und schließt man Reibungskräfte aus, so wird die rote Kugel weiterhin ihre Richtung (in der Abbildung senkrecht nach unten) behalten. Der auf der Scheibe eingezeichnete Radius wird sich aber mit der Scheibe drehen.
Von außen betrachtet bewegt sich die Kugel also geradlinig gleichförmig.
Ein mitbewegter Betrachter auf der Drehscheibe dagegen wird die Kugel auf einer gekrümmten Bahn sehen (siehe Bild rechts unten).
Die Kugel beschreibt für ihn eine aus zwei Teilbewegungen überlagerte Bewegung:

Vom Mittelpunkt aus bewegt sich die Kugel mit konstanter Geschwindigkeit geradlinig zum Rand der Scheibe.
Vom eingezeichneten Radius aus bewegt sich die Kugel mit konstanter Geschwindigkeit auf einem Kreisbogen fort (siehe Kreisbögen der gelben Kreissektoren).

Die zusammengesetzte Bewegungsgleichung ergibt sich aus folgenden Überlegungen:
Geschwindigkeit der Kugel ist v_K.
Radius der Scheibe ist r_S.
Winkelgeschwindigkeit der Scheibe ist ω.
Der zurückgelegte Kreisbogen wird mit b bezeichnet.
Für die radiale Bewegung gilt wegen s=v·t : r_S=v_K·t
Für die Kreisbewegung gilt wegen s=v·t und v=ω·r : b=ω·r_S·t=ω·(v_K·t)·t=ω·v_K·t² .
Der mitbewegte Beobachter sieht also die Kugel in einer beschleunigten Bewegung der Form b=1/2·a·t² .
Durch Vergleich der beiden Beziehungen b=ω·v_K·t² und b=1/2·a·t² ergibt sich die Gleichung ω·v_K=1/2·a bzw. a=2·ω·v_K .
Diese Beschleunigung nennt man Coriolis-Beschleunigung und bezeichnet man mit a_C .
a_C=2·ω·v_K beschreibt also eine Beschleunigung, durch die ein mitbewegter Beobachter die Kugel schneller werden sieht.
Da eine Richtungsänderung eines Körpers nur durch eine Kraft bewirkt werden kann, sieht der mitbewegte Beobachter beim Ablenken der Kugel eine Kraft, die in Wirklichkeit gar nicht vorhanden ist, also eine Scheinkraft. Diese Kraft nennt man Corioliskraft. Sie bewirkt u. a. die Entstehung der gekrümmten Bahnen, auf denen sich die Winde auf der Erde bewegen.
Anmerkung: Den Zusammenhang zwischen Kräften und Beschleunigungen werden wir demnächst behandeln.
Die Windrichtungen um Hoch- und Tiefdruckgebiete lassen sich mit der Corioliskraft erklären.
Hier einige Links zu Hoch- und Tiefdruckgebieten, Wikipedia-Artikel zu Tiefdruck, Atmosphärenphysik, Seminararbeit zur planetarischen Ludftzirkulation

weiter mit Dynamik