Unterrichtseinsichten - Schuljahr 2008/2009 - Physik 10c

Dynamik

• Nach Aristoteles benötigt ein Körper einen bestimmten Impetus, um sich bewegen zu können. Ist dieser Impetus aufgebraucht, kommt der Körper zur Ruhe. 
• Newton dagegen ging im Trägheitsgesetz davon aus, dass ein Körper solange im Zustand der Ruhe oder der geradlinig gleichförmigen Bewegung bleibt, solange keine äußeren Kräfte auf ihn einwirken.
  Aus Erfahrung weiß man zwar, dass jeder Körper irgendwann zur Ruhe kommt.
  Der Widerspruch erklärt sich daraus, dass wir nahezu immer mit Reibung (an Luft, Gegenständen, usw.) bei Versuchen zu rechnen haben. 
• Wir haben mehrere Versuche zur Trägheit gesehen, die auf dieser Seite gezeigt werden.

• Bei der Wiederholung zum Trägheitssatz haben wir gesehen: Die Trägheit einer Masse hängt von der Größe der Masse ab. Je größer eine Masse, desto schlechter kann sie in Bewegung gesetzt oder abgebremst werden.
• Zur genaueren Untersuchung der Zusammenhänge dienen folgende Versuche mit der Luftkissenfahrbahn:
• Zwei Fahrbahnwagen gleicher Masse werden durch eine Feder auseinandergedrückt.
  Auf beide Wagen wirkt deshalb die gleiche Kraft.
  
  In gleicher Zeit bewegen sich jeder Wagen um die gleiche Strecke nach außen.
• Wird die Masse des einen Wagens auf das Doppelte vergrößert, bewegt sich der Wagen mit der doppelten Masse nur halb so weit wie der Wagen mit der kleineren Masse.
  
  Da der schwerere Wagen nur halb so weit kommt wie der leichtere Wagen, ist die Geschwindigkeit des schwereren Wagens halb so groß wie die Geschwindigkeit des leichteren Wagens.
• Allgemein gilt: Haben die Wagen die Massen m₁ und m₂ und die Geschwindigkeiten v₁ und v₂, so gilt m₁·m₂=v₁·v₂.
  In unserem Versuch gilt m₁=m, m₂=2·m, v₁=v und v₂=1/2·v. Dann folgt: m₁·v₁=m·v und m₂·v₂=2·m·1/2·v=m·v
• Wenn die antreibende Kraft in zwei Versuchen gleich ist, so ist auch das Produkt m·v gleich. Man setzt p=m·v und nennt p den Impuls.
  Die Impulse des rechten und des linken Fahrbahnwagens sind also gleich.
• Hier der Versuchsaufbau und eine Simulation.

• In der letzten Stunde haben wir gesehen, dass der Gesamtimpuls vor dem Loslassen der Wagen gleich 0 war und dass das auch für die Situation nach dem Losgleiten so war.
• Theoretisch sollte auch für den Fall, dass die Wagen sich zu Beginn bewegen, dann zusammenstoßen und danach vereint oder getrennt weiter fahren, der Gesamtimpuls immer konstant sein.
  Diesen Impulserhaltungssatz drückt man durch folgende Gleichungen aus:
  Gemeinsames Weiterfahren nach dem Stoß:  m₁·v₁+m₂·v₂=(m₁+m₂)·v'
  Getrenntes Weiterfahren nach dem Stoß:   m₁·v₁+m₂·v₂=m₁·v₁'+m₂·v₂'
• Zur Überprüfung dieser Gesetzmäßigkeit haben wir die Bewegung zweier Wagen untersucht, die aufeinander zu gleiten und sich nach dem Stoß gemeinsam weiter bewegen:
  Die Geschwindigkeit der Wagen wird dadurch ermittelt, dass die Zeit gemessen wird, in der ein auf dem Gleiter befestigter Streifen eine Lichtschranke verdunkelt.
  Wagen 1 gleitet nach rechts. Er hat die Masse 94g und sein Streifen hat die Breite 1,1cm. Gemessen wird die Zeit 54,88ms.
  Wagen 2 gleitet nach links. Er hat die Masse 190g und sein Streifen hat die Breite 1,0cm. Gemessen wird die Zeit 27,99ms.
  Gemeinsam gleiten die Wagen 1 und 2 nach links. Sie haben die Masse 284g und beim Streifen mit der Breite 1,0cm werden 57,31ms gemessen.
• Auswertung:
• Wagen1: Geschwindigkeit: v₁=1,1cm/54,88ms=0,020cm/ms
• Wagen2: Geschwindigkeit: v₂=1,0cm/27,99ms=0,036cm/ms
• Impuls vor dem Stoß: m₁·v₁+m₂·v₂=94g·0,020cm/ms-190g·0,036cm/ms=-4,90g·cm/ms
• Wagen1 und Wagen2 nach dem Stoß: v'=1,0cm/57,31ms=0,017cm/ms
• Impuls nach dem Stoß: (m₁+m₂)·v'=284g·(-0,017cm/ms)=-4,96g·cm/ms 
• Die Minuszeichen geben an, dass sich der Wagen nach links bewegt. Die Ergebnisse für den Impuls vor und nach dem Stoß stimmen nahezu überein.

• Besprechung der Hausaufgabe. Das Ergebnis deutet darauf hin, dass bei der Messung zum Ende der letzten Stunde grobe Messfehler vorliegen mussten, weil sich der Impulserhaltungssatz aus dem Ergebnis nicht erschloss. In der nächsten Stunde werden wir den Versuch noch einmal mit genauerer Durchführung wiederholen.
• Der Impulserhaltungssatz besagt, dass vor und nach einer Wechselwirkung zwischen Körpern der Gesamtimpuls konstant bleibt.
• Neu kennengelernte Schreibweise:
  Werden mehrere Impulse addiert, so kann man die ausgeschriebene Summe mit dem Summenzeichen abkürzen:
  

• Besprechung der Hausaufgabe: Der Körper mit der Masse m₁=100g und der Geschwindigkeit v₁=10m/s trifft auf den Körper mit der Masse m₂=300g und der Geschwindigkeit v₂=-20m/s.
  Nach dem Stoß fahren beide Körper vereint mit der Geschwindigkeit v' weiter. Berechne v'.
  Lösung: Es gilt die Formel m₁·v₁+m₂·v₂=(m₁+m₂)·v', die sich nach v' auflösen lässt: (m₁·v₁+m₂·v₂)/(m₁+m₂)=v'.
  Daraus folgt: v'=(100·10-300·20)/(100+300)m/s=(1000-6000)/400m/s=-5000/400m/s=-12,5m/s
• Experimente mit der Luftkissenfahrbahn: Elastische Stoß: 2 Wagen prallen zusammen und werden durch die dabei zusammengedrückte Feder wieder Getrennt zurückgestoßen.
  Zugrunde liegt die Gleichung m₁·v₁+m₂·v₂=m₁·v₁'+m₂·v₂'
  Ergebnisse der 3 Messungen (die Zeiten geben an, wie lange es gedauert hat, bis eine 5cm breite Blende die Lichtschranke passiert hat):
  m₁=96g, m₂=193g
  Wegen der Richtung (rechts nach links) müssen t₂ und t₁' negativ genommen werden.
  
  Einsetzen der Werte in die Gleichung für den Impulserhaltungssatz liefert folgende Ergebnisse:
  8,7 und 7,2 ; 12,6 und 8,8 ; 9,6 und 9,4
  Die Ergebnisse des 1. und 2. Versuchs passen nicht gut bzw. gar nicht. Der dritte Versuch bestätigt den Impulserhaltungssatz.

• Die Rechenarbeit bei der Auswertung eines Versuchs wie in der letzten Stunde kann mit dem Taschenrechner schnell erledigt werden:
  Im Menüpunkt STAT>EDIT werden in Liste L1 die Zeiten für den linken Wagen, in Liste L2 die Zeiten für den rechten Wagen eingegeben.
  Liste L3 erhält dann die Formel L3=5/L1 und Liste L4 die Formel L4=5/L2.
  Damit werden die Geschwindigkeiten für die beiden Wagen berechnet.
  5 ist die Breite des durch die Lichtschranke gezogenen Streifens.
  Mit den Massen 96g für den linken und 193g für den rechten Wagen folgt dann in Liste L5 die Berechnung der Impulse vor bzw. nach dem Stoß: L5=96*L3+193*L4.
     

• In folgenden 2 Versuchen soll untersucht werden, wie sich ein ändernder Impuls auf einen Körper auswirkt:
  
  Eine Kugel wird auf einen Holzklotz geschossen. Trifft sie dabei in einem Auffangbehälter auf und wird dort festgehalten, so wird der Holzklotz etwas zur Seite ausgelenkt.
  Trifft die Kugel auf dem Holz auf und wird zurückgeschleudert, so wird der Holzklotz um einen größeren Winkel ausgelenkt.
  Eure Vermutung, mit Kugel sei der Holzklotz schwerer als ohne Kugel und deshalb würde er im 1. Versuch nicht so weit ausgelenkt, könnte im Prinzip zutreffen. Da die Kugel aber wesentlich leichter ist als der Holzklotz, muss noch ein anderer Grund vorhanden sein. 
      
  
  Die Deutung des Versuchs werden wir in der nächsten Stunde vornehmen.

• Im Bild links hat die Kugel nach dem Abschuss den Impuls p=m·v. Nach dem Auftreffen ist sie im Prinzip in Ruhe (wird aber vom schwingenden Holzklotz mitgenommen). Ihr Impuls ist nun 0.
  Im Bild rechts hat die Kugel nach dem Abschuss auch den Impuls p=m·v. Nach dem Auftreffen würde sie im Idealfall zurückreflektiert werden und hätte dann den Impuls p=-m·v.
  Die Änderung des Impulses würde also 2·m·v betragen, wäre also doppelt so groß, wie im 1. Fall. Deshalb schwingt hier der Holzklotz auch weiter aus.
• Bei größerer Impulsänderung wird der Holzklotz weiter bewegt, es muss also eine größere Kraft auf ihn gewirkt haben.
  Würde die Impulsänderung über einen größeren Zeitraum hin erfolgen, so würde die wirksame Kraft kleiner sein.
  Auf Grund dieser Abhängigkeiten: größerer übertragener Impuls --> größere Kraft ; Übertragung des Impulses über lange Zeit --> kleinere Kraft definiert man Kraft als .
• Für den Fall, dass die Masse konstant bleibt, kann die gefundene Formel noch folgendermaßen umgeformt werden:
  
• Man erhält so die Newtonsche Bewegungsgleichung F=m·a (auch Grundgleichung der Mechanik oder in der Form  2. Newtonsches Gesetz genannt).

• Übungsaufgabe aus dem Buch Seite 53

• Beispiel für das Vorgehen bei einer komplexen Messung an Hand der Messung eine speziellen Kraft (Kraft bei Drehbewegung)
  
  Versuchsaufbau: 
  
  Die Vorbesprechung hat ergeben, dass die Kraft F abhängig sein wird von der Masse m des Wagens, von der Winkelgeschwindigkeit ω der Drehbewegung und von dem Radius r, mit dem der Wagen um das Zentrum kreist.
  Ist eine Größe von mehreren anderen Größen abhängig, so müssen bei einer Messung sinnvollerweise alle Größen konstant gehalten werden bis auf zwei Größen, deren Abhängigkeit man untersuchen will.
  Beim vorliegenden Versuch muss man also 3 Fälle unterscheiden:
• F und r variabel, m und ω konstant
• F und m variabel, r und ω konstant
• F und ω variabel, r und m konstant.
• In einer ersten Probemessung bestimmten wir die Umlaufdauer des Drehkörpers.
  Wir haben gesehen, dass man ein genaueres Ergebnis erhält, wenn man nicht nur die Zeit für 1 Umlauf misst, sondern für z. B. 10 Umläufe und dann das Ergebnis durch die Anzahl der Umläufe dividiert.

• Durchführung der ersten beiden Messungen
• F und r variabel, m und ω konstant: m=54g, T=1,999s
  Messergebnis:
• F und m variabel, r und ω konstant: r=0,18m, T=1,999s
  Messergebnis:

• Zur Auswertung der Messreihen und vor allem zur Benutzung des Taschenrechners siehe die Ausführungen auf der Seite für die 10e (2009-03-26 und 2009-04-16).
• Wiederholung zur Klassenarbeit (siehe dazu auch die älteren Physik-Klassenarbeiten).

• Wiederholung zur Klassenarbeit

• Klassenarbeit 2

• Gegenstände, die im Erdschwerefeld unter sich freien Raum haben oder die sich bewegen haben die Eigenschaft gegenüber auf dem Boden liegenden oder in Ruhe befindlichen Gegenständen, von selbst etwas bewirken zu können. Der im freien Raum befindliche Gegenstand kann beim Herunterfallen etwas zerstören, genau wie derjenige, der mit großer Geschwindigkeit gegen ein Hindernis stößt.
  Diese Eigenschaft, Arbeit verrichten zu können, nennt man Energie.
• Unmittelbar einsichtig ist, dass ein Körper um so mehr Energie hat, je höher er über dem Boden ist. Ebenso klar ist, dass ein schnellerer Körper mehr Energie hat als ein langsamer Körper.
  Wie genau hängt aber die Energiemenge von der Höhe h und von der Geschwindigkeit v eines Körpers ab?
  Um das Herauszufinden, wandelt man am besten die eine in die andere Energieform um. 
• So wird die Lageenergie eines Körpers, der sich in der Höhe h befindet, beim Herunterfallen in Bewegungsenergie umgewandelt, so dass er beim Auftreffen auf den Boden eine Geschwindigkeit erreicht hat, deren Bewegungsenergie der vorher vorhandenen Lageenergie entspricht.
• Umgekehrt wird ein nach oben geworfener Gegenstand, der zu Beginn entsprechend seiner Geschwindigkeit Bewegungsenergie besitzt, am höchsten Punkt seiner Bahn diese gesamte Bewegungsenergie in Lageenergie umgewandelt haben.
• Zur Untersuchung der Energieumwandlung von Lageenergie E_L in Bewegungsenergie E_B wird auf einer Luftkissenfahrbahn ein Wagen durch eine angehängte Masse beschleunigt. Die erreichte Geschwindigkeit wird mit Hilfe einer Lichtschranke (kleiner roter Punkt) bestimmt.
  
  In Abhängigkeit von der Fallhöhe des schwarzen Massekörpers wird die Verdunkelungs-Zeit gemessen und dann mit der Formel v~1/t ein Maß für die Geschwindigkeit gefunden.
   
  In L1 stehen die Fallhöhen des Massestücks, in L2 die gemessenen Zeiten. 
  In L3 wird dann mit 1000/L2 ein Maß für die Geschwindigkeit gefunden. Da es nicht auf absolute Werte, sondern nur auf Proportionalitäten ankommt, wurde zur besseren Lesbarkeit der Ergebnisse der Faktor 1000 gewählt.
  Bei der Suche nach der mathematischen Funktion, die die Messwerte am besten beschreibt, muss man darauf achten, dass der Punkt (0/0) vom Graph möglichst gut getroffen wird, weil für die Fallhöhe 0 cm die Geschwindigkeit 0 m/s gilt.
  Eine Geradengleichung kann deshalb nicht die Lösung sein. 

• Wir haben gesehen: Wegen des Punktes (0/0) kann eine Gerade keine Lösung für das Problem der letzten Stunde sein.
       
• Eine quadratische Regression ergab eine relativ gute Übereinstimmung, die Parabel bedeutete aber, dass bei größeren Fallhöhen die Geschwindigkeit wieder geringer würde.
  Das ist aber Unsinn, denn je größer die Fallhöhe, desto größer auch die Geschwindigkeit.
        
     
• Die Lösung des Problems erhielten wir, indem wir L3 waagrecht und L1 senkrecht abgetragen haben. Mit einer quadratischen Regression erhielten wir ein physikalisch sinnvolles Ergebnis und gute Übereinstimmung mit den Messwerten.
  Ergebnis: h~v² . Um die doppelte Geschwindigkeit zu erhalten, muss man also den Körper aus der 4-fachen Höhe fallen lassen.
     
• h und v sind Repräsentanten für die Lageenergie und für die Bewegungsenergie.
  Wir sehen: Die Lageenergie ist proportional zur Höhe des Körpers.
  Die Bewegungsenergie nimmt quadratisch mit der Geschwindigkeit zu. Doppelte Geschwindigkeit bedeutet also 4-fache Energie. Im Straßenverkehr beachten!
• Neuer Versuch: Eine gespannte Feder beschleunigt den Fahrbahnwagen. Welchen Zusammenhang gibt es zwischen dem Spannungsgrad der Feder und der Geschwindigkeit des Wagens?
  Messwerte: s=2cm --> t=265,96ms ; s=4cm --> t=198,34ms ; s=6cm --> t=183,11ms ; s=8cm --> t=105,24ms ; s=10cm --> t=83,94ms

• Besprechung und Rückgabe der Klassenarbeit 2 (Aufgaben, Lösung)
• In der letzten Stunde haben wir gesehen, dass die Höhe h, aus der ein Körper fällt, proportional zum Quadrat der Geschwindigkeit ist, die der Körper maximal erreicht: h~v² .
• Nun soll der Zusammenhang zwischen der Spannenergie einer Feder und der Bewegungsenergie untersucht werden.
  Bei gleicher Masse hängen diese Energien von der Verlängerung Δs der Feder und der Geschwindigkeit v des Körpers ab.
  Ein Wagen der Luftkissenbahn wird durch eine gespannte Feder beschleunigt. Gemessen werden die Verlängerung Δs der Feder und die Zeit t, die der Wagen benötigt, damit eine auf ihm befindliche Papierschablone eine Lichtschranke durchquert.
  
• Messwerte, eingegeben in den GTR: in L1 Verlängerung der Schraubenfeder in cm, in L2 Zeit zum Durchqueren der Lichtschranke in ms.
  In L3 wird die Formel L3=5000/L2 eingegeben. Damit wird die Geschwindigkeit des Wagens in cm/s berechnet.
  Erläuterung: es gilt v=S/t mit S=5cm und t gemessen in ms. Möchte man die Einheit cm/s erhalten, so muss t durch 1000 dividiert werden oder, da t im Nenner steht, der Zähler des Bruches mit 1000 multipliziert werden.
           
  Da die Geschwindigkeit 0 ist, wenn die Feder gar nicht verlängert wurde, wird dieser "Messwert" in den Spalten L1 und L3 hinzugefügt.
  Vorsicht: In L2 darf unten nicht 0 stehen, da die Verdunkelungszeit bei der Geschwindigkeit 0 cm/s unendlich lang wäre.
  Da die Messpunkte in etwa auf einer Geraden liegen, wird eine lineare Regression durchgeführt.
          
    
• Ergebnis: Die Geschwindigkeit des Wagens ist proportional zur Verlängerung der Feder: v~Δs.
  Aus dieser Proportionalität folgt v²~(Δs)² .
  Damit gibt es folgende charakteristische Größen für die einzelnen Energiearten:
  Lageenergie E_L --- h ; Bewegungsenergie E_B --- v² ; Spannenergie einer Feder E_S --- (Δs)² .
• Wie die genauen Gleichungen für die Energien lauten, werden wir in den nächsten Stunden besprechen.

• Die Lageenergie E_L hängt außer von der Höhe auch noch von der Masse ab. Bei doppelter Masse sollte die Energie doppelt so groß sein.
  Auch der Ortsfaktor g sollte in der Energie vorkommen, denn auch eine große Masse kann zur Lageenergie nichts beitragen, wenn sie nicht durch eine Gravitationskraft beschleunigt wird.
  So hat man dann die Lageenergie (oder auch potenzielle Energie E_Pot) definiert als E_L=m·g·h.
• Energie kann man sich als gespeicherte Arbeit denken. Hebt man einen Körper der Gewichtskraft F_G=m·g um die Höhe h an, so hat man die Arbeit W=m·g·h verrichtet. Der Betrag dieser Arbeit ist gleich dem der Lageenergie.
  Trägt man in einem Diagramm die Gewichtskraft gegen die Höhe auf, so ergibt sich für den Flächeninhalt zwischen Funktionsgraph und x-Achse der Wert der Energie:
  
   
• Auch die Bewegungsenergie E_B (oder auch kinetische Energie E_Kin) wird zusätzlich zum gefundenen Faktor v₂ von der Masse m abhängen.
  Gewinnt ein Körper Bewegungsenergie durch eine konstante Kraft, die auf einer Strecke Δs wirkt, so gilt:
  F·Δs=Δp/Δt·Δs=Δp·Δs/Δt=Δp·v. Δp ist dabei der gesamte Impuls, der bei der Geschwindigkeit v erreicht wurde.
  Trägt man auch hier im v-p-Koordinatensystem den entsprechenden Graph auf, so ergibt sich eine Ursprungsgerade und zwischen Ursprungsgerade und v-Achse als Flächeninhalt der entsprechende Energiewert: E_B=1/2·m·v²
  
• Ähnlich verläuft die Herleitung der Spannenergie E_Sp:
  Nach dem Hookeschen Gesetz F~s bzw. F=D·s wächst die Kraft linear mit der Auslenkung der Feder.
  Graph und Flächenberechnung ergeben E_Sp=1/2·D·s².
  
• Mit Hilfe der Integralrechnung lassen sich diese Herleitungen später eleganter lösen.

• Energie kann man nicht aus dem Nichts erzeugen und Energie verschwindet nicht einfach.
  Würde Energie aus dem Nichts erzeugt werden können, so wäre es möglich, ein Perpetuum mobile (1, 2) zu bauen, eine Maschine, die ohne Energiezufuhr ewig laufen würde und darüber hinaus auch noch überschüssige Energie erzeugen könnte.
  Energie verschwindet nicht einfach (z.B. wenn ein Ball nach mehrmaligen Hüpfen auf dem Boden liegen bleibt), sondern wird durch Reibungseffekte in innere Energie bzw. Wärme (=Bewegungsenergie der Atome und Moleküle) umgewandelt.
• Folge ist, dass Energien sich ineinander umwandeln können und dass die Gesamtenergie eines Systems immer konstant ist. Es gilt der Energieerhaltungssatz (1, 2).
• Wir haben folgende Aufgabe gerechnet:
  2 Körper bewegen sich aufeinander zu und stoßen elastisch zusammen. Nach dem Stoß bewegen sie sich mit unterschiedlicher Geschwindigkeit voneinander fort.
  Die Massen der Körper sind m₁=5kg, m₂=10kg und die Geschwindigkeiten vor dem Stoß v₁=2m/s und v₂=-8m/s. Gesucht sind die Geschwindigkeiten v₁' und v₂' nach dem Stoß.
  Lösung: Da 2 Größen unbekannt sind, benötigen wir ein Gleichungssystem mit 2 Gleichungen.
  Wir nehmen dazu den Impulserhaltungssatz und den Energieerhaltungssatz, setzen die Werte ein, lösen die eine Gleichung nach v₂' auf und setzen das Ergebnis in die andere Gleichung ein:
  
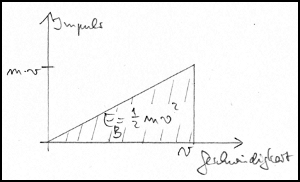
  Impulserhaltungssatz     m₁·v₁+m₂·v₂=m₁·v₁'+m₂·v₂'
  Energieerhaltungssatz   1/2·m₁·v₁²+1/2·m₂·v₂²=1/2·m₁·v₁'²+1/2·m₂·v₂'²   ---> (dividiert durch 1/2)  m₁·v₁²+m₂·v₂²=m₁·v₁'²+m₂·v₂'²
  Rechnungen ohne Einheiten, da sich die Einheit kg herausteilt und das Ergebnis in der Einheit m/s abgezeigt wird.
  Impulserhaltungssatz    5·2+10·(-8)=5·v₁'+10·v₂'    --->   10-80=5·v₁'+10·v₂'   --->   -70=5·v₁'+10·v₂'   --->   v₂'=(-70-5·v₁')/10=-7-1/2·v₁'  
  Energieerhaltungssatz   5·2²+10·(-8)²=5·v₁'²+10·v₂'²   --->   20+640=5·v₁'²+10·v₂'²   --->   660=5·v₁'²+10·v₂'²  --->
  660=5·v₁'²+10·(-7-1/2·v₁')²=5·v₁'²+490+70v₁' +5/2·v₁'²   --->   15/2·v₁'²+70·v₁'-170=0    --->   v₁'²+28/3·v₁'-68/3=0   --->
  1. Lösung:
  v₁'=-14/3+√(196/9+204/9)=-14/3+√(400/9)=-14/3+20/3=6/3=2
  daraus folgt  v₂'=-7-1/2·2=-7-1=-8
  Man sieht, dass v₁=v₁' und v₂=v₂' . Die Körper haben sich also gar nicht getroffen, sondern sind aneinander vorbeigefahren.
  2. Lösung:
  v₁'=-14/3-√(196/9+204/9)=-14/3-√(400/9)=-14/3-20/3=-34/3≈-11,3
  daraus folgt  v₂'=-7-1/2·(-34/3)=-7+34/6=-42/6+34/6=-8/6=-4/3≈-1,3
  Beide Körper bewegen sich also nach dem Stoß nach links, der leichtere Körper mit 11,3m/s und der schwerere Körper mit 1,3m/s.
• Weitere Übungsaufgaben zum zentralen elastischen Stoß.

• Besprechung der Zeugnisnoten und Wiederholung des Rechengangs der letzten Stunde.
  Links zum zentralen elastischen Stoß: Theorie zu Sonderfällen - Allgemeine Herleitung zur Bestimmung der Geschwindigkeiten nach dem Stoß.

• Versuch zur Bestätigung des Energieerhaltungssatzes am Beispiel einer Schraubenfederschwingung.
      
  Der untere Ansatz einer Schraubenfeder befindet sich auf der Höhe 1.
  Nachdem die Masse m angehängt wird ist der untere Ansatz der sich in Ruhe befindenden Schraubenfeder auf der Höhe 2.
  Nun wird die Schraubenfeder noch ein Stück per Hand nach unten ausgelenkt, so dass der untere Ansatz auf der Höhe 3 zu finden ist.
  Auf der Höhe 4 ist eine Lichtschranke angebracht, die die Verdunkelungszeit t durch eine Papierfahne der Länge L misst. Man nimmt näherungsweise an, dass sich während der Verdunkelung die Schraubenfeder mit konstanter Geschwindigkeit bewegt und kann dann diese Geschwindigkeit aus den Messergebnissen berechnen.
  Anschließend wird die Gesamtenergie aus der potenziellen Energie E_Pot, der Spannenergie E_Sp und der kinetischen Energie E_Kin an der Höhe 4 berechnet und mit Gesamtenergien an anderen Orten verglichen. Dann sollte zu sehen sein, dass die Gesamtenergie auf allen Höhen identisch ist.
• Messwerte: m=260g; L=2cm; Höhe1=730mm; Höhe2=503mm; Höhe 3=350mm; Höhe4=530mm; t=0,0455s
  2 weitere Messungen bei verschiedenen Werten von Höhe 3:
  H3=300mm; t=0,0260s
  H3=250mm; t=0,0079s
• Auswertung in der nächsten Stunde.

• Auswertung der Messung aus der letzten Stunde:
• Die Gesamtenergie auf der Höhe 4 soll berechnet werden. Es liegen dort Energien in Form von E_Pot, E_Sp und E_Kin vor.
  Es gilt: E_gesamt=E_Pot+E_Sp+E_Kin =m·g·h+1/2·D·s²+1/2·m·v²
• Die Gewichtskraft F_G der Masse m entspricht der Kraft F, die die Schraubenfeder um die Länge s₀ verlängert (von 1 nach 2, also 227mm=0,227m).
  Man kann also schreiben: F_G=F ---> m·g=D·s₀ --->  D=m·g/s₀ .
• Den 0-Punkt der potenziellen Energie legen wir in die Ebene 3. Damit ist h der Abstand zwischen den Ebenen 3 und 4, also 180mm=0,18m.
• s ist die Verlängerung der Schraubenfeder von Ebene 1 zu Ebene 4, also 200mm=0,2m.
• v berechnet sich aus der Hohe L der Papierfahne und der gemessenen Zeit t: v=L/t.
• m=0,26kg ; L=0,02m ; g=9,81m/s²
• Es gilt also (Einheiten werden weggelassen): E_gesamt4=0,26·9,81·0,18+1/2·(0,26·9,81/0,227)·0,2²+1/2·0,26·(0,02/0,0455)² = 0,459+0,225+0,025 = 0,709
• Auf der Höhe 3 besitzt der Körper die kinetische Energie 0, weil dort der Umkehrpunkt der Schwingung ist.
  Auch die potenzielle Energie ist dort 0, weil der Nullpunkt auf das Niveau 3 gelegt wurde.
  Folglich ist nur die Spannenergie von 0 verschieden. Das s ist der Abstand zwischen den Ebenen 1 und 3, also 380mm=0,38m.
  Es folgt: E_gesamt3=1/2·D·s²=1/2·(m·g/s₀)·s²=1/2·(0,26·9,81/0,227)·0,38² = 0,811
• Die weiteren Messungen ergeben für 
• H3=300mm ; t=0,026s : Energie auf Ebene 4: E_gesamt4=0,8883
  Energie auf Ebene 3: E_gesamt3=1,0388
• H3=250mm ; t=0,0079s : Energie auf Ebene 4: E_gesamt4=1,7721
  Energie auf Ebene 3: E_gesamt3=1,2944
• Information: Bei genaueren Messungen würde sich ergeben, dass E_gesamt4=E_gesamt3 . Der Energieerhaltungssatz besagt, dass auf jeder Höhe die Gesamtenergie gleich groß ist.

• Simulation/Berechnung zur Energie bei der Schwingung einer Schraubenfeder.
  Es werden die potenzielle Energie, die kinetische Energie, die Spannenergie und die Gesamtenergie graphisch dargestellt.
  Frei gewählt werden können die angehängte Masse m, die dadurch bewirkte Auslenkung s₀ der Schraubenfeder, der Ortsfaktor g, die Anfangsauslenkung h0 und die Zeitdifferenz Δt zwischen 2 "Messzeiten".