Unterrichts-Einsichten - Schuljahr 2007/2008 - Mathematik Ma4-g
Integralrechnung
2007-10-15
- Besprechung der Hausaufgabe
- Einführung in die Problematik der Berechnung krummlinig begrenzter Figuren.
2007-10-19
2007-11-05
- Rückblick auf die Ergebnisse der letzten Stunde vor den Ferien (siehe Link zum 2007-10-19)
- Berechnung
des Flächeninhaltes zwischen Normalparabel und x-Achse im Bereich von
x=0 bis x=b (b ist eine Variable, in der letzten Stunde hatte diese
Variable den Wert 1).
Erweiterung des Arbeitsblattes zur Berechnung krummlinig begrenzter Flächen. - Erweiterung der Lösung auf den Fall: Fläche im Bereich zwischen x=a und x=b.
- Hausaufgabe: Fläche zwischen Normalparabel und x-Achse im Bereich zwischen x=-5 bis x=+7.
2007-11-06
- Abschluss der Flächenberechnung in Verbindung mit der Normalparabel.
Folgende Ergebnisse haben wir erhalten:- Fläche zwischen Normalparabel und x-Achse im Bereich von 0 bis 1:

- Fläche zwischen Normalparabel und x-Achse im Bereich von 0 bis b:

- Fläche zwischen Normalparabel und x-Achse im Bereich von a bis b:

- Setzt
man für b einfach die Variable x, so erhält man mit A(x) die Fläche im
Bereich von 0 bis x. A(x) nennt man dann Flächeninhaltsfunktion.
Bei der Normalparabel gilt:  .
. - Als nächstes haben wir die Funktion
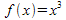 untersucht. Die Ergebnisse für die Flächeninhalte waren ganz ähnlich zu denen bei der Normalparabel.
untersucht. Die Ergebnisse für die Flächeninhalte waren ganz ähnlich zu denen bei der Normalparabel.
Man muss nur die Hochzahl 3 durch die Hochzahl 4 und den Nenner 3 durch den Nenner 4 austauschen. - Dieses Ergebnis und die Untersuchung der Funktionen
 und
und 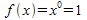 führten uns zu einer Vermutung, die durch folgende Tabelle wiedergegeben wird:
führten uns zu einer Vermutung, die durch folgende Tabelle wiedergegeben wird:

Die
Vermutung für die 3. Spalte war noch nicht ganz korrekt. Deshalb habe
ich einige Zellen frei gelassen. Nach der nächsten Mathestunde wird die
Tabelle weiter ausgefüllt.
Hausaufgabe: Lösung finden!
2007-11-09
- Die Tabelle haben wir vervollständigt zu

- Ihnen
fiel zwar die Gesetzmäßigkeit in der Tabelle auf, aber den
mathematischen Zusammenhang erkannten Sie noch nicht. Deshalb schloss
sich hier noch etwas Theorie an, die Sie hier nachlesen können.
- Am
Schluss der Doppelstunde haben wir erkannt: Die Aufgabe, ein Integral
zu berechnen, beinhaltet in der Hauptsache, eine Funktion zu finden
(ggf. zu erraten), deren Ableitung die gegebene Funktion ist. Behalten
Sie die Bemerkung in Erinnerung, die aus Ihren(!) Reihen kam: "Das ist
ja ganz einfach!"
2007-11-12

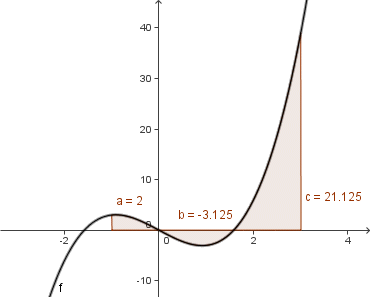
Gegeben war die Aufgabe, den Flächeninhalt der Fläche zu bestimmen, die zwischen dem Graph der Funktion mit der Gleichung  und der x-Achse im Bereich von x=-1 bis x=3 liegt.
und der x-Achse im Bereich von x=-1 bis x=3 liegt.- Das Integral von f(x) mit den Grenzen -1 und 3 ergibt den Wert 20:

Berechnet man aber die 3 Teilflächen, die jeweils von der Kurve und der x-Achse eingeschlossen werden, so ergibt sich 26,25.
Wir
haben gesehen, dass das daher kommt, dass das mittlere Flächenstück
unter der x-Achse liegt und bei der Berechnung einen negativen Wert hat.
Die Rechtecke der Ober- und Untersumme haben nämlich eine Höhe, die rechnerisch mit den Funktionswerten negativ ist.
Will man Flächeninhalte berechnen, so muss man also
1.
die gegebene Fläche aufteilen in Flächenstücke, die entweder
vollständig oberhalb oder unterhalb der x-Achse verlaufen (Nullstellen
bestimmen), dann muss man
2. die einzelnen Flächenstücke
berechnen, wobei bei den unter der x-Achse befindlichen Flächen der
Wert für den Flächeninhalt positiv genommen werden muss, und
3. addiert man zum Schluss alle erhaltenen Werte zusammen zum gesamten Flächeninhalt,
in diesem Beispiel also: 2 + 3,125 + 21,125 = 26,25 - Erkenntnis aus dieser Stunde: Man muss unterscheiden zwischen der Berechnung eines Integrals und der Berechnung eines Flächeninhaltes.
2007-11-13
- In dieser Stunde haben wir das Integrieren geübt und gesehen, wie man mit dem TI-84 Integrale bestimmen kann.
Zur Bedienung des TI-84 sei an die Anleitung im Bereich Materialien erinnert.
2007-11-16
- Zur Erinnerung:
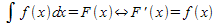
- Mit Hilfe dieser Beziehung lässt sich folgende Aufgabe leicht lösen:
Berechnen Sie die Fläche, die von der Sinuskurve und der x-Achse zwischen x=0 und x=π vollkommen eingeschlossen wird.
Der Taschenrechner liefert als Ergebnis den Wert 2:

Kann das sein? Ein so "glattes" Ergebnis?
Gesucht ist das Ergebnis für 
Also ist eine Funktion gesucht, die abgeleitet sin(x) ergibt. Lösung: -cos(x)
Daraus folgt: 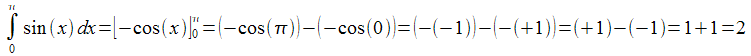
- Probleme gab es in der Stunde mit dem Winkelmaß.
Es gibt das "Winkelmaß" DEGREE und das Bogenmaß "RADIAN".
Winkelangaben mit DEGREE erfolgen in der Einheit "Grad", also z. B. α=180°,
Winkelangaben mit RADIAN erfolgen als reine Zahl, häufig als Vielfache von π, z. B. α=π
Die Umrechnung zwischen diesen beiden Winkelmaßen erfolgt so:
Bei RADIAN wird statt des Winkels in Grad die Länge des Kreisbogens des Einheitskreises genommen, die dem Winkel entspricht. - Wer unsicher im Umgang mit sin, cos und tan ist, sollte sich diese interaktive Animation ansehen (sehenswert!).
- Wir
haben einen ersten Einblick in das graphische Integrieren genommen
(geht ähnlich wie beim graphischen Differenzieren). Dazu aber in der
nächsten Stunde mehr.
2007-11-20
- Lösungen der Hausaufgabe (bitte unbedingt selbst noch einmal durchrechnen!)
- Hausaufgabe zur nächsten Stunde: Seite 246 Aufgabe 8
2007-11-23
- Der Theorieteil des laufenden Unterrichts ist nun komplett auf meiner Seite unter "Materialien" zu finden.
- Hausaufgabe: Seite 258 Aufgaben 7a und b, Fläche zwischen f(x)=x^2-4 und g(x)=x+1
2007-11-26
- Lösung der Hausaufgabe (Seite 258 Aufgabe 7b).
- Günstig ist bei der Berechnung von Flächeninhalten mit Hilfe der Intergralrechnung folgendes Vorgehen:
- Berechnung der Schnittpunkte der beteiligten Kurven oder der Kurve mit der x-Achse.
- Bestimmen der Stammfunktion
- Berechnung der positiv- und/oder negativ-orientierten Flächeninhalte.
- Berechnung des gesamten Flächeninhaltes aus dem Betrag der orientierten Flächeninhalte
- Bitte berichtigen Sie Ihre Hausaufgaben, damit sie sich die richtigen
Lösungsschritte einüben und Routine für die Klausur erhalten.
2007-11-27
- Rechnet man ohne Nachzudenken die folgende Aufgabe aus
 ,
,
so ergibt sich -2. - Schaut
man sich den Graph der Funktion an, so sollte man unsicher werden, weil
die entsprechende Fläche unter der Kurve oberhalb der x-Achse liegt,
das Rechenergebnis aber negativ ist.
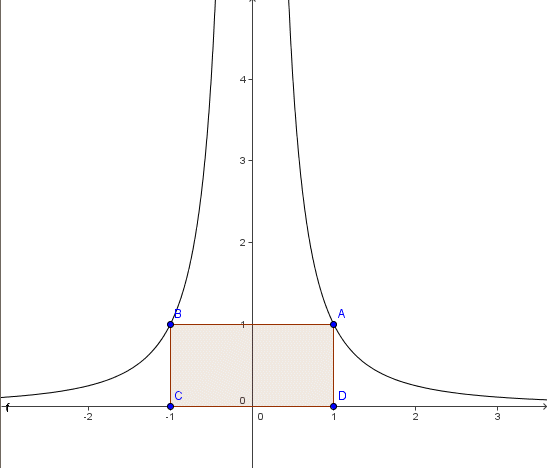
Außerdem
ist der Flächeninhalt des rot eingezeichneten Rechtecks schon 2. Die
Fläche zwischen Kurve und x-Achse reicht aber noch viel weiter in den
positiven y-RBereich hinein. - Taschenrechner und Geogebra geben beim Versuch der Berechnung des Integrals eine Fehlermeldung aus.
- Grund ist: Bei x=0 ist die Funktion nicht definiert (man kann nicht durch 0 dividieren).
- Dieses
Beispiel soll uns zeigen: Beim Integrieren muss die zu integrierende
Funktion für jeden x-Wert einen Funktionswert besitzen.
- Bei einem anderen Beispiel für die Berechnung des Flächeninhaltes einer unbegrenzten Fläche hatten wir mehr Glück:

Integrale mit einer Grenze, die über alle Schranken wächst (unendlich) nennt man "uneigentliche Integrale".
Interessant
ist, dass die Fläche des grünlichen Quadrates genau so groß ist wie die
nach rechts hin unbegrenzte rötliche Fläche zwischen Kurve und x-Achse:

2007-11-30
- Als Hausaufgabe sollten die Integrale
 und
und  berechnet werden. Es ergeben sich die Werte 1/2 und 1/3.
berechnet werden. Es ergeben sich die Werte 1/2 und 1/3.
Vermutungen
über Ergebnisse bei ähnlichen Integralen zeigten uns wieder einmal, wie
mächtig die Methode der Verallgemeinerung durch Einsatz von Parametern
statt Zahlen ist. 
- Man
sieht: Als Ergebnis ergibt sich immer ein Bruch mit einer 1 im Zähler
und mit einer Zahl im Nenner, die um 1 kleiner ist als der Exponent. im
Integranden.
- Es
schloss sich eine Wiederholung zu ganzrationalen Funktionen an.
Informationen zu diesem Stoff können Sie auf dieser Seite ab dem Datum
2007-09-14 nachlesen.
2007-12-03
- Wiederholung: Kurvendiskussion einer Kurvenschar mit der Gleichung
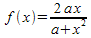 .
.
Hier 2 Kurven der Schar. Aufgabe zur Übung: Zu welchem a-Wert gehören die Kurven?


- Bitte unbedingt überlegen, was vor der Arbeit am Freitag noch zu fragen ist!
2007-12-04
- Wiederholung des Stoffs, der in der Klausur vorkommen wird.
- Ein weiteres Beispiel für die Kurvendiskussion einer Kurvenschar mit gebrochen-rationalen Funktionen (den ersten Teil haben wir schon im Unterricht besprochen).
2007-12-07
weiter mit Exponential- und Logarithmusfunktionen


 .
.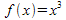 untersucht. Die Ergebnisse für die Flächeninhalte waren ganz ähnlich zu denen bei der Normalparabel.
untersucht. Die Ergebnisse für die Flächeninhalte waren ganz ähnlich zu denen bei der Normalparabel. und
und 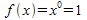 führten uns zu einer Vermutung, die durch folgende Tabelle wiedergegeben wird:
führten uns zu einer Vermutung, die durch folgende Tabelle wiedergegeben wird:



 und der x-Achse im Bereich von x=-1 bis x=3 liegt.
und der x-Achse im Bereich von x=-1 bis x=3 liegt.
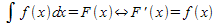


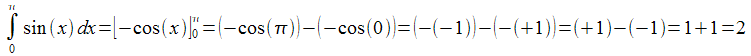
 ,
,


 und
und  berechnet werden. Es ergeben sich die Werte 1/2 und 1/3.
berechnet werden. Es ergeben sich die Werte 1/2 und 1/3.
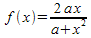 .
.
