Unterrichtseinsichten
- Schuljahr 2008/2009 - Mathematik 12MA1e
e-Funktion und natürlicher Logarithmus
2008-11-28
- Hier das Tafelbild mit den Überlegungen zum Problem y=y'. Genauere Ausführungen finden Sie hier.
2008-12-01
- Im Mittelpunkt der Stunde stand der Zusammenhang zwischen kontinuierlicher Verzinsung und Eulerscher Zahl e: Es gilt
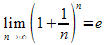(Beweis)
Genauere Ausführungen im Skript.
2008-12-03
- Wir haben die Funktion mit der Gleichung f(x)=x·ex untersucht.
Genauere Ausführungen finden Sie wieder im entsprechend erweiterten Skript.
2008-12-05
- Umkehrfunktionen und ihre Ableitungen (siehe Skript).
2008-12-08
- Allgemeine Exponentialfunktion und allgemeine Logarithmusfunktion (siehe Skript).
2008-12-10
- In
der Übungsstunde zur allgemeinen Logarithmusfunktion zeigte sich,
dass man die Logarithmengesetze kennen muss oder wenigstens wissen
muss, wo man sie finden kann (auf Seite 23 in der alten und auf Seite
12 in der neuen Formelsammlung). Bitte nachschlagen und wiederholen.
Schauen Sie doch auch mal hier in der Online-Formelsammlung nach!
2008-12-12
2008-12-15
- Lässt
man ein Stück eines Graphen um die x-Achse rotieren, so
ergibt sich ein Drehkörper, dessen Querschnitte alle Kreise sind.
Um
das Volumen eines solchen Körpers zu bestimmen, zerlegt man ihn in
flache Scheiben (Schnitt senkrecht zur x-Achse), die
näherungsweise die Form von Zylindern haben.
Deren Grundfläche ist die von Kreisen mit dem Radius r=f(x) und die Höhe ist ein differentiell kleiner Wert Δx.
Summiert man alle diese Volumina, ergibt sich für Δx gegen 0 das Gesamtvolumen: 
- Wir haben mehrere Körpervolumina mit diesem Integral berechnet:
- Zylinder: r ist Radius des Grundkreises, h die Höhe f(x)=r
- Kegel: r ist Radius des Grundkreises, h die Höhe f(x)=r/h·x
- Hausaufgabe: Volumen eines Kreises. Hilfestellung: Alle Punkte auf dem Kreis genügen der Koordinatengleichung x2+y2=r2.
weiter mit Stochastik