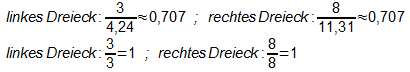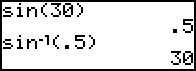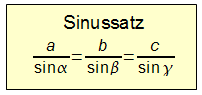Unterrichtseinsichten - Schuljahr 2012/2013 - Mathematik 9e
Trigonometrie
2013-01-09
- Wie haben unsere unterschiedlich großen Geodreiecke ausgemessen (persönliche Dreiecke und das Tafeldreieck:
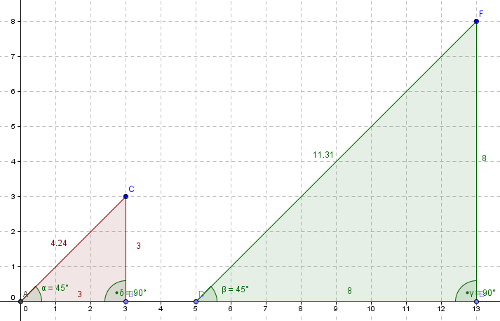
Da die Dreiecke ähnlich sind, sind die Winkel in beiden Dreiecken
gleich und auch das Verhältnis entsprechender Seiten ist gleich.
Beispiele: 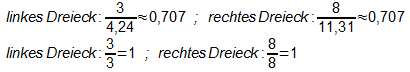
Anscheinden gehört die Winkelgröße 45° (die
übrigens auch in der oberen rechten Ecke gemessen wird) zu diesem
Verhältnis, denn wenn das Verhältnis sich ändert (so
haben wir jedenfalls ausprobiert), ändert sich auch der Winkel.
- Beim 2. Beispiel

habt ihr vermutet, der Winkel bei A im roten Dreieck habe den Wert
30° und der obere rechte Winkel den Wert 60° (also doppelt so
groß), weil die waagrechte Dreiecksseite doppelt so groß
wie die senkrechte Dreiecksseite sei.
Zur Überprüfung haben wir das Dreieck nach unten gespiegelt
(gelbes Dreieck). Es hätten dann alle Winkel im gesamten Dreieck
den Wert 60° und damit wäre das große Dreieck
gleichseitig. Da die senkrechte Seite im großen Dreieck die
Länge 10 (=2·5) hat, die schrägen Seitenaber
länger als 10 sind, kann die Annahme "30° und 60°" nicht
stimmen.
- Wir haben gesehen, dass bei verschiedenen rechtwinkligen
Dreiecken zu jedem Teilverhältnis von 2 Seiten des Dreiecks ein
ganz bestimmter Winkel gehört.
Nun stellte sich die Frage, wie man zu einem bestimmten Winkel das
entsprechende Teilverhältnis berechnen kann oder umgekehrt wie man
zu einem bestimmten Teilverhältnis den zugehörigen Winkel
berechnen kann.
- Bei
den folgenden Überlegungen benutzen wir einige spezielle
Bezeichnungen für die Seiten eines rechtwinkligen Dreiecks:
- Ein rechtwinkliges Dreieck hat 2 Katheten. Das sind die Seiten, die den rechten Winkel einschließen.
- Ist
ein Winkel (kleiner als 90°) im rechtwinkligen Dreieck festgelegt,
so nennt man die Kathete, die an diesem Winkel dran liegt die Ankathete
(AK).
Die Kathete, die dem Winkel gegenüberliegt, nennt man Gegenkathete (GK).
- Die 3. Seite nennt man Hypotenuse (HY). Sie liegt dem rechten Winkel gegenüber.
- Drei der möglichen Seitenverhältnisse haben einen bestimmten Namen bekommen, nämlich Sinus, Kosinus und Tangens:

- Zu jedem Winkel α erhält man mit sin α, cos α und tan α
das Verhältnis zweier Seiten eines rechtwinkligen Dreiecks.
Die
Bestimmung dieser Werte ist leider nicht einfach. Früher hat man
in jahrelanger Arbeit Listen mit Sinus-, Kosinus und Tangenswerten für alle
möglichen Winkel berechnet.
Heute
geht das mit dem Taschenrechner einfacher: SIN-Taste drücken und
dann den Winkel eingeben. Dabei darauf achten, dass unter MODE in der
3. Zeile DEGREE eingestellt ist.
Ebenso erhält man die Kosinus- und Tangenswerte mit der COS- und der TAN-Taste.
Aus
einem Verhältnis bekommt man den zugehörigen Winkel so: 2ND +
SIN drücken (analog 2ND + COS und 2ND + TAN), dann das
Verhältnis eingeben.
Beispiele:
sin 30° = 0,5 ; Taschenrechner: SIN(30)
30°
= arcsin 0,5 ; Taschenrechner: 2ND SIN(0.5) ;
arcsin wird Arkussinus gesprochen und auf dem Taschenrechner
durch sin-1 dargestellt.
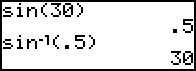
2013-01-14
- Wiederholung zur Definition der trigonometrischen Funktionen Sinus, Kosinus und Tangens (siehe oben).
- Während der Zensurenbesprechung Übungs- und Anwendungsaufgaben zu den trigonometrischen Funktionen in Gruppenarbeit.
2013-01-16
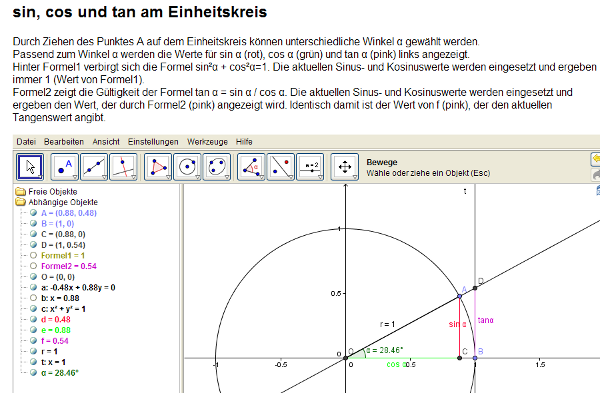
- Die Sinus-, Kosinus- und Tangenswerte kann man sehr gut am Einheitskreis (=Kreis mit dem Radius 1) ablesen:
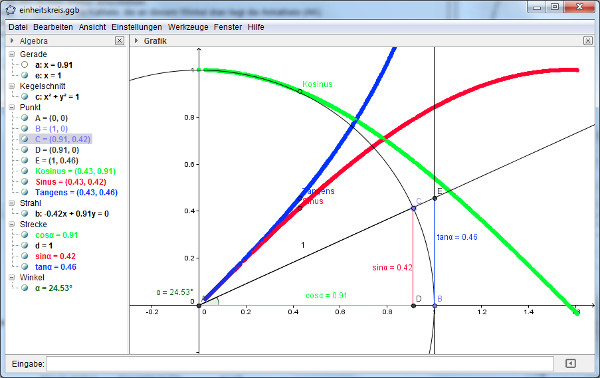
Im GeoGebra-Arbeitsblatt
kann man den Punkt C ziehen und damit den Winkel verändern.
Dargestellt werden die Werte für sin α (rote senkrechte Strecke),
cos α (waagrechte grüne Strecke) und tan α (senkrechte blaue
Strecke). Ein Klick auf das Bild oder den Link führt zum GeoGebra-Arbeitsblatt.
- Beim Ablesen der sin-, cos- und tan-Werte aus dem Einheitskreis in eurem Heft haben wir einige Besonderheiten gefunden:
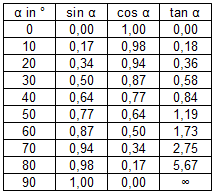
Die Werte von sin α und cos α sind gleich, aber von der Reihenfolge
entgegengesetzt aufgeschrieben. Es gilt sin α = cos (90°-α).
Die Werte für sin α und cos α liegen alle zwischen 0 und 1.
Tangenswerte sind immer größer oder gleich 0 und sind nach oben hin nicht begrenzt.
Für kleine α-Werte sind sin α und tan α fast gleich.
2013-01-23
- Die
meisten Sinuswerte lassen sich nicht durch einen kurzen Term angeben,
sondern müssen näherungsweise bestimmt werden oder aus
Tabellen oder mit dem Taschenrechner ermittelt werden.
Ausnahmen bilden u.a. die Sinuswerte für die Winkel 30°, 45° und 60°

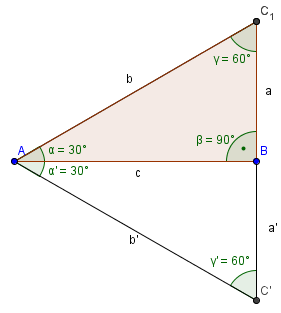
Im
roten rechtwinkligen Dreieck ist der Winkel α=30° gegeben.
Damit hat der dritte Winkel die Winkelgröße 60°.
Spiegelt man das Dreieck an der Seite c, so ergibt sich ein gleichseitiges Dreieck (alle Winkel 60°).
Es gilt sin α = a/b. Da a+a'=b, gilt b=2a.
Also folgt sin α = a/b = a/(2a) = 1/2.

Im
roten rechtwinkligen Dreieck ist der Winkel α=45° gegeben.
Damit hat der dritte Winkel auch die Winkelgröße 45°.
Das Dreieck ist also gleichschenklig und es gilt a=c.
b kann man nun mit dem Satz des Pythagoras berechnen: 
Damit gilt: 
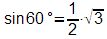

Im
roten rechtwinkligen Dreieck ist der Winkel α=60° gegeben.
Damit hat der dritte Winkel die Winkelgröße 30°.
Spiegelt man das Dreieck an der Seite a, so ergibt sich ein gleichseitiges Dreieck (alle Winkel 60°).
a ist die Höhe im gleichseitigen Dreieck, c ist halb so lang wie b, also b=2c.
Damit lässt sich a berechnen: 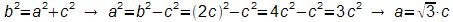
Damit gilt: 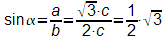
- Zusammenhang zwischen sin und cos

Es
gilt sinα=a/c und cosβ=a/c, also sinα=cosβ
mit β=90°-α, also sinα=cos(90°-α)
und sin(90°-α)=cosα.
- Zusammenhang zwischen sin, cos und tan
Es gilt 
- Tabelle mit sin-, cos- und tan-Werten für spezielle Winkel

oder zum besseren Merken nach Umformen einiger sin- und cos-Werte:

- Wiederholung zu den trigonometrischen Funktionen sin, cos und tan.
Siehe dazu auch das GeoGebra-Arbeitsblatt:
- Bei Aufgaben, die mit sin, cos und tan gelöst werden können, folgende Punkte beachten
- Wo finde ich rechtwinklige Dreiecke?
- Für sin, cos und tan benötige ich 2 Seiten und einen Winkel.
- Welche
Funktion haben die beiden Seiten im Dreieck? (Katheten oder Hypotenuse?
Ankathete oder Gegenkathete?) Welche Winkelfunktion passt dazu (sin,
cos, tan).
- sin-, cos- oder tan-Beziehung aufschreiben und nach der gesuchten Größe auflösen.
- Die Aufgabe mit der Prozentangabe für die Steigung lässt sich so sehr einfach lösen:

6%
Steigung bedeutet, dass eine Rampe oder Straße nach einer
waagrechten Ausdehnung von 100 (beliebige Längeneinheit) eine
Höhe von 6 aufweist.
Man kann also einfach rechnen: 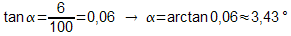
2013-01-28
- Erweiterung des Winkelbereichs für sin, cos und tan auf das Intervall [0°;360°].
Siehe dazu diese GeoGebra-Datei.
- Zum
Berechnen von Größen in beliebigen (also
nicht-rechtwinkligen) Dreiecken sucht man sich Teildreiecke, die
rechtwinklig sind.
2013-02-08
- Berechnungen an beliebigen Dreiecken
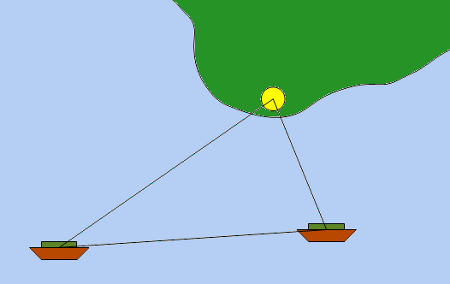
Ein Schiff fährt von links nach rechts an einer Landzunge vorbei.
Links sieht man den Leuchtturm unter dem Winkel α=36°, rechts unter dem Winkel β=68°.
Der Weg von der linken bis zur rechten Position beträgt 9km.
Wie weit ist das Schiff rechts vom Leuchtturm entfernt?
Lösung:
Planfigur: 
c=9 ; α=36° ; β=68°
Zunächst wird im Dreieck ABD die Länge von hc berechnet.
γ
ist der Ergänzungs winkel von α und β zu
180°: γ=180°-α-β=180°-36°-68°=76°
Im Dreieck BCD wird dann mit Hilfe von γ und hc die Seitenlänge von a bestimmt.
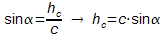
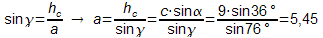
Das Schiff ist am Ort B also rund 5,5km vom Leuchtturm bei C entfernt.
- Die gefundene Formel lässt sich umschreiben nach
 .
.
Da
keine speziellen Werte enthalten sind und das Dreieck ohne
besondere Eigenschaften ist, ist das Ergebnis auch auf b und
sin β erweiterbar.
Diese Gesetzmäßigkeit nennt man Sinussatz:
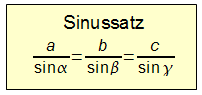
- Anmerkung: Beim stumpfwinkligen Dreieck liegt die verwendete Höhe außerhalb des Dreiecks.
Man
erhält dann statt sin α möglicherweise sin
(180°-α), statt sin β möglicherweise sin
(180°-β) und statt sin γ möglicherweise
sin (180°-γ).
Da aber sin α = sin (180°-α) für jeden Winkel α, ändert sich am Sinussatz nichts.
- Wie berechnet man die anderen Stücke in einem Dreieck, wenn
ein Winkel (hier α) und die beiden angrenzenden Seiten (hier b und c)
bekannt sind?
Einzeichnen von Hilfslinien: 
Rechnung:
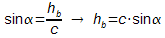


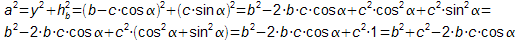

- Da wir nicht mit speziellen Werten sondern allgemein mit Buchstaben gerechnet haben, können wir das Zwischenergebnis a2=b2+c2-2·a·b·cos(α) verallgemeinern:
Wenn
in einem Dreieck 2 Seiten und der eingeschlossene Winkel bekannt sind,
kann man das Quadrat der 3. Seite berechnen nach folgender Formel:

- Anmerkung:
Der Satz des Pythagoras ist ein Spezialfall des Kosinussatzes: Ist
einer der Winkel α, β oder γ gleich 90°, so
fällt der letzte Summand im Kosinussatz weg und der Satz des
Pythagoras bleibt stehen.
2013-02-15
- Wiederholung zur Arbeit
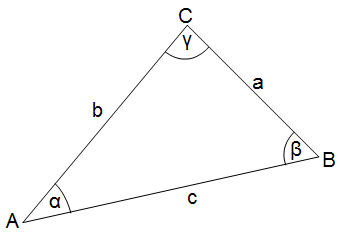
- rechtwinklige Dreiecke
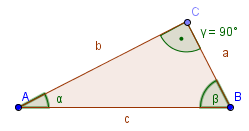

- allgemeine Dreiecke

Sinussatz: 
Man sollte die Formel nehmen, bei der die gesuchte Größe im Zähler steht, weil dann die Rechnung einfacher wird.
Den Sinussatz kann man benutzen, wenn 2 Winkel und deren gegenüberliegende Seiten gegeben oder gesucht sind.
Vorsicht: Beim Sinussatz können sich als Lösung 2 verschiedene Winkel ergeben (siehe nächste Stunde)!
Kosinussatz: 
Den Kosinussatz kann man dann benutzen, wenn 1 Winkel und alle 3 Seiten gegeben oder gesucht sind.
- Die Tafelbilder dieser Stunde findet ihr bei Moodle.
2013-02-18
- Winkelberechnung mit dem Sinussatz
Gegeben sind von einem Dreieck a=5, c=7 und α=23°. Zu berechnen ist der Winkel γ.
Planfigur: 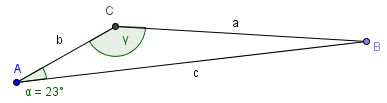
Anwendung des Sinussatzes: 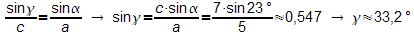
Dieser
Wert scheint nicht zu stimmen, da in der Zeichnung (Längen und
Winkelgrößen stimmen dort) ein Winkel >90° für
γ erwartet wird.
Die Lösung des scheinbaren Widerspruchs ergibt sich durch Konstruktion :
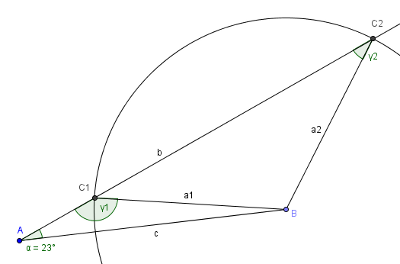
Hier
sieht man, dass es 2 Lösungen gibt: Die in der Rechnung gefundene
Lösung ist die Winkelgröße für γ2 rechts oben bei C2.
Am
Einheitskreis erkennt man, dass es zu einem bestimmten Sinuswert 2
verschiedene Winkel geben kann, die sich gegenseitig zu 180°
ergänzen:

Bei
der Berechnung von Winkeln mit dem Sinussatz muss man also immer
überprüfen, ob der Winkel größer als 90° oder
der Winkel kleiner als 90° der richtige Winkel ist.
In der Planfigur oben wäre also der Winkel 146,8° der richtige Winkel gewesen.
2013-02-19
- Letzte Wiederholung zur Klassenarbeit
- Tafelbild bei Moodle
2013-02-22
2013-03-01
weiter mit Figuren und Körper