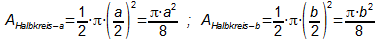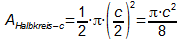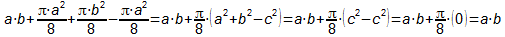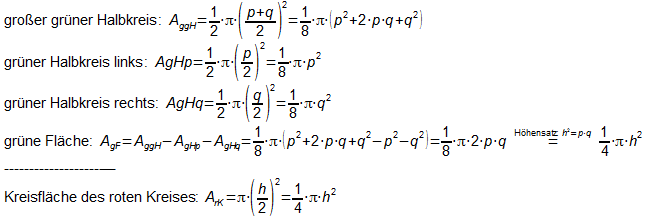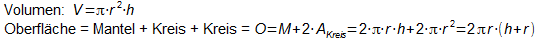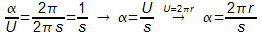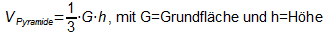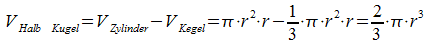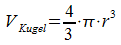Unterrichtseinsichten - Schuljahr 2012/2013 - Mathematik 9e
Figuren und Körper
2013-03-01
- Mehrere Beispiele brachten uns zum Problem: "Wie kann man den
Umfang eines Kreises berestimmen".
Erste Versuche: Anlegen eines Bindfadens oder einer Papierkante an den
Kreis, um dann die Länge zu messen:



Die Ergebnisse waren gar nicht schlecht: Für einen Kreis mit 5cm
Radius wurde ein Umfang zwischen 31cm und 32cm angegeben.
Wenn man es genauer haben will, muss man sich raffiniertere Methoden
ausdenken.
Vorschläge von Euch waren: Ein Dreieck oder Viereck in den Kreis
hineinlegen und dann den Umfang dieser Vielecke berechnen. Das Ergebnis
ist dann eine Näherung für den Kreisumfang, wird aber mit
Sicherheit einen zu kleinen Wert ergeben, da alle Teilstrecken
innerhalb des Kreises verlaufen. Betrachtet man nun auch noch Vielecke,
deren Seiten von außen am Kreis anliegen, so erhält man
wieder Näherungswerte, diesmal aber zu große Werte. Eine
Genauigkeitssteigerung erreicht man durch Vielecke mit sehr vielen
Ecken. Das wird dann Thema der nächsten Stunde sein.
2013-03-04
- Die Aufgabe dieser Stunde war: Bestimme zu einem Kreis mit
gegebenem Radius die Länge des Umfanges möglichst genau.
In der letzten Stunde haben wir schon durch Ausmessen gesehen, dass der
Umfang eines Kreises mit dem Radius 1 etwa 6,3 beträgt.
- Zu einer genaueren Abschätzung führt es, wenn man ein
Quadrat dem Kreis einbeschreibt und ein Quadrat umbeschreibt.
Die Umfänge der Quadrate geben dann ein Intervall an, das den
wahren Umfang des Kreises mit dem Radius 1 enthält.
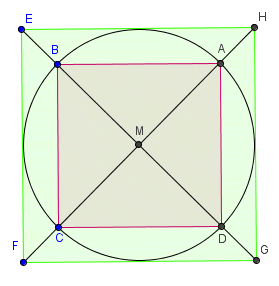
Da BM=1, folgt mit Hilfe des Satzes vom Pythagoras 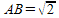 und damit für den gesamten Umfang des inneren
Quadrates:
und damit für den gesamten Umfang des inneren
Quadrates: 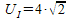 .
.
Die
Seitenlänge des äußeren Quadrates ist gleich dem
doppelten Kreisradius,
also 2. Der Umfang des äußeren Quadrates beträgt also 
Der wahre Wert des Kreisumfangs liegt also zwischen 5,6 und 8.
- Das
Intervall kann man verkleinern, indem man nicht ein Quadrat, also ein
regelmäßiges 4-Eck, sondern ein regelmäßiges
n-Eck benutzt mit einer
Zahl n>4.
AB
ist die Seitenlänge sn eines regelmäßigen n-Ecks. Die
Seitenzahl soll verdoppelt werden, so dass man ein 2n-Eck erhält.
Berechne
s2n mit der Annahme, dass sn bekannt ist. Es ist also eine Gleichung
s2n = . . . . sn . . . . gesucht, bei der auf der rechten Seite sn
vorkommt und bei der der Wert der rechten Seite die Seitenlänge
s2n
ergibt. Man sollte dabei bedenken, dass der Kreisradius 1 beträgt
und dass es den
Satz des Pythagoras gibt.
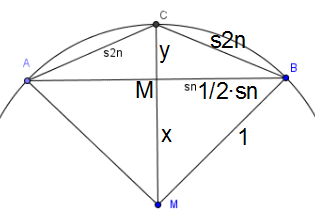
Lösung der Aufgabe:
Im rechten Teil der Figur finden sich 2 rechtwinklige Dreiecke, auf die
der Satz des Pythagoras angewendet werden kann:

Mit LibreOffice soll nun eine Näheruingsberechnung
durchgeführt werden. Dabei beginnen wir mit n=6 (Sechseck) und
gehen dann Zeile für Zeile weiter zum 12-Eck, 24-Eck, 48-Eck usw.
Die
Tabelle gibt uns mit wachsender Eckenzahl (scheinbar) immer genauere
Werte für den Kreisumfang des Kreises mit dem Radius 1:

In Zeile 26 erscheint aber unvermittelt (?) der Wert 0 für den
Umfang.
Was ist passiert?
Grund ist die eingeschränkte Rechengenauigkeit der
Tabellenkalkulation.
In der Formel 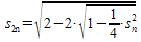 wird für großes n der Wert von sn
nahezu 0, damit die innere Wurzel fast zu 1 und unter der
äußeren Wurzel steht dann 2 - (fast)2, was fast 0 ergibt.
wird für großes n der Wert von sn
nahezu 0, damit die innere Wurzel fast zu 1 und unter der
äußeren Wurzel steht dann 2 - (fast)2, was fast 0 ergibt.
Irgendwann
kann dann der Rechner diesen kleinen Wert nicht mehr von "genau 0"
unterscheiden und bei der Multiplikation mit einer noch so großen
Zahl
n wird das Ergebnis zu 0.- Tritt bei Rechnungen ein solch katastrophaler Fehler auf wie in
der Tabelle ab Zeile 26, so spricht man von einer Subtraktions-Katastrophe, da der
Fehler dadurch bedingt wird, dass 2 etwa gleich große Zahlen
voneinander subtrahiert werden.
- Da
der Kreisumfang proportional zum Radius ist (Ähnlichkeit /
Stahlensätze) gilt für den Umfang U eines Kreises mit dem
Radius
r:
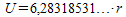 .
.
Als Abkürzung für die Hälfte der unhandlichen
Dezimalzahl hat man den griechischen Buchstaben pi (π) eingeführt,
so dass man schreiben kann: U=2·π·r
Die 2 steht da, weil man π definiert hat als den Quotienten aus U und
d, dem Durchmesser eines Kreises: U=π·d
- Es gibt viele
verschiedene Methoden, um den Wert der Zahl π zu ermitteln.
Hier ein Java-Applet, mit dem man die "Monte-Carlo-Methode" oder
"Regentropfen-Methode" ausprobieren kann.
Man lässt "Regentropfen" auf ein Quadrat der Seitenlänge r
fallen. Das Quadrat hat den Flächeninhalt r².
In dieses Quadrat wird ein Viertelkreis mit dem Radius r und dem
Flächeninhalt 1/4·π·r² eingezeichnet.
Das Verhältnis der beiden Flächeninhalte beträgt dann

Zählt man die Tropfen TK, die in den Viertelkreis gefallen sind
und dividiert diese Zahl durch die Anzahl aller Tropfen TA, so
erhält man näherungsweise dasselbe Ergebnis TK/TA=π/4.
2013-03-08
- Übungsaufgabe zur Kreisumfangsformel U=2·π·r
Neben der Satellitenaufgabe haben wir uns mit der Erdumfangsaufgabe
beschäftigt:
Angenommen, man hätte stramm um die Erde herum ein Seil gelegt,
sodass es überall dicht an der Erdoberfläche aufliegen
würde.
Nun wird das Seil um 1m verlängert und dann so gehalten, dass es
überall zur Erde den gleichen Abstand hat. Wie groß wird
dieser Abstand sein?
Merkwürdigerweise habt ihr denselben Abstand berechnet wie auch
später beim Ersetzen der Erde durch eine Pampelmuse und einen
Punkt.

Hier die allgemeine Rechnung zur Lösung der Aufgabe:


Unabhängig vom Radius U1 bleibt ein Abstand von fast 16
cm zwischen der Kugel und dem Seil.
- Flächeninhalt eines Kreises
Teilt man einen Kreis in gleiche "Tortenstücke" und ordnet man
diese so an wie in folgender Abbildung, kann man mit Hilfe des
Kreisumfangs sehr leicht auf den Flächeninhalt des Kreises
schließen:
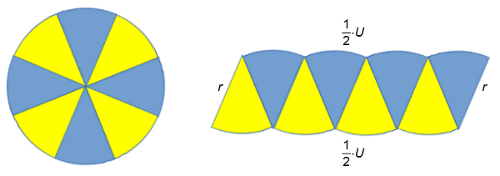
Es ergibt sich näherungsweise ein Parallelogramm mit den
Seitenlängen 1/2·U und r.
Dieses Parallelogramm wird immer mehr zu einem Rechteck, je schmaler
die "Tortenstücke" werden.
Im Grenzfall haben wir ein Rechteck mit den Seitenlängen
1/2·U und r. Als Flächeninhalt ergibt sich dann:

2013-03-15
2013-04-05
- Flächen- und Umfangsberechnungen
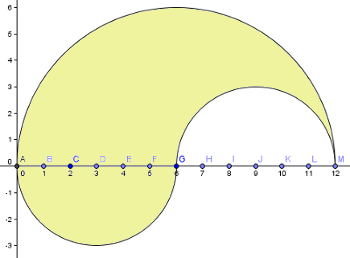


- Flächeninhalt
- Man sieht unmittelbar, dass in allen Zeichnungen die gelben
Flächen innerhalb der Figur gleich groß sind.
Die
kleinen nach unten gewölbten Halbkreise kann man nämlich in
die fehlenden weißen nach oben gekrümmten Halbkreise setzen
und es ergibt sich jedesmal ein Halbkreis mit dem Radius 6.
Auch bei
noch feineren Unterteilungen der x-Achse ergibt sich (wenn genau gleich
viele nach unten wie nach oben gerichtete Halbkreise existieren)
für die Flächeninhalte immer derselbe Wert.
Das gilt auch
für den Grenzfall, bei dem die kleinen Kreisbögen auf der
x-Achse nur als waagrechte Strecke zu erkennen sind.
- Umfang
- In
der linken Figur wird der Umfang der Figur gebildet aus dem Kreisbogen
für einen großen Halbkreis (Radius 6) und einem ganzen
Kreisumfang für einen Kreis mit dem Radius 3:

- In der mittleren Figur wird der Umfang der Figur gebildet aus
dem Kreisbogen für einen großen
Halbkreis (Radius 6) und 2 ganzen Kreisumfängen für einen
Kreis mit
dem Radius 1,5:

- In der rechten Figur wird der Umfang der Figur gebildet aus dem
Kreisbogen für einen großen
Halbkreis (Radius 6) und 3 ganzen Kreisumfängen für einen
Kreis mit
dem Radius 1:

- Das Ergebnis ist immer der Umfang eines groeßen Kreises
mit dem Radius 6.
Das
gilt auch für den Grenzfall, bei dem die kleinen Kreisbögen
auf der x-Achse optisch nicht von einer Strecke zu unterscheiden sind.
Der Umfang eines großen Halbkreises würde aber nur 6π+12
betragen.
- Arbelos (Schustermesser) oder Sichel des Archimedes
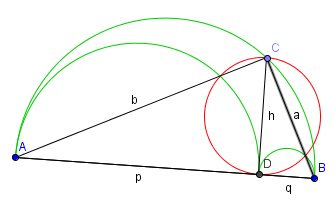
Aufgabe:
Die Flächeninhalte des roten Kreises und der grün umrandeten
Fläche sind zu vergleichen.
Lösung:
Idee: Die grün umrandete Fläche findet man, indem man vom
größten grünen Halbkreis die beiden kleinen grünen
Halbkreise entfernt.
Die Radien der Halbkreise sind immer halb so lang wie die Durchmesser
der Kreise.
Mit p+q=c gilt a²+b²=c²=(p+q)², weil bei C ein
90°-Winkel ist (Satz des Thales).
Rechnung:
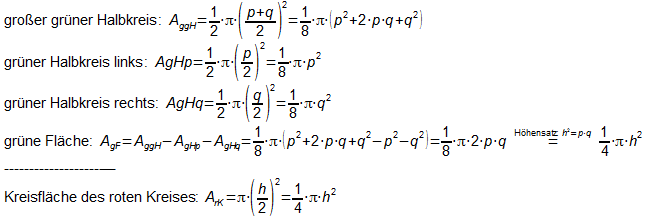
Man sieht, dass die Fläche des roten Kreises genau so groß
ist wie die grün umrandete Fläche, unabhängig von der
Lange des Punktes C auf dem Kreisbogen.
- Mit diesem Java-Programm
kann man durch Verändern des Punktes auf dem Kreisbogen sehen,
dass diese Beziehung besteht:
2013-04-05
- Mit Hilfe des Dreisatzes lassen sich sehr einfach die Formeln
für einen Kreisausschnitt finden:
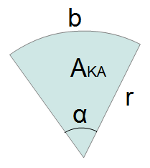
Flächeninhalt eines Kreisausschnittes: 
Bogenlänge eines Kreisausschnittes: 
2013-04-12
- Ein Zylinder ist von von 2 Kreisen und dem Mantel begrenzt.
Die Größe des Mantels lässt sich leicht berechnen, wenn man den Mantel zu einem Rechteck ausrollt.
Formeln für den Zylinder:
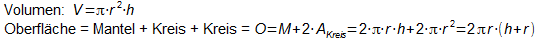


- Berechnung der Länge von Spiralen
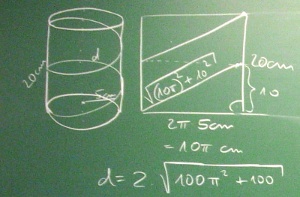
Man denkt sich die Spirallinie auf den Mantel eines Zylinders
gemalt, schneidet dann die Mantelfläche auf und rollt sie ab.
Die Spirallinie ergibt dann gerade aber schräge Strecken auf der
Mantelfläche.
Ist die Spirale n mal gedreht, so ergeben sich n Strecken.
Diese Streckenlängen können mit dem Satz des Pythagoras leicht
berechnet werden.
2013-04-19
- Besprechung der Hausaufgabe (Tafelbild bei Moodle)
- Während der Notenbesprechung Stillarbeit zum Thema Oberfläche bei Pyramiden und Kegeln.
2013-04-26
- In Verbindung mit der Berechnung von Oberflächen von Pyramiden haben wir folgende wichtigen Erkenntnisse gewonnen:
- Erst eine Zeichung der Figur als Schrägbild.
- Alle Eckpunkte, Strecken und andere wichtigen Dinge benennen.
- Teilflächen als eigenständige Zeichnungen zeichnen.
- Möglichst rechtwinklige Teildreiecke wählen, da dann mit dem Satz des Pythagors gerechnet werden kann.
- Kegelmantel

- Schneidet man den Mantel des Kegels an der Seitenkante s auf
und wickelt ihn ab, so ergibt sich ein Kreisausschnitt.
- Der Bogen U des Kreisausschnitts entspricht dem Umfang U der
Grundfläche des Kegels und der Radius s des Kreisausschnitts ist
gleich der Seitenkante s des Kegels.
Vergleicht man den Kreisbogen U mit dem Umgfang des gesamten
Kreises mit dem Radius s, so ergibt sich folgende
Verhältnisgleichung:
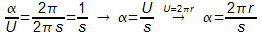
Vergleicht man nun den Mantel des Kegels, also den
Kreisausschnitt, mit der Fläche des gesamten Kreises, ergibt
sich:


2013-04-29
- Prinzip von Cavalieri
Sind in einem Körper die Querschnittsflächen in jeder
Höhe gleich, so sind die Volumina der Körper auch gleich.

Die Grundflächen der beiden Hohlkörper sind gleich (ca. 50 cm²).
Auf jeder Höhe sind wieder die gleichen Querschnittsflächen anzutreffen.
Die Volumina der beiden Hohlkörper stimmen also überein, wie wir beim Umfüllen mit Wasser erkennen konnten.
Es war beeindruckend, wie der bis zum Rand gefüllte Körper
links beim Umfüllen den rechten Körper (Zylinder)wieder bis zum Rand füllte.
- Volumen einer Pyramide
Drei gleiche Pyramiden passen genau in einen Würfel:


Da die Grundflächen von den Pyramiden und dem Würfel und auch
die Höhen überienstimmen, muss das Volumen der Pyramiden ein
Drittel des Würfel-Volumens sein:

Auch bei Pyramiden, die keine quadratischen Grundflächen haben und
bei denen die Höhe nicht gleich der Kante der Grundfläche
ist, kann man diese Gesetzmäßigkeit sehen:


Die 3 Pyramiden stimmen in der Grundfläche und der Höhe überein.
Sie passen zusammen genau in das gerade Prisma, das dieselbe
Grundfläche und die gleiche Höhe wie 2 der Pyramiden besitzt.
Die 3 Pyramiden füllen das Prisma genau aus.
Daraus folgt folgende erweiterte Regel für das Volumen von Pyramiden:
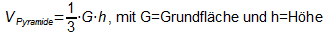
2013-05-03
- Kugelvolumen

Die Wasserspuren an den Körpern (Zylinder [Radius der
Grundfläche r und Höhe r gleich], Halbkugel [Radius r] und
Kegel [Radius der Grundfläche r und Höhe r gleich]) zeugen
vom Versuch, durch Umfüllen das Volumen der Kugel (bzw. Halbkugel)
zu ermitteln.
Durch Vergleich der Wassermengen haben wir herausgefunden, dass, weil
in den Kegel 1/3 der Wassermenge des Zylinders passt, die Halbkugel 2/3
der Wasserenge des Zylinders fassen kann. Damit fasst dann die Kugel
4/3 vom Zylinder, also 4/3·π·r3.
- Rechnerische Herleitung des Kugelvolumens mit Hilfe einer erweiterten Abbildung aus einem Geogebra-Arbeitsblatt:

Von oben betrachtet ergibt sich links ein Kreis mit Radius x und rechts ein Ring mit dem Radius r und der Dicke k bzw. j.
Zu zeigen ist, dass die Flächeninhalte dieser Gebilde übereinstimmen.
Vorüberlegung:
links ist der Schnitt senkrecht zu h, d. h. das aus h, x und r gebildete Dreieck ist rechtwinklig
rechts
liegt ein Quadrat vor, da Breite und Höhe gleich 2r sind. Die
Diagonalen verlaufen also unter einem Winkel von 45° und es gilt: RS =
SK = h
- Kreis links: A = π · x2 mit x2 = r2 - h2, also A = π · (r2 - h2)
- Ring rechts: Der Außenradius ist r und der Innenradius h, die Fläche also A = π · r2 - π · h2 = π · (r2 - h2)
- Die beiden Flächeninhalte stimmen also überein.
Nach
dem Satz von Cavalieri sind dann auch das Volumen der Halb-Kugel und
das Volumen des Zylinders vermindert um das Volumen des Kegels gleich:
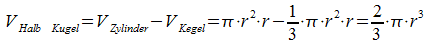
Das Volumen der ganzen Kugel beträgt also 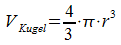
2013-05-17
- Versuch zur Berechnung der Kugeloberfläche
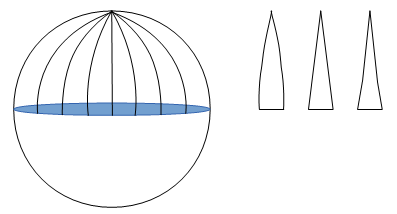
Ihr habt angeregt, die Kugeloberfläche wie eine Apfelsine
aufzuschneiden durch "gerade" Schnitte vom "Nordpol" bis zum
"Äquator".
Wir haben darüber diskutiert, wie diese Schnitte
flachgedrückt wohl aussehen würden und Ihr habt Euch mit
Mehrheit für das linke der 3 Auswahlstücke entschieden. Wir
konnten auch belegen, dass es nur diese Form sein kann, weil alle
Schnitte senkrecht auf den Äquator treffen.
Dann haben wir angenommen, die Fläche sei durch ein Dreieck
anzunähern, bei dem die Höhe dem Viertel eines Umfangs
entspricht:

Sämtliche Grundseiten zusammen ergeben den Kreisumfang des
Äquators, sodass die Fläche der oberen Kugelhälfte sichergibt aus

Die gesamte Kugeloberfläche wäre dann doppelt so groß, also π²·r².
In der Formelsammlung steht aber etwas anderes und außerdem kann
diese Näherung nicht richtig sein, weil die betrachteten Dreiecke
ja alle unten 2 rechte Winkel besitzen müssten, was aber wegen der
Winkelsumme 180° im Dreieck nicht geht.
Darum haben wir dann folgenden Versuch unternommen:
- Berechnung der Kugeloberfläche
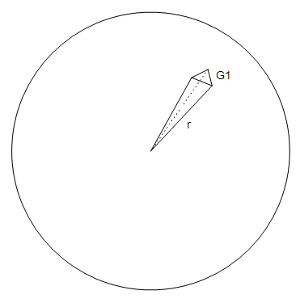
In
eine Kugel mit dem Radius r wird eine Pyramide so gelegt, dass die
Spitze der Pyramide im Mittelpunkt der Kugel und die Grundfläche
der Pyramide auf der Kugeloberfläche liegt.
Die
Kugeloberfläche ist zwar gekrümmt. Wenn man aber die
Grundfläche der Pyramide klein wählt, ist der Fehler
verschwindend gering.
Nun werden weitere Pyramiden auf gleiche Art
und Weise in die Kugel gelegt, bis das gesamte Kugelvolumen mit
Pyramiden ausgefüllt ist.
Die Summe der Pyramidenvolumina ist also gleich dem Kugelvolumen: 
Die Summe der Flächeninhalte der Pyramiden-Grundflächen ist gleich dem Inhalt der Oberfläche der Kugel: 
Also gilt: 
2013-05-27
- Wiederholung zur Klassenarbeit
Wichtig:
- Bei Textaufgaben immer erst eine Zeichung anfertigen.
- Bei 3-dim-Gebilden für zu berechnende Flächen oder Teilfiguren separate Zeichnungen erstellen.
- Möglichst allgemein (mit Buchstaben) rechnen und erst ganz zum Schluss gegebene Zahlenwerte einsetzen.
- π möglichst bis ganz zum Schluss stehen lassen: Vielleicht kürzt es sich ja heraus?
- Klammern sind kein Luxus, auf den man verzichten könnte!
2013-05-31
- Wiederholung zur Klassenarbeit
Die Tafelbilder sind bei Moodle zu finden.
2013-06-03
- Wiederholung zur Klassenarbeit
2013-06-07
2013-06-14
- Rückgabe der Klassenarbeit
- Einführung in das Arbeiten mit der 4-Feldertafel
- Soll
ein Sachverhalt untersucht werden, bei dem nach 2 Kriterien
unterschieden wird, die jeweils zutreffen können oder nicht
zutreffen können, so bietet sich als Hilfsmittel zur
Veranschaulichung eine 4-Felder-Tafel an:
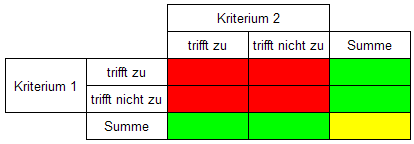
In
den roten Feldern steht, in welchem Maß die Kriterien 1 und 2
zutreffen, die grünen Felder enthalten die Summen der roten
Spalten- bzw. Zeilen-Felder, das gelbe Feld enthält die Summe der
roten Felder.
- Beispiel: In einer Umfrage werden die
Schülerinnen und Schüler der 9. Jahrgangsstufe befragt, ob
sie einen eigenen Computer besitzen, der höchstens 2 Jahre alt ist.
Die Darstellung der Ergebnisse der Umfrage erfolgt in einer 4-Feldertafel:
Kriterium 1: Junge oder Mädchen ; Kriterium 2: besitzt Computer oder besitzt keinen Computer.
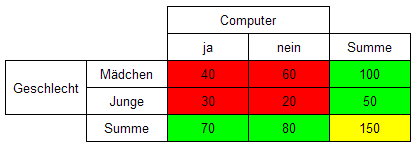
- Aus dieser Darstellung lassen sich nun leicht einige Aussagen ableiten:
- Fast
die Hälfte besitzt einen eigenen neueren Computer (die Summe 70
für "Computer -ja" ist nur geringfügig kleiner als die Summe
80 für "Computer - nein").
- 40% der Mädchen haben
einen eigenen Computer (insgesamt sind es 100 Mädchen, 40
Mädchen haben einen eigenen Computer, das sind 40%).
- Etwa
57% alle Computerbesitzer sind Mädchen (insgesamt gibt es 70
Computerbesitzer, darunter 40 Mädchen. Das ergibt 40/70=4/7 oder
etwa 0,57).
- Mehr Mädchen als Jungen besitzen einen
Computer (40 Mädchen aber nur 30 Jungen geben an, einen eigenen
Computer zu besitzen, also gibt es mehr Mädchen mit Computer.
Betrachtet man aber nicht die absoluten Zahlen sondern den jeweils
prozentualen Anteil, dann ergibt sich ein anderes Bild: 40% (40 von
100) der Mädchen und 60% (30 von 50) der Jungen besitzen einen
eigenen Computer, also gibt es prozentual mehr Jungen als Mädchen,
die einen eigenen Computer besitzen).
2013-06-18
- Zusammenhang zwischen Baumdiagrammen und 4-Felder-Tafeln
0,2% aller Bewohner eines Landes sind von einer bestimmten Krankheit betroffen.
Ein Test soll interessierten Personen zeigen, ob sie erkrankt oder gesund sind.
Man weiß, dass der Test bei 2% der gesunden getesteten Personen
positiv ausfällt, also auf die Krankheit hindeutet (falsch
positiv).
Man weiß, dass der Test bei 30% der kranken getesteten Personen negaitv
ausfällt, also auf Gesundheit hindeutet (falsch negativ).
1. Angenommen, der Test fällt positiv aus. Mit welcher Wahrscheinlichkeit ist man trotzdem gesund?
2. Angenommen, der Test fällt negativ aus. Mit welcher Wahrscheinlichkeit ist man trotzdem krank?

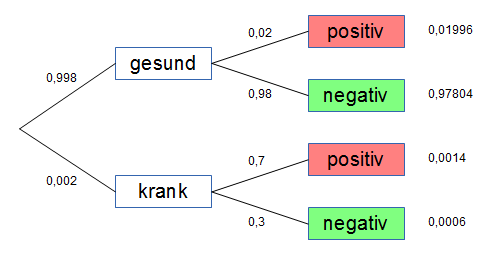
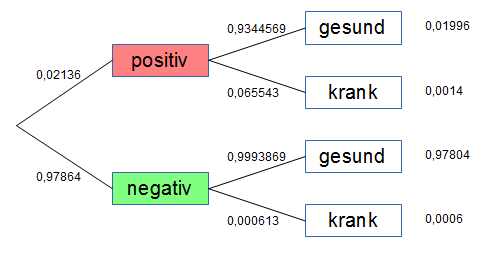
Antwort zu 1. : ppositiv(gesund)=93,4%
Antwort zu 2. : pnegativ(krank)=0,0613%




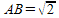 und damit für den gesamten Umfang des inneren
Quadrates:
und damit für den gesamten Umfang des inneren
Quadrates: 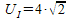 .
.



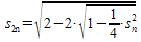 wird für großes n der Wert von sn
nahezu 0, damit die innere Wurzel fast zu 1 und unter der
äußeren Wurzel steht dann 2 - (fast)2, was fast 0 ergibt.
wird für großes n der Wert von sn
nahezu 0, damit die innere Wurzel fast zu 1 und unter der
äußeren Wurzel steht dann 2 - (fast)2, was fast 0 ergibt.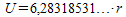 .
.