Unterrichtseinsichten - Schuljahr 2011/2012 - Mathematik 11ma3g

Analysis I

2011-08-30

Wiederholungen zur Differenzialrechnung

Die Steigung in einem Punkt P₀(x₀/f(x₀)) einer Kurve ist festgelegt als die Steigung der Tangente, die man an diesem Punkt an die Kurve anlegen kann.
Da Kurve und Tangente aber nur einen Punkt gemeinsam haben, wählt man zunächst einen weiteren Punkt P(x/f(x)) auf der Kurve und bestimmt die Steigung m_Sder Sekanten.
Dann lässt man den Hilfspunkt P auf der Kurve in Richtung auf P₀ gleiten und bestimmt jeweils die Sekantensteigung.
Als Grenzwert (P=P₀) ergibt sich aus der Sekantensteigung die Tangentensteigung m_T.
Entwicklung der Ableitungsformel:

Für m_T schreibt man auch f '(x₀) (1. Ableitung von f(x) an der Stelle x₀).
Beispielrechnung:
Steigung des Graphen von f(x)=x² an der Stelle x₀:
1. mit der (x-x₀)-Formel:

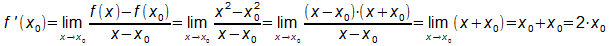
2. mit der h-Formel:
Wichtige Rechenregeln:

Einen Bruch kürzt man, indem man den gesamten Zähler und den gesamten Nenner durch dieselbe Zahl dividiert.
Binomische Formeln:
(a+b)²=a²+2ab+b² (a-b)²=a²-2ab+b² (a-b)(a+b)=a²-b²
Ableitungsregel: f(x)=xⁿ → f '(x)=n·x^n-1

2011-09-01

Einführung in GeoGebra
Beispiel: Von der Sekantensteigung über die Tangentensteigung zum Graphen der Ableitungsfunktion

Öffnen des Arbeitsblatts durch Klick auf den Link oder das Bild.
Zum Thema graphisches Differenzieren, das wir "per Hand" im Unterricht durchgeführt haben, gibt es dieses GeoGebra-Arbeitsblatt:
Die Bedeutung der ersten 3 Ableitungen wird in diesem GeoGebra-Arbeitsblatt untersucht:

2011-09-06

Die (Quadrat-)Wurzel aus einer positiven Zahl ist diejenige positive Zahl, die mit sich selbst multipliziert die Zahl unter der Wurzel ergibt.
Also: Eine Quadratwurzel hat immer einen positiven Wert!
Beispiel:
Eine quadratische Gleichung kann dagegen 2 Lösungen haben.
Man beachte dabei den meist ausgelassenen Zwischenschritt mit den Betragzeichen (in grün):
Lösen der Gleichung x²-9x=0

mit Hilfe der p-q-Formel:

So ist die Lösung sehr umständlich. Wenn q fehlt, sollte man die nächste oder übernächste Methode wählen.
Auflösen nach x:
Faktorisieren:

Einer der beiden Faktoren muss 0 sein:
1. Faktor ist 0: x₁=0
2. Faktor ist 0: x-9=0, also x₂=9

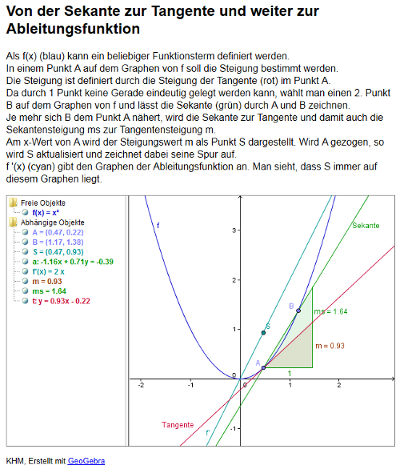
Wird ein Funktionsterm untersucht, bei dem die höchste Potenz von x größer als 3 ist, so müssen die Regeln für die Überprüfung auf Extrempunkte und Wendepunkte erweitert werden:

Ein Graph besitzt an der Stelle x einen Hochpunkt, wenn die 1. Ableitung gleich 0 ist und (falls die weiteren Ableitungen gleich 0 sind) als erstes eine gerade Ableitung (4., 6., 8., usw.) ungleich 0 und kleiner als 0 ist.
Ein Graph besitzt an der Stelle x einen Tiefpunkt, wenn die 1. Ableitung gleich 0 ist und (falls die weiteren Ableitungen gleich 0 sind) als erstes eine gerade Ableitung (4., 6., 8., usw.) ungleich 0 und größer als 0 ist.
Ein Graph besitzt an der Stelle x einen Wendepunkt, wenn die 2. Ableitung gleich 0 ist und (falls die weiteren Ableitungen gleich 0 sind) als erstes eine ungerade Ableitung (5., 7., 9., usw.) ungleich 0 ist.

Hausaufgabe: Seite 29 Aufgabe 17

2011-09-08

Die Aufgabe, Stellen maximaler und minimaler Steigung im Intervall [0;2,5] der Funktion
f(x) = -0,2·x⁶+1,8·x⁵-6·x⁴+8,8·x³-4,8·x²+4 zu finden, war nicht auf "übliche" Weise zu lösen, weil eine Gleichung 4. Grades hätte berechnet werden müssen.
Die Ableitungen selbst waren kein Problem, wohl aber das Lösen der Gleichung f ' '(x)=0.
f '(x) = -1,2·x⁵+9·x⁴-24·x³+26,4·x²-9,6·x
f ' '(x) = -6·x⁴+36·x³-72·x²+52,8·x-9,6
1. Lösungsmethode: SOLVER-Funktion des GTR
Mit der Taste MATH erhält man den folgenden Bildschirm

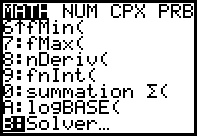
Falls nicht der Bildschirm mit der ersten Zeile EQUATION SOLVER sondern der nächste Bildschirm auftaucht, kann man mit "Cusor↑" zum richtigen Bildschirm wechseln.
Für x= wird ein Zahlenwert gesetzt, von dem aus die richtige Lösung gesucht wird. Beim ersten Suchen ist der Wert in den meisten Fällen beliebig.
Die Berechnung startet man mit ALPHA + ENTER

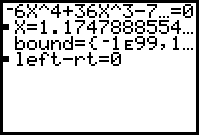
Es ergibt sich der Näherungswert x₁=1,1747888554 als erste Lösung für die Gleichung.
Weitere Lösungen erhält man ggf. durch andere Näherungswerte:

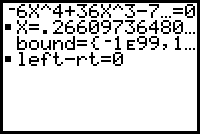
Mit dem Startwert x=0 erhält man eine 2. Lösung x₂=0,26609736480.
2. Lösungsmethode: MAXIMUM- und MINIMUM-Funktion von CALC
Die Ableitungsfunktion wird bei Y= eingegeben und deren Graph gezeichnet:

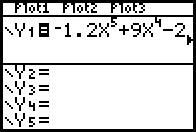
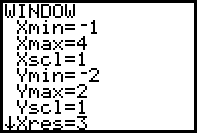
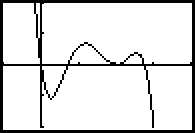
Mit 2ND + CALC gelangt man zu einem Menü, in dem man u.a. das Maximum und das Minimum eines Graphen suchen lassen kann.
Einzugeben sind die linke und die rechte Grenze des Suchbereichs sowie ein Startwert:


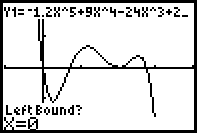
Die Lösung wird hier mit x=0,25509838 angegeben.
Auf gleiche Weise erhält man mit MAXIMUM die andere Lösung x=1,1747897
Man könnte statt der 1. Ableitung auch die 2. Ableitung eingeben und dann nach Nullstellen mit 2ND + CALC und ZERO suchen lassen.
Auch die Wertetabelle der 1. oder 2. Ableitungsfunktion könnte mit 2ND + TABLE benutzt werden, um maximale Werte oder 0 zu suchen.
Mit 2ND + TBLSET kann das Suchen in der Tabelle verfeinert werden (Abstände der x-Werte verkleinern).

2011-09-13

Beispiel für eine Steckbriefaufgabe:
Eine Funktion 3. Grades hat ihren Wendepunkt im Koordinatenursprung und besitzt einen Hochpunkt bei H(3/2). Gesucht ist die Funktionsgleichung.

1. Schritt:
Aufstellen der allgemeinen Funktionsgleichung und (weil Aussagen über den Wendepunkt gemacht werden), der 1. und 2. Ableitung.
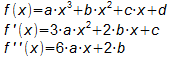
2. Schritt:
Bedingungen in mathematischer Schreibweise:
[1]: f ' '(0)=0 wegen Wendepunkt bei (0/0)
[2]: f (0)=0 wegen Punkt (0/0)
[3]: f (3)=2 wegen Punkt (3/2)
[4]: f '(3)=0 wegen Extrempunkt bei (3/2)
3. Schritt:
Einsetzen in die Funktionsgleichung und die Ableitungsfunktionen:
[1]: 0 + 2b = 0
[2]: 0 + 0 + 0 + d = 0
[3]: 27a + 9b + 3c + d = 2
[4]: 27a + 6b + c = 0
4. Schritt:
Vereinfachen:
Man sieht sofort, dass aus Gleichung [1] b=0 und aus Gleichung [2] d=0 folgt.
Damit vereinfachen sich die Gleichungen [3] und[4] zu
[3]: 27a + 3c = 2
[4]: 27a + c = 0
5. Schritt:
Lösen des Gleichungssystem (Gleichungen [3] und[4]):
[3]-[4] ergibt 2c=2. Daraus folgt c=1.
Eingesetzt in [4] ergibt sich 27a + 1 = 0 → 27a = -1 → a = - 1/27
6. Schritt:
Funktionsgleichung:

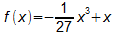
Bei Steckbriefaufgaben, aber auch bei vielen anderen Rechnungen, sind (lineare, d.h. Variablen kommen nur mit dem Exponenten 1 vor) Gleichungssysteme zu lösen.
Das Gaußsche Verfahren gibt einen Weg an, wie solche Gleichungssysteme immer gelöst werden können (wenn das auch nicht immer der einfachste Weg ist).
Beispiel für das Gaußsche Verfahren:

Aus der Gleichung [6] lässt sich unmittelbar z=3 ablesen; dieser Wert eingesetzt in Gleichung [4] ergibt den Wert -2 für y und beide Werte dann in Gleichung [1] eingesetzt ergeben den Wert -5 für a.
Es ist aber auch möglich, das Gleichungssystem noch weiter umzuformen:

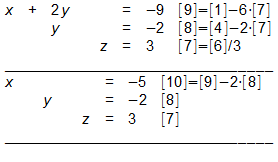
In dieser Form erkennt man sofort die Werte für x, y und z.
Lösung mit dem Taschenrechner:
Umformen des gegebenen Gleichungssystems. Dabei werden alle "überflüssigen" Elemente wie x, y, z, +, -, = weggelassen.
Mit dem rref-Befehl gibt der Taschenrechner dann die reduzierte Matrix an:
Hausaufgabe: Seite 33 Aufgabe 5f

2011-09-15

Gesucht war eine ganzrationale Funktion mit 2 Nullstellen bei x=-1 und x=+3 und einem Wendepunkt im Punkt (1/0), wobei die Steigung im Wendepunkt -4 betragen soll.

Zusammenstellung der Bedingungen:
f (-1) = 0 (Nullstelle)
f (+3) = 0   (Nullstelle)
f ' ' (1) = 0   (Wendepunkt bei x=1)
f (1) = 0   (Wendepunkt)
f ' (1) = -4   (Steigung im Wendepunkt)
Da 5 Bedingungen gegeben sind, wird mit einer Funktion 4. Grades gerechnet:
f (x) = a·x⁴ + b·x³ + c·x² + d·x + e
f ' (x) = 4·a·x³ + 3·b·x² + 2·c·x + d
f ' ' (x) = 12·a·x² + 6·b·x + 2·c
Aufstellen der Gleichungen entsprechend der oben genannten Bedingungen:
a - b + c - d + e = 0
81a + 27b + 9c + 3d + e = 0
12a + 6b + 2c = 0
a + b + c + d + e = 0
4a + 3b + 2c + d = -4
Eingabe der entsprechenden Matrix und Reduzierung mit dem rref-Befehl:
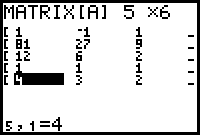
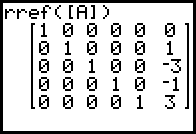
Auswertung:
Die berechnete Matrix ergibt: a=0, b=1, c=-3, d=-1, e=3 und damit f (x) = x³ - 3·x² - x + 3
"Merkwürdig" ist, dass mit a=0 die Funktion nicht wie vermutet 4. Grades, sondern nur vom Grad 3 ist.
Das Gleichungssystem ist also überbestimmt, d.h. es wird eine Bedingung/Gleichung zu viel gefordert.
Die überschüssige Bedingung ist aber zum Glück so angegeben, dass sie keinen Widerspruch zu den anderen Bedingungen ergibt.
Hätte man gleich mit einer Funktion 3. Grades gerechnet, so wäre der Rechengang folgendermaßen:
f (x) = a·x³ + b·x² + c·x + d
f ' (x) = 3·a·x² + 2·b·x + c
f ' ' (x) = 6·a·x + 2·b

-a + b - c + d = 0
27a + 9b + 3c + d = 0
6a + 2b = 0
a + b + c + d = 0
3a + 2b + c = -4

Auch hier ergibt sich f (x) = x³ - 3·x² - x + 3. Die letzte Zeile 0=0 ist immer wahr und hat damit keinen Einfluss auf die üpbrigen Gleichungen.

Würde eine Bedingung geändert, z.B. Nullstelle bei x=4 statt bei x=3, so hieße die 2. Gleichung 64a + 16b + 4c + d = 0 statt 27a + 9b + 3c + d = 0 und es ergäbe sich

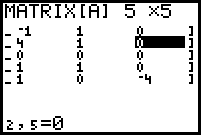
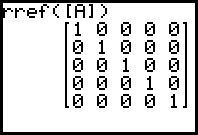
Die unterste Zeile bedeutet 0=1, es liegt also ein falsche Aussage vor. Das ganze Gleichungssystem hat keine Lösung.

2011-09-20

Fallunterscheidung beim Lösen von Gleichungssystemen
Bei den folgenden Beispielen wird angenommen, dass das Gleichungssystem jeweils mit dem Gaußverfahren oder mit dem rref-Befehl des Taschenrechners vereinfacht wurde.

Ergebnis
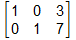
Das Gleichungssystem hatte 2 Gleichungen mit 2 Unbekannten.
Es gibt eine eindeutige Lösung: x=3 und y=7.
Ergebnis
Das Gleichungssystem hatte 3 Gleichungen mit 2 Unbekannten und war damit überbestimmt, d.h. eine Gleichung war überflüssig und es kann nur "durch Zufall" eine Lösung geben, wenn nämlich die Lösung, die sich aus 2 Gleichungen ergibt, auch bei der 3. Gleichung passt.
In diesem Fall ist es so, dass die Werte für die 2 Unbekannten in allen 3 Gleichungen eine richtige Aussage ergaben.
Die 3. Gleichung lautet nach der Umformung nämlich 0=0, ist richtig und hat damit keinen Einfluss auf die Lösbarkeit des Gleichungssystems.
Ergebnis
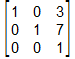
Auch dieses Gleichungssystem ist überbestimmt.
Hier steht in der 3. Gleichung aber 0=1, also eine falsche Aussage, die durch keine Wahl der Unbekannten richtig wird.
Das Gleichungssystem hat damit keine Lösung.
Ergebnis
Hier liegt ein Gleichungssystem mit 2 Gleichungen und 3 Unbekannten vor. Das Gleichungssystem ist unterbestimmt.
Es lassen sich nicht alle 3 Unbekannten aus den 2 Gleichungen ermitteln.
Ausgeschrieben sähe das Gleichungssystem so aus:
Man setzt nun z.B. für z einen Parameter ein (hier r) und gibt dann x und y in Abhängigkeit von r an:

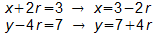
So ergeben sich die Lösungen x=3-2r, y=7+4r, z=r, wobei r eine beliebige Zahl aus dem Bereich der reellen Zahlen sein darf.
Es gibt also unendlich viele Lösungen.

2011-09-22

Bei einer Aufgabe zur Mischung eines Produkts aus 3 Komponenten ergab sich nach Aufstellen eines Gleichungssystems und der Vereinfachung mit dem Taschenrechner die Matrix .
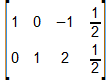Umformen ins Gleichungssystem, Ersetzen der 3. Vatriable durch r und Berechnung der Variabeln ergibt

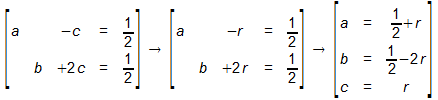
a, b und c geben die Anteile der Stoffe A, B und C an der Mischung an. Deshalb muss gelten 0<=a<=1, 0<=b<=1, 0<=c<=1.
Zu a: aus 1/2+r ≥ 0 folgt r ≥ -1/2, aus 1/2+r ≤ 1 folgt r ≤ 1/2.
Zu b: aus 1/2-2r ≥ 0 folgt r ≤ 1/4, aus 1/2-2r ≤ 1 folgt r ≥ -1/4.
Zu c: es gilt r ≥ 0 und r ≤ 1.
Da alle Bedingungen erfüllt sein müssen, gilt 0 ≤ r ≤ 1/4.
Daraus folgt 1/2 ≤ a ≤ 3/4, 0 ≤ b ≤ 1/2 und 0 ≤ c ≤ 1/4.
Berechnungen zum Verkehrsfluss an einer Kreuzung

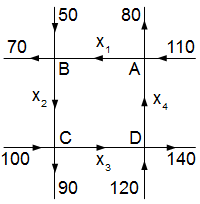
Der zu- und abfließende Verkehr an einer Kreuzung wird durch das Diagramm angegeben (Autos pro Zeiteinheit).
Die Werte für den inneren Kreuzungsbereich sollen berechnet werden.
Dazu wird an den Kreuzungspunkten A, B, C und D jeweils die Summe der zu- und abfließenden Fahrzeuge gezählt. Das Ergebnis muss 0 ergeben,
A: 110+x₄-80-x₁=0
B: x₁+50-70-x₂=0
C: 100+x₂-90-x₃=0
D: 120+x₃-140-x₄=0
Umformen, Matrix bilden, Matrix mit dem rref-Befehl vereinfachen, Umwandeln in Koordinatensystem, x₄=r setzen, x₁ bis x₄ berechnen:

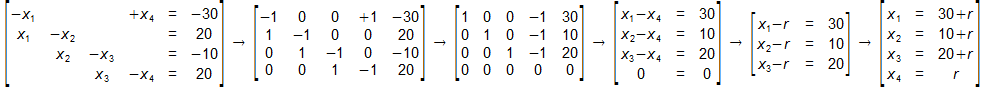
Erlaubte Werte für r berechnen: Wegen x₄=r gilt r ≥ 0. Nach oben hin gibt es für r keine Grenze.

2011-09-27

Besprechung der Hausaufgabe:
Gegeben ist ein Straßennetz aus Einbahnstraßen mit der Anzahl der Autos pro Zeiteinheit.
Gesucht sind die Auto-Durchflussraten in den Abschnitten x₁ bis x₇.

Für die Kreuzungspunkte von unten links nach unten rechts und dann von oben rechts nach oben links ergibt sich folgendes Gleichungssystem:

Es gibt unendlich viele Lösungen. r und s können im Prinzip beliebig gewählt werden. Beachtet werden muss aber, dass für alle i gelten muss x_i>=0.
Steht in der Aufgabenstellung "Eine 4-stellige Zahl ist gesucht...", so bezeichnet man die Zahl am besten durch 4 Buchstaben, z.B. abcd, wobei man aber darauf achten muss, dass a für die Tausender, b für die Hunderter, c für die Zehner und d für die Einer steht. Richtig dargestellt ist es also die Zahl 1000·a+100·b+10·c+d.
Hausaufgabe: Seite 44 Aufgabe 32 a und c

2011-09-29

Hinweis zur Hausaufgabe:
Wenn man ein Gleichungssystem aufstellen soll (z.B. bei Steckbriefaufgaben), muss man darauf achten, dass rechts von den Gleichheitszeichen nicht ausschließlich Nullen stehen.
Wenn links keine additive Konstanten vorkommen und rechts nur Nullen stehen, nennt man das Gleichungssystem homogen und dieses Gleichungssystem hat unendlich viele Lösungen.
In dem Fall könnte man nämlich jede Variable mit demselben Wert multiplizieren und da rechts immer 0 mal dieser Wert (also 0) steht, würde das Gleichungssystem auch diese neue Lösung haben.
Bei Steckbriefaufgaben kann es manchmal vorteilhaft sein, wenn man den Graph der gesuchten Funktionsgleichung im Koordinatensystem so verschiebt, dass man Funktionswerte oder Ableitungen bei x=0 liegen hat. Die Rechnungen werden dadurch möglicherweise sehr viel leichter. Anschließend muss man dann natürlich den Graphen wieder zurückverschieben durch entsprechende Änderungen in der Funktionsgleichung.
Themen für die Klausur

graphisches Differenzieren
Nullstellen (f(x)=0), Stellen mit waagrechter Tangente (f '(x)=0), Wendepunkte (f ' '(x)=0)
SOLVER, MINIMUM, MAXIMUM, ZERO usw. auf dem Taschenrechner
Steckbriefaufgaben in Worten oder mit gegebener Zeichnung
Gauss'sches Lösungsverfahren für Gleichungssysteme
Anzahl der Lösungen bei Gleichungssystemen / Fallunterscheidung
Aufgaben wie "Straßenkreuzung" oder "Zahlenrätsel"

2011-10-04

Klausur 1 [ Aufgaben | Lösungen ]

2011-10-06

Zum Thema "Kurvenanpassung" haben wir folgendes Beispiel betrachtet:

Die Gleise einer Moorbahn wurden von beiden Seiten eines Moorgebietes verlegt. Sie laufen parallel, sind aber 1m gegeneinander versetzt.
Als die Gleisenden noch 10m voneinender entfernt sind, beschließt man, ein gekrümmtes Übergangsstück einzusetzen, das so geformt ist, dass man den Übergang an den Nahtstellen bei A und B beim Überfahren nicht merkt. Die Funktionsgleichung des Übergangsstücks ist gesucht.

Wir haben gesehen, dass dazu die Funktionswerte der gesuchten Funktion und der Gleise bei A und B übereinstimmen müssen.
Ebenso müssen die Steigungen (also die 1. Ableitungen) bei A und B übereinstimmen.
Damit es nicht beim Übergang ruckelt, müssen die beiden 2. Ableitungen bei A und B gleich 0 sein.

Da 6 Bedingungen gegeben sind, muss man mit einer Funktionsgleichung 5. Grades arbeiten.
f(x)=a·x⁵+b·x⁴+c·x³+d·x²+e·x+f
f ' (x)=5a·x⁴+4b·x³+3c·x²+2d·x+e
f ' ' (x)=20a·x³+12b·x²+6c·x+2d
Das Koordinatensystem legt man günstig so, dass die Schienen parallel zur x-Achse laufen.
Die linke Schiene könnte z.B. auf der x-Achse liegen und der Endpunkt A könnte der Punkt (0/0) sein.
Dann hätte der Punkt B die Koordinaten (10/1).
Man könnte den Koordinatenursprung auch in den Punkt B oder in den Mittelpunkt der Strecke AB legen (der gesamte Graph wird nämlich symmetrisch sein).
Die Bedingungen und die dazu gehörenden Gleichungen:
f(0)=0 → f=0
f(10)=1 → 100000a+10000b+1000c+100d+10e+f=1
f ' (0)=0 → e=0
f ' (10)=0 → 50000a+4000b+300c+20d+e=0
f ' ' (0)=0 → d=0
f ' ' (10)=0 → 20000a+1200b+60c+2d=0
Nutzt man die schon jetzt vorhandenen Ergebnisse d=e=f=0 aus, so vereinfacht saich das Gleichungssystem zu einem System mit 3 Gleichungen:
100000a+10000b+1000c=1
50000a+4000b+300c=0
20000a+1200b+60c=0
Aufstellen der Matrix, Vereinfachen und Lösungen ablesen:

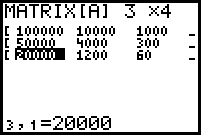
f(x)=0,00006·x⁵-0,0015·x⁴+0,01·x³
Kurvenverlauf (vorhandene Schienen in rot, Verbindungsstück in grün):

Die Sattelpunkte in A und B deuten darauf hin, dass der Übergang tatsächlich ohne zu ruckeln erfolgen wird.

Beim Anpassen von Funktionsgraphen mit Hilfe von Gleichungssystemen geht man günstig folgendermaßen vor:
1. Koordinatensystem geeignet festlegen
2. Bedingungen suchen
3. Gleichungssystem aufstellen
4. Lösung mit Gaußverfahren oder Taschenrechner berechnen
5. Lösung bewerten

2011-10-11

Kurvenschar und Ortskurve von Wendepunkten
Untersuchungsgegenstand war die Funktion f mit der Gleichung .
Das Ergebnis kann im folgenden GeoGebra-Arbeitsblatt erkundet werden:

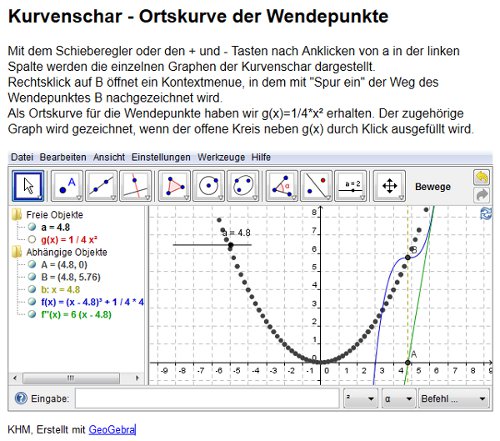
2011-10-13

Beispiel für die Anwendung einer Kurvenschar
Ein Hochspannungskabel soll in unwegbarem Gelände durch zwei 500m voneinander entfernte jeweils 30m hohe Masten A und B getragen werden.
Mast B ist 100m höher als Mast A.
Das Gelände ist fast eben, in der Nähe des Mastes B steigt es aber steil an.
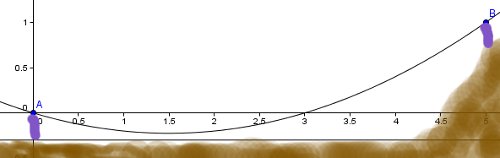
Mathematische Modellierung
Der Ursprung des Koordinatensystems wird in die Spitze des Mastes A gelegt.
1 Einheit entspricht 100m.
Die Funktionenschar mit der Gleichung f_t(x)=t·x²+(0,2-5·t)·x gebe angenähert den Verlauf des Kabels an.
Die Erdoberfläche wird durch die Gleichung g(x)=-0,3 beschrieben.
Welche Werte des Parameters t sind zulässig?
Eine Parabel 2. Grades ist nach oben geöffnet, wenn der Koeffizient vor x² positiv ist. t muss also positiv sein, da das Kabel nach unten druchhängt.
Wenn t=0, liegt eine Ursprungsgerade mit der Gleichung y=0,2·x vor:

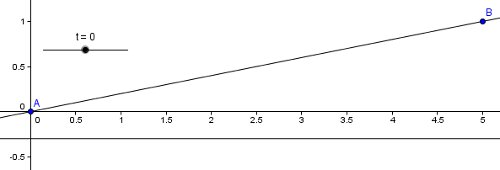
Durch Probieren findet man, dass t maximal den Wert 0,112 annimmt, weil sonst das Kabel auf dem Erdboden aufliegt:

Rechnerisch kann man diesen Wert ermitteln, indem man den Tiefpunkt in Abhängigkeit von t berechnet und dann die y-Koordinate -0,3 setzt (Turm A hat die Höhe 30m).

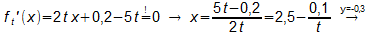
Der Wert t₁ entspricht dem oben ermittelten Wert, für den Wert t₂ liegt der Tiefpunkt symmetrrisch zur y-Achse im negativen x-Bereich und ist für die Aufgabenstellung deshalb nicht zu gebrauchen.

weiter mit Integralrechnung
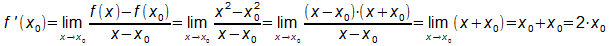
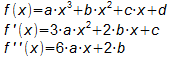
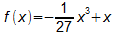
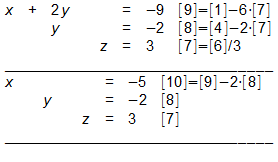
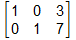
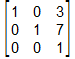
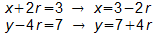
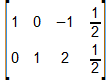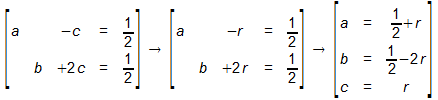
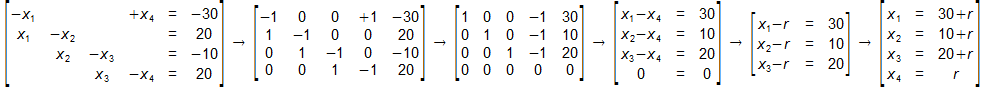