Unterrichtseinsichten - Schuljahr 2008/2009 - Mathematik 7d

Berechnungen an Vielecken und Prismen

• Aus einem breiten Pappstreifen sollen Einladungskarten geschnitten werden.
  Um nicht immer das "langweilige" Rechteck-Format zu benutzen, sollen die Karten eine Parallelogramm-Fläche erhalten.
  Braucht man mehr oder weniger oder gleich viel Pappe gegenüber dem Rechteckformat, wenn die Länge der Karte gleich bleibt?
  
  Bedingungen sind also: 
• waagrechte Seite immer gleich lang,
• schräge Seiten dürfen unterschiedliche Länge haben,
• gegenüberliegende Seiten müssen parallel sein,
• die Breite des Streifens, also die Höhen der Parallelogramme, müssen gleich sein.
• Zur Lösung der Frage haben wir zuerst die Anzahl der quadratischen Kästchen innerhalb der Parallelogramme gezählt.
  Ganze Quadrate sind gelb eingezeichnet, Teilfiguren, die sich zusammen zu einem Quadrat ergänzen, sind in gleicher Farbe dargestellt.
  
  links: 24 ganze Quadrate
  Mitte: 20 ganze Quadrate und 4 zusammengesetzte Quadrate ergeben 24 ganze Quadrate
  rechts: 16 ganze Quadrate und 8 zusammengesetzte Quadrate ergeben 24 ganze Quadrate.
  Folgerung: der Flächeninhalt bleibt gleich, ganz gleich wie schräg die Seitenkanten der Parallelogramme auch sind.
• Ihr habt dann auch herausgefunden, warum das so sein muss:
  "Wenn man an der einen Seite etwas wegschneidet, passt das genau an der anderen Seite".
• Schneidet man zum Beispiel bei der mittleren Figur das eingefärbte Dreieck rechts ab, kann man damit die Figur auf der linken Seite zu einem Rechteck ergänzen, das genau so groß ist wie das linke Rechteck:
  
• Bei der Figur rechts ist ein Schritt mehr notwendig:
  
• Es gilt also: Der Flächeninhalt eines Parallelogramms berechnet sich aus "Grundseite mal Höhe".
  Nachweis: Man kann ein Parallelogramm immer durch Verschieben von seitlichen Flächenstücken (parallel zur Grundseite) in ein Rechteck umformen, für das zur Berechnung des Flächeninhaltes gilt: "Grundseite mal Höhe".
• Überprüfung mit einem Parallelogramm, bei dem jede der Seiten einmal die Grundseite ist.
  Mit diesem GeoGebra-Arbeitsblatt kann man sich die Arbeit des Zeichnens und Rechnens abnehmen lassen:
  

• Die Aufgabe zum Ornament war anscheinend für Euch sehr schwer. Deshalb hier einige Tipps zur Lösung.
  Für die Hausaufgabe müsst Ihr mit anderen Werten rechnen (siehe Buch)!
  
• Die gelben Abschnitte sind Parallelogramme (das habt Ihr schon gefunden).
• Die Fläche eines Parallelogramms berechnet man durch "Grundseite mal Höhe".
• Elisa kam darauf, dass man einen Teil des Ornaments für sich betrachten kann, der auch ein Parallelogramm darstellt.
  
  Dieses Parallelogramm enthält 2 gelbe und 2 rote Flächenstücke.
  Mit den angegebenen Werten kann man nun die notwendigen Berechnungen durchführen.

• Besprechung der Hausaufgabe (siehe Aufgabe vom 2009-01-09)
• Flächenbestimmung bei einem Dreieck.
  Ihr habt gut das beim Parallelogramm Erlernte auf die Berechnung am Dreieck übertragen!
  Ein Dreieck mit der Grundseite a und der Höhe h_a besitzt den Flächeninhalt  A=1/2·a·h_a .
  Hier eine Auswahl der Zeichnungen, mit denen Ihr das Ergebnis gefunden habt:
   

• Besprechung der Hausaufgabe und weitere Übungen zur Flächenberechnung beim Dreieck.

• Flächenbestimmung bei einem Trapez (ein Trapez ist ein Viereck, bei dem mindestens 2 Seiten zueinander parallel sind)
  Eure Vorschläge zur Berechnung der Formel:
• 
  An das Trapez wird an einer Seite ein Dreieck mit der Grundseite a-c und der Höhe h angesetzt, sodass sich insgesamt ein Parallelogramm mit Grundseite a und Höhe h ergibt.
  Flächeninhalt des Parallelogramms minus Flächeninhalt des Dreiecks ergibt dann den Flächeninhalt des Trapezes:
  
• 
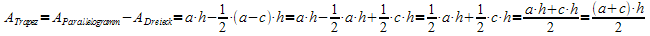
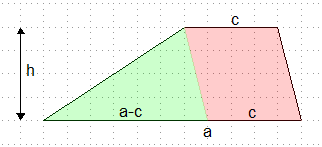
  Das Trapez wird aufgeteilt in ein Dreieck (grün) mit der Grundseite a-c und der Höhe h und in ein Parallelogramm (rot) mit der Grundseite c und der Höhe h.
  Die Summe aus dem Flächeninhalt des Dreiecks und dem Flächeninhalt des Parallelogramms ergibt den Flächeninhalt des Trapezes:
  
• 
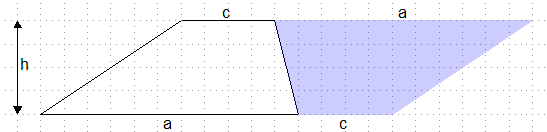
  Das Trapez wird um die Mitte der rechten schrägen Seite um 180° gedreht. Dann entsteht ein Parallelogramm mit der Grundseite a+c und der Höhe h.
  Nimmt man von diesem Parallelogramm die Hälfte des Flächeninhaltes, so erhält man den Flächeninhalt des Trapezes:
  
• ... und wie wäre es mit dieser Aufteilung des Trapezes?
   
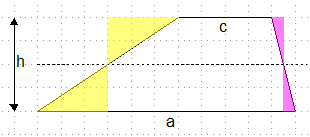
  Wie lang ist die Grundseite des entstehenden Rechteckes?

• Flächeninhalt eines Vieleckes
  
  Nach einigen Überlegungen habt Ihr mehrheitlich vorgeschlagen, das gegebene 5-Eck in 3 Dreiecke zu zerlegen und die Flächen dieser Dreiecke zu bestimmen.
  Eure Ergebnisse waren 25,58 ; 25,31 ; 25,47 ; 23,61 ; 24,76 ; 25,28 ; 26,50 ; 24,16 ; 24,84 ; 25,16. Hausaufgabe: Mittelwert berechnen.
• Haben wir mit dem Mittelwert den wahren Flächeninhalt?
  Die gegebenen Eckpunkt haben alle ganzzahlige Koordinaten. Ob man damit nicht auch einen exakten Wert berechnen kann, ohne sich auf ungenaue Messungen verlassen zu müssen?
  Dazu mehr in der nächsten Stunde.

• Als Mittelwert ergibt sich bei der Flächenbestimmung aus Euren Messwerten 25,07.
  Ist das der exakte Wert des Flächeninhalts? Wahrscheinlich nicht.
  Welches ist denn der exakte Wert? Vielleicht genau 25?
• Ein sehr einfaches Vorgehen zur Bestimmung des genauen Wertes haben wir heute kennen gelernt:
  Man umschließt das Vieleck durch ein Rechteck, berechnet den Flächeninhalt dieses Rechteckes und subtrahiert davon die Flächeninhalte der Flächen, die im Rechteck, aber nicht in der zu berechnenden Fläche sind:
  
  Flächeninhalt des Rechteckes (roter Rahmen): 8·6=48
  Flächeninhalt der einzelnen Flächen (grün): A1-->5,0 ; A2-->6,0 ; A3-->4,0 ; A4-->3,0 ; A5-->4,5 , zusammen 22,5
  Flächeninhalt des 5-Eckes (rötlich): 48 - 22,5 = 25,5
• Der Mittelwert Eurer Messungen bzw. Rechnungen war schon sehr gut!
  Ihr seht aber, dass man sich auf Messungen nicht unbedingt verlassen kann, auch wenn man mit mehreren zusammen misst und rechnet.
  Die Methode mit dem umgebenden Rechteck kann man auch auf alle möglichen anderen Flächen anwenden, die durch gerade Strecken begrenzt werden.

• Als Hausaufgabe war der Flächeninhalt des Dreiecks mit den Eckpunkten A(1/2), B(6/1) und C(4/7) zu berechnen.
  
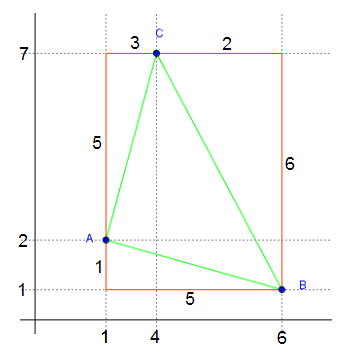
  An einer nicht maßstabsgerechten Zeichnung haben wir gesehen, dass man mit der Methode des "Um-Rechteckes" durch Rechnung ein exaktes Ergebnis erhalten kann:
• Flächeninhalt des Rechteckes: 5·6=30
• Flächeninhalt des Dreieckes links oben: 5·3/2=7,5
• Flächeninhalt des Dreieckes rechts oben: 6·2/2=6,0
• Flächeninhalt des Dreieckes unten: 5·1/2=2,5
• Gesamtflächeninhalt der äußeren Dreiecke: 7,5+6,0+2,5=16,0
• Flächeninhalt des grünen Dreieckes = Flächeninhalt des Rechteckes - Flächeninhalt aller äußeren Dreiecke = 30 - 16 = 14
  Durch Abmessen (Grundseite mal Höhe durch 2) auch bei sehr genau gezeichnetem grünen Dreieck haben viele von Euch nicht dieses exakte Ergebnis erhalten.

• Besprechung der Hausaufgabe
  Achtet beim Umformen von Einheiten darauf, ob Ihr eine einfache Einheit oder eine Einheit zum Quadrat habt.
  Beispiel: 1m = 100cm, aber 1m² = 10000cm², weil 1m² = 1m·1m = 100cm·100cm = 10000cm². 

• Flächeninhaltsbestimmungen bei Flächen mit gekrümmten Begrenzungen werden erst in der 11. und 12. Klassenstufe besprochen (Integralrechnung).
  Näherungsweise können wir aber solcher Flächeninhalte auch mit Hilfe der bekannten 3- und 4-Ecke abschätzen.
  Beispiel:
  
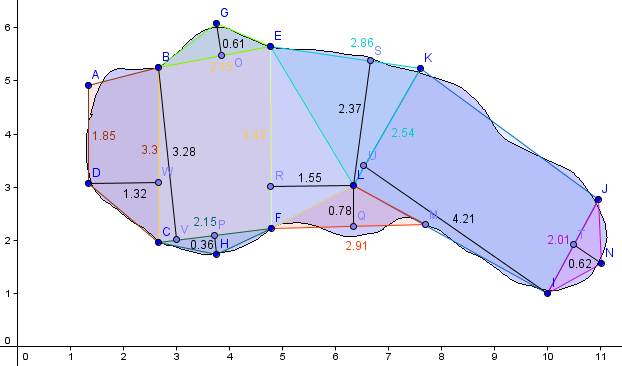
  Die Fläche eines Sees wird durch Dreiecke und Trapeze abgedeckt und die Flächeninhalte dieser Figuren werden berechnet:
• Trapez A_ABCD = (1,85+3,3)·1,32/2 = 3,399
• Trapez A_BCFE = (2,15+2,15)·3,28/2 = 7,052
• Dreieck A_BEG = 2,15·0,61/2 = 0,656 
• Dreieck A_CHF = 2,15·0,36/2 = 0,387
• Dreieck A_FLE = 3,43·1,55/2 = 2,658
• Dreieck A_ELK = 2,86·2,37/2 = 3,389
• Dreieck A_FML = 2,91·0,78/2 = 1,135
• Trapez A_LIJK = (2,54+2,01)·4,21/2 = 9,578
• Dreieck A_INJ = 2,01·0,62/2 = 0,623
• Gesamtfläche: 3,399+7,052+0,656+0,387+2,658+3,389+1,135+9,578+0,623 = 28,878
  Steht eine Einheit für die Länge 1km, so hat der See etwa eine Fläche von 28,88km² .

• Konstruktion von Schrägbildern.
  Vorgehensweise: Die Strecken, die senkrecht in die Papierebene hinein gezeichnet werden müssten und die deshalb (bis auf einen Punkt) nicht sichtbar wären, werden unter einem bestimmten Winkel schräg zu einer waagrechten Achse und um einen Faktor k verkürzt gezeichnet. Alle in der Zeichenebene liegenden Strecken werden genau ihren Maßen entsprechend gezeichnet.
• In folgender Abbildung wird das Dreieck ABC (links) um 90° nach hinten gekippt, so dass nur noch die Seite AB zu sehen sein würde.
  Stattdessen wird aber die Strecke PC (die nach dem Kippen senkrecht nach hinten verlaufen würde) unter einem Winkel von 30° zur Strecke AB und verkürzt (mit dem Streckfaktor 3/5) gezeichnet.
   
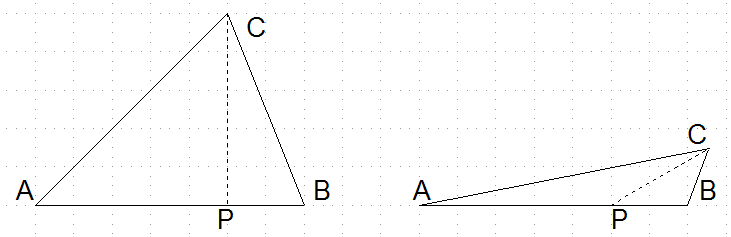
  Man sieht das rechte Dreieck so, als ob man von schräb rechts oben darauf blicken würde.
  Vergleiche die Tischplatte, die in Wirklichkeit quadratisch ist. Die rechte Kante ist verkürzt dargestellt. Auf Grund des seitlichen Abstandes ist der Winkel der linken Tischkante zur Waagrechten kleiner als der Winkel der rechten Tischkante. Bei unseren mathematischen Konstruktionen wählen wir alle Neigungswinkel gleich.

• Vereinfachtes Zeichnen eines Schrägbildes auf Kästchen-Papier
  
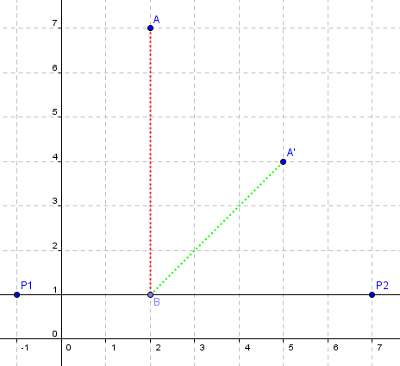
  Soll der Punkt A abgebildet werden, so wählt man zunächst eine waagrechte, auf dem Koordinatengitter verlaufende Grundlinie.
  Von A wird eine Senkrechte Strecke bis zur Grundlinie im Punkt B gezeichnet (rot).
  Von B aus wird diagonal (45° zur Grundlinie) ein Strahl gezeichnet.
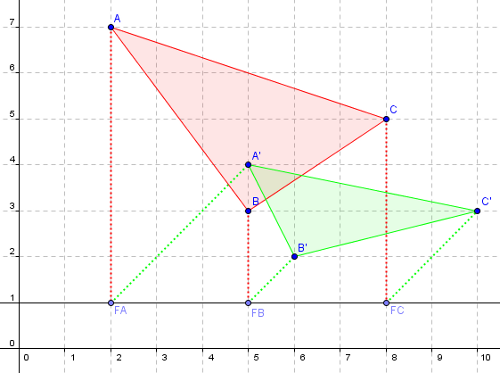
  Man misst aus, wie viel Kästchen Abstand die beiden Punkte A und B haben. A' und B haben dann einen Abstand, der der Hälfte dieser Kästchenzahl entspricht und in Quadrat-Diagonalen gemessen wird. In unserem Beispiel: Zwischen A und B befinden sich 6 Kästchen-Längen. Dann muss B von A' den Abstand "3-mal eine Kästchen-Diagonale" haben.
• Beispiel für das Schrägbild eines Dreiecks. Das rote Dreieck wird um 90° nach hinten geklappt. Dadurch würde man nur noch einen Strich sehen. Im Schrägbild dagegen kann man das Dreieck (grün) so sehen, als wenn von links oben eine Lampe durch das rote Dreieck scheinen würde und einen grünen Schatten auf der gedachten waagrechten Ebene bilden würde.
  
  
• Prismen sind Körper, die aus zwei kongruenten Flächen bestehen, die parallel zueinander liegen.
  Die entsprechenden Eckpunkte der beiden Flächen sind durch gleich lange, parallele Strecken miteinander verbunden.
  Beispiel:

• Besprechung der Hausaufgabe und weitere Übungen zum Berechnen der Volumina von Prismen (V=G·h).

• Besprechung der Hausaufgabe.
• Bei der Aufgabe zu den Parfum-Fläschchen haben wir gesehen, wie man den Taschenrechner geeignet zum Finden der Lösung einsetzen kann:
• Mit Stat>Edit wird der Listeneditor aufgerufen.
• In L1 werden die Parfum-Mengen jeder Packung eingetragen.
• In L2 werden die Packungs-Volumina eingegeben durch Länge·Breit·Höhe
• In L3 wird in der Kopfspalte L1/L2 eingegeben. Damit wird für alle Parfum-Packungen das Verhältnis von Parfum-Menge zu Packungsgröße berechnet.
  
• Werden die Listeninhalte von L1 und L2 so dargestellt, dass die L1-Werte auf der waagrechten und die L2-Werte auf der senkrechten Achse abgetragen werden, so ergibt sich
  
  Die Punkte geben das Verhältnis von Ware zu Verpackungsgröße an:
  Für 1, 2 oder 3 Packungen erhält man die 1-, 2- oder 3-fache Menge an Ware und an Verpackung.
  Ware und Verpackung für ein Produkt sind also proportional und entsprechende Punkte in der graphischen Darstellung liegen auf einer Ursprungsgerade:
  
  Für die Ware mit der flachsten Gerade gibt es am meisten Ware bezogen auf die Verpackungsgröße.

• Weitere Übungen zum Berechnen von Prismen-Volumina.
• Zur Erinnerung: Es ist manchmal einfacher, zu berechnende Flächen nicht aufzuteilen und dann die Inhalte der Teilflächen zu berechnen, sondern die zu berechnende Fläche in ein Rechteck zu bringen, dessen Flächeninhalt zu berechnen und dann die Inhalte der nicht vorhandenen Randflächen abzuziehen.
  Zum besseren Verständnis hier ein Beispiel aus dem Unterricht:
  
• Mehrere haben die gelbe Fläche so zerlegt, wie es durch die gestrichelten Linien angedeutet wird.
  Daraus ergaben sich folgende Berechnungsschritte:
• Rechteck ganz links: 5·6=30
• Rechteck in der linken Mitte: 4·4=16
• Dreieck in der linken Mitte: 1/2·4·2=4
• Rechteck ganz rechts: 5·6=30
• Rechteck in der rechten Mitte: 4·4=16
• Dreieck in der rechten Mitte: 1/2·4·2=4
• insgesamt ist der Flächeninhalt also 30+16+4+30+16+4=100
• multipliziert mit der Länge des Werkstücks ergibt sich 100·18=1800
• Durch die Symmetrie der gelben Fläche kann man die Rechnung natürlich erheblich vereinfachen.
• Andere Methode: Die gelbe Fläche zu einem Rechteck ergänzen und dann die Fläche des zu viel berechneten Dreiecks abziehen:
• Fläche Rechteck: 6·18=108
• Fläche Dreieck: 1/2·8·2=8
• Fläche Rechteck minus Fläche Dreieck: 108-8=100
• multipliziert mit der Länge des Werkstücks ergibt sich 100·18=1800

• Besprechung der umfangreichen Hausaufgabe / Aufgabe für die Vertretungsstunde

• Weitere Übungen zum behandelten Unterrichtsstoff.
• Zur Arbeit bitte die Seiten 127-128, 132-144, 146-158 wiederholen.
  Themen: 
• Einheiten und deren Umwandlung ineinander bei Flächeninhalten und Volumina.
• Flächeninhalte von Parallelogrammen, Dreiecken, Trapezen und Vielecken
• Konstruktion von Schrägbildern
• Oberflächen und Volumina von Prismen

• Wiederholung zur Arbeit (2009-02-23).

• Klassenarbeit 3   [ Augaben | Lösungen ]