Unterrichtseinsichten - Schuljahr 2008/2009 - Mathematik 7d

Mehrstufige Zufallsexperimente

• Auf dem Schulweg muss man über 3 Ampelkreuzungen gehen. Die Ampeln werden unabhängig voneinander geschaltet und haben unterschiedlich lange Rot- und Grünphasen.
  
  Was wird häufiger vorkommen: 3 grüne Ampeln hintereinander oder 3 rote Ampeln hintereinander?
  Ihr habt herausgefunden, dass häufiger 3 rote Ampeln hintereinander vorkommen werden, da die Rot-Phasen länger sind als die Grün-Phasen.
• Wie groß ist die Wahrscheinlichkeit, dass die 1. Ampel Grün zeigt, wenn man dort ankommt?
  Ihr wisst schon, wie man bei Laplace-Versuchen die Wahrscheinlichkeit berechnet: Anzahl der gewünschten Möglichkeiten durch Anzahl aller Möglichkeiten.
  Da eine Ampelphase 15s+30s=45s dauert, ist 45 die Anzahl aller Möglichkeiten.
  Die Anzahl der gewünschten Möglichkeiten (Anzahl der Sekunden mit Farbe Grün) ist 15.
  Also beträgt die Wahrscheinlichkeit für Grün an der 1. Ampel p(1. Ampel Grün)=15/45=1/3.
  Ebenso ergibt sich für Grün an der 2. Ampel p(2. Ampel Grün)=20/50=2/5 und für Grün an der 3. Ampel p(3. Ampel Grün)=30/80=3/8.
• Schreibt man in seinem Tagebuch auf, welche Ampel welche Farbe gezeigt hat, so gibt es die verschiedensten Möglichkeiten, z. B.
  1. Ampel Rot, 2. Ampel Grün, 3. Ampel Grün (kurz r,g,g) oder 
  1. Ampel Grün, 2. Ampel Rot, 3. Ampel Grün (kurz g,r,g).
  Wie viele verschiedene Möglichkeiten gibt es?
  Es ist sinnvoll, nach einem bestimmten Schema die Möglichkeiten aufzuschreiben, z. B. in einer Tabelle, in der der reihe nach die Fälle mit 0-mal Rot, 1-mal Rot, 2-mal Rot und 3-mal Rot aufgelistet werden:
  Man sieht: es gibt 8 verschiedene Möglichkeiten.
  Eine weitere sinnvolle Darstellung ist das Baumdiagramm.
  Man schreibt und liest das Baumdiagramm von links nach rechts: Erst kommt die Entscheidung zwischen Grün und Rot an der 1. Ampel, dann je nach Beobachtung die Entscheidung für die 2. Ampel usw.:
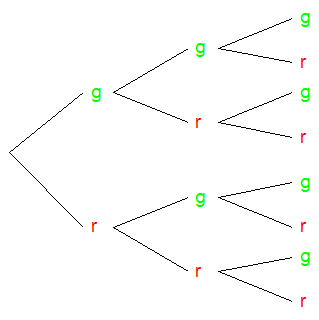  Auch hier sieht man, dass es 8 verschiedene Möglichkeiten für die Beobachtung gibt.

• Schreibt man jeweils die Wahrscheinlichkeiten an das Baumdiagramm, mit denen die jeweilige Farbe auftritt, so kann man die Wahrscheinlichkeit für eine bestimmte Aufeinanderfolge von 3 Ampelfarben berechnen:
             
  Die Zahlen in der rechten Abbildungen beziehen sich auf den Fall, dass man 120-mal die Ampeln beobachtet hat.
  Wenn die Beobachtungen genau so ausgefallen sein sollten, wie die berechneten Wahrscheinlichkeiten vorhersagen (was allerdings sehr unwahrscheinlich ist), so ergebn sich für die verschiedenen Fälle die großen Zahlen ganz rechts. 3-mal Grün würde dann also 6-mal bei 120 Beobachtungen auftreten. Daraus kann man die Wahrscheinlichkeit 1/20 für diesen Fall berechnen (siehe ganz rechts).
• Was haben nun die Wahrscheinlichkeiten in der linken Abbildung mit den Wahrscheinlichkeiten in der rechten Abbildung zu tun?
  Nehmen wir mal den Fall g,g,g:
  Die 40 ergibt sich aus der 120 durch 120·1/3=40.
  Aus der 40 entsteht die 16 durch 40·2/5=16.
  Und aus der 16 entsteht die 6 durch 16·3/8=6.
  Zusammengefasst ergibt sich also die 6 aus der 120 durch 120·1/3·2/5·3/8=6.
  Dividieren wir noch durch 120, so ergibt sich 1/3·2/5·3/8=6/120=1/20.
  Wenn man also die Wahrscheinlichkeiten links am Pfad entlang multipliziert, so ergibt sich die Wahrscheinlichkeit für das gesamte Ergebnis.

• Die Wahrscheinlichkeit für einen einzelnen Versuchsausgang erhält man, indem man die Wahrscheinlichkeiten entlang des Pfades multipliziert.
• Will man die Wahrscheinlichkeit für mehrere Pfade erhalten, so muss man die Wahrscheinlichkeiten für die betreffenden Pfade addieren.
• Beispiel:
  Gesucht ist die Wahrscheinlichkeit dafür, dass 2 Ampeln Rot zeigen und eine Ampel Grün (siehe 2009-02-24).
  Zunächst sucht man die Wahrscheinlichkeiten für die Pfade (g;g;r), (g;r;g), (r;g;g). Das sind 10/120, 9/120 und 12/120.
  Die Addition ergibt 10/120+9/120+12/120=31/120. Das Ergebnis ist die gesuchte Wahrscheinlichkeit.

• Pfadregeln
• Die Wahrscheinlichkeiten entlang eines Pfades (von links nach rechts) werden multipliziert.
• Umfasst ein Ereignis mehrere Ausgänge des Versuchs, werden die Wahrscheinlichkeiten dieser Ausgänge (von oben nach unten) addiert.

• Besprechung und Rückgabe der Klassenarbeit 3 ( Aufgaben | Lösungen )

• Übungsaufgabe zu Glücksrädern und Baumdiagrammen
  
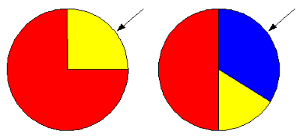
• Anmerkungen zu Euren Lösungen 
• Einige haben an die Pfade des Baumdiagramms Prozentzahlen für die Wahrscheinlichkeiten geschrieben, z. B. 75% für Rot bei der linken Scheibe und 50% für Rot bei der rechten Scheibe.
  Achtung: Wenn jetzt die Wahrscheinlichkeiten an den Pfaden für die Gesamtwahrscheinlichkeit multipliziert werden, ist 75%·50% nicht 3750%.
  Wegen 75%=75/100 und 50%=50/100 gilt 75%·50%=75/100·50/100=(75·50)/(100·100)=3750/10000=0,375=37,5%
• Günstiger ist es, die Wahrscheinlichkeiten als Bruch zu schreiben. Da gilt für Rot-Rot: 3/4·1/2=3/8.
• Bei der rechten Scheibe haben einige für den gelben Bereich die Wahrscheinlichkeit 1/6, andere 1/5 angegeben. Man kann entscheiden, welcher Werte eher zutrifft, wenn man den Winkel abmisst, den der gelbe Sektor im Mittelpunkt besitzt. Ist der Winkel 60°, so ist die Wahrscheinlichkeit 1/6, da 60° ein Sechstel von 360° ist.
  Für die Wahrscheinlichkeit 1/5 muss der gelbe Sektor den Winkel 72° aufweisen.

• Eine Heftzwecke fällt entweder auf die Seite  oder auf den Kopf .
  Ihr solltet in Gruppen herausfinden, mit welcher Wahrscheinlichkeit welcher Fall eintritt.
  Als Arbeitsmaterial habt Ihr 10 Heftzwecken pro Gruppe erhalten. 
  In der nächsten Stunde werden wir von Euch erfahren, welche Methode Ihr zum Ermitteln der Wahrscheinlichkeit eingesetzt habt und zu welchem Ergebnis Ihr gekommen seid.

• Zur Auswertung Eurer 7 Gruppenergebnisse aus der letzten Stunde haben wir die Werte im Listeneditor in den Taschenrechner eingegeben:
         
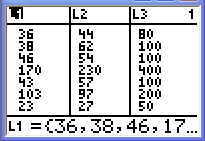
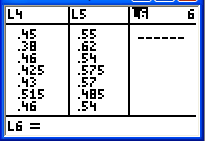
• In Liste L1 steht jeweils die Anzahl der Fälle, in denen in der Gruppe gewürfelt wurde.
• In Liste L2 steht jeweils die ANzahl der Fälle, in denen in der Gruppe gewürfelt wurde.
• Liste L3 enthält die Summe L1+L2. Dort steht also, wie viele Heftzwecken insgesamt gewürfelt wurden.
• Liste L4 enthält die Formel L1/L3. Es wird also die relative Häufigkeit berechnet dafür, dass die Heftzwecke mit der Spitze nach oben gefallen ist.
• Liste L5 enthält die Formel L2/L3. Es wird also die relative Häufigkeit berechnet dafür, dass die Heftzwecke mit der Spitze schräg nach unten gefallen ist.
• Wir sehen: Bei allen Gruppen bis auf Gruppe 6 ist die Heftzwecke immer so gefallen.
  Sollte man aus den relativen Häufigkeiten Werte für die Wahrscheinlichkeit ermitteln, würden diese Werte sehr unterschiedlich sein.
• Wir wenden deshalb das Gesetz der großen Zahlen an und fassen alle Versuche zu einem großen Ergebnis zusammen:
  In den Formeln wird mit sum(L4) und sum(L5) die Summe aller Zahlen in Liste 4 und in Liste 5 berechnet.
  dim(L4) und dim(L5) gibt an, wie viele Werte in den Listen stehen, wie viele Gruppen wir also berücksichtigt haben.
  Die Mittelwerte ergeben sich dann aus den Formeln sum(L4)/dim(L4) und sum(L5)/dim(L5).
• Gerundet ergeben sich also folgende Wahrscheinlichkeiten:
  p()=0,45=45%   ;    p()=0,55=55%.

• Die Auswertung der Hausaufgabe ergab, dass die zu Hause ermittelten Wahrscheinlichkeiten nicht unbedingt mit den in der Schule gefundenen Wahrscheinlichkeiten übereinstimmten.
  Als Gründe haben wir festgehalten:
• Bei Zufallsversuchen kann man nie das Ergebnis exakt voraussagen.
• Wenn man zu Hause mit anderen Heftzwecken als in der Schule würfelt, können sich natürlich auch andere Ergebnisse ergeben.
• Weitere Übung zum Erstellen von Baumdiagrammen.

• Übungsaufgabe mit zwei Teilaufgaben, in denen ein 2-stufiger Zufallsversuch mit gleichen Wahrscheinlichkeiten beschrieben wird:
  1. Blutspender unter und über 20 Jahre alt - Blutgruppe 0 und andere.
  2. Ergebnisse in einer Deutsch-Klassenarbeit - Ergebnisse in einer Englisch-Klassenarbeit.
  Warum sind diese beiden Zufallsversuche nicht gleich zu behandeln? Die Lösung werden wir hoffentlich in der nächsten Stunde finden.

• Lösung zur letzten Stunde:
  Die beiden Aufgaben sind nicht gleich zu bearbeiten, weil bei der 2. Aufgabe die Wahrscheinlichkeiten für "gute Deutscharbeit" und "gute Englischarbeit" nicht unabhängig voneinander sind.
  Beim Baumdiagramm müssten also nach der 1. Verzweigung für "gute Deutscharbeit" je nach Ausgang andere (aber hier unbekannte) Wahrscheinlichkeiten für die "gute Englischarbeit" eingesetzt werden.
  Man spricht bei solchen voneinander abhängigen Wahrscheinlichkeiten von "bedingter Wahrscheinlichkeit". Damit werden wir uns aber später intensiver beschäftigen.
• Ihr habt in Gruppen Zufallsversuche durchgeführt mit a) 3 roten und 4 gelben Kugeln, b) 3 roten und 3 gelben Kugeln und c) mit 6 roten und 3 gelben Kugeln.
  Ihr solltet 2-mal ohne Zurücklegen eine Kugel ziehen und prüfen, ob Ihr 2 Kugeln derselben Farbe gezogen habt.
  Dieses Ereignis trat bei Euch am häufigsten bei c) auf, weniger bei b) und am wenigsten bei a).
  Hausaufgabe: Wenn Ihr Euch theoretisch (rechnerisch) überlegt, bei welchem Fall am häufigsten 2 gleichfarbige Kugeln auftreten, erhaltet Ihr dann dasselbe Ergebnis?

• Besprechung der Hausaufgabe

• reduzierte Baumdiagramme
  Benötigt man nicht alle Zweige eines Baumdiagramms, so kann man sich auf die benötigten Zweige beschränken.
  Häufig ist es nur so möglich, umfangreichere Baumdiagramme im Heft zu zeichnen.
  Beispiel: Die Wahrscheinlichkeiten, ein rotes, ein gelbes oder ein blaues Feld bei einem Glücksrad zu treffen, betragen 1/6, 3/6 und 2/6
  Es ist nach der Wahrscheinlichkeit gefragt, dass beim 3-maligen Drehen keine Farbe doppelt oder dreifach vorkommt.
   
  Statt des linken kann besser das rechte Baumdiagramm benutzt werden. Dort sind nur die Pfade verzeichnet, die zur Berechnung der Wahrscheinlichkeit benötigt werden.

• Besprechung der Hausaufgabe
• Weitere Übungen zu reduzierten Baumdiagrammen.

• Auch heute wieder Übungen zu reduzierten Baumdiagrammen.

• Übungen zu reduzierten Baumdiagrammen und zum Berechnen von Wahrscheinlichkeiten durch die Wahrscheinlichkeit des Gegenereignisses.

• Übungen zur Arbeit.

• Klassenarbeit 4

• Rückgabe der Klassenarbeit 4  [ Aufgaben , Lösungen ]