Bestimmung von π mit der Monte-Carlo-Methode
Zur Bestimmung von krummlinig begrenzten Flächen nutzt man üblicherweise die
Integralrechnung.
Es gibt aber zahlreiche andere Verfahren, die auf Grund von
Näherungsverfahren (fast) beliebig genaue Näherungswerte des Flächeninhalts
liefern können.
Eines davon ist die Monte-Carlo-Methode.
Mit Zufallszahlen, die auf unterschiedlichste Art erzeugt werden können,
werden Flächeninhalts-Verhältnisse gegeneinander abgeschätzt.
Kennt man einen Flächeninhalt, kann der unbekannte Flächeninhalt dann
näherungsweise bestimmt werden.
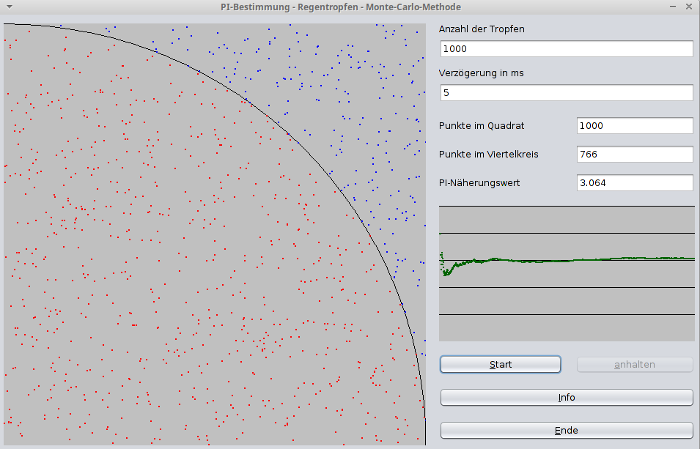
Ein Beispiel für dieses Vorgehen ist das "Regentropfenverfahren" zur
Bestimmung des π-Wertes.
In ein Quadrat mit der Seitenlänge r zeichnet man einen Viertelkreis mit dem
Radius r ein.
Nun lässt man per Zufallszahlengenerator zufällige Koordinaten von Punkten
in diesem Quadrat berechnen und trägt diese Punkte in die Zeichnung ein.
Man zählt, wieviele dieser Punkte in dem Viertelkreis liegen (PViertelkreis)
und teilt diese Zahl durch die Anzahl aller Punkte (Palle).
Der Quotient ist ein Maß für das Verhältnis des Flächeninhaltes des
Viertelkreises (1/4·π·r²) zum Flächeninhalt des Quadrates (r²).

JavaScript-Proramm
Java-Programm zum Regentropfenverfahren zur
Offline-Nutzung: