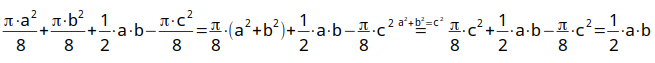Möndchen des Hippokrates
Im Rahmen von Kreisflächenberechnungen taucht immer wieder die Zahl π
auf (Kreisflächeninhalt: π·r² ; Kreisumfang: 2·π·r).
Überraschend sind entsprechend die Fälle, in denen Flächen, die von
Kreisbögen begrenzt werden, rational (=durch Brüche mit ganzen Zahlen im
Zähler und Nenner, also ohne die transzendente Zahl π) darstellbare
Flächeninhalte besitzen.
Ein Beispiel dafür sind die "Möndchen
des
Hippokrates".
Der Flächeninhalt der gelben Möndchen ist insgesamt genau so groß wie der
Flächeninhalt des roten Dreiecks.
Im Java-Programm kann der Punkt auf
dem großen Kreisbogen mit dem Schieberegler gezogen werden.

Beweis der Flächengleichheit:
Zunächst werden die Flächen der Halbkreise über den Seiten a und b und die
Fläche des rechtwinkligen Dreiecks berechnet:
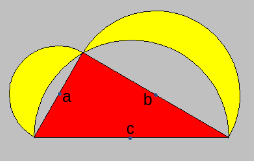

Subtrahiert man von der Summe dieser Flächeninhalte den Flächeninhalt des
Halbkreises über der Seite c, so erhält man die Flächeninhalte der beiden
gelben Halbmonde:
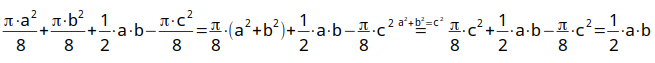
und das ist gleichzeitig der Flächeninahlt des roten Dreiecks.