Bestimmung von π mit dem Nadelproblem von Buffon
Georges-Louis Leclerc de Buffon (1707-1788) hat im Zusammenhang mit
Berechnungen zu Glücksspielen u. a. folgendes Problem untersucht:
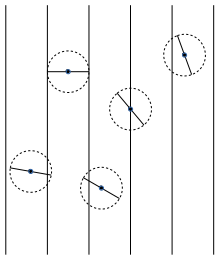
Auf einen Untergrund, auf den in gleichem Abstand parallele Geraden
gezeichnet sind, werden Nadeln fallen gelassen.
Die Nadeln sind so lang wie die Breite der Streifen.
Überlagert eine Nadel eine der Geraden oder berührt sie, so gilt das als
Erfolg.
De Buffon zeigte, dass die Wahrscheinlichkeit für einen Erfolg 2/π≈ 0,6366
beträgt.
In der Skizze hatte man mit den 4 linken Nadeln Erfolg, die rechte Nadel
bedeutet Misserfolg.
Im der Simulation wird links das Fallen der Nadeln simuliert. Grüne
Nadeln treffen eine Gerade und bedeuten Erfolg, die roten Nadeln treffen
die Geraden nicht und stehen für Misserfolg.
Die Anzahl der Nadeln und die Verzögerung zwischen dem Fallen zweier
Nadeln sind frei wählbar.
Im rechten BIld werden die Versuchsergebnisse grafisch dargestellt.
Nach Beendigung eines Versuchs oder nach "Anhalten" kann mit "Start" ein
nächster Versuch gestartet werden, dessen Ergebnisse zu denen der
vorherigen Versuche addiert wird.
Das folgende Java-Programm ist zum Herunterladen für die
Offline-Benutzung geeignet.
Im Programm wird links das Fallen der Nadeln
simuliert. Rote Nadeln treffen eine Gerade und bedeuten Erfolg, die blauen
Nadeln stehen für Misserfolg.
Rechts oben können die Anzahl der fallenden Nadeln und die Wartezeit
zwischen zwei fallenden Nadeln in ms eingegeben werden.
Darunter werden die Anzahl der schon gefallenen Nadeln und die Treffer
registriert.
Der Näherungswert für π wird nach der Formel π ≈ 2 · alle gefallenen Nadel /
alle schneidenden Nadeln berechnet.

Beweis des Buffonschen Ergebnisses:
Voraussetzung ist lediglich, dass die Geraden parallel verlaufen und alle
Geraden denselben Abstand von den beiden benachbarten Geraden haben.
Außerdem soll die Nadellänge gleich dem Abstand der Geraden sein.
Zunächst einige Vereinfachungen:
Die Nadeln werden per Zufall gesetzt, indem zunächst ein Punkt in der Ebene
ausgewürfelt wird und dann ein Winkel zufällig bestimmt wird, unter dem die
Nadel zu liegen kommt.
Für die Frage nach Erfolg oder Misserfolg spielt der y-Wert des Punktes
keine Rolle. Wir beschränken uns also auf die x-Achse.
Der Abstand und die Nadellänge müssen gleich sein. Auf den Wert kommt es
dabei nicht an. Wir wählen deshalb für den Abstand und die Nadellänge den
Wert 1.
Es reicht, einen Streifen zu untersuchen, da nicht die genaue Lage auf der
x-Achse, sondern nur die Lage des Mittelpunktes der Nadel innerhalb eines
Streifens wichtig ist. Die linke Gerade wählen wir so, dass sie auf der
y-Achse liegt.

Für 0<x<1/2 gibt es Nadeln, die die linke Gerade schneiden. Für einen
Mittelpunkt der Nadel im Anstand x von der y-Achse sind die entsprechenden
Endpunkte der Nadel in der Skizze rot gefärbt. Dazu gehört der Winkelbereich
α. Das eingezeichnete rechtwinklige Dreieck hat die Hypotenuse 1/2, die der
halben Nadellänge entspricht.
Die Länge des roten Kreisbogens hat für x=0 den Wert π (Halbkreis) und für
x=1/2 den Wert 0.
Die Wahrscheinlichkeit p(x), dass für ein x die Gerade geschnitten wird, ist
also der Quotient aus der Bogenlänge b(x) und der Halbkreis-Länge π.
Für die Berechnung der Wahrscheinlichkeit für beliebiges x (Summe s1)
muss dann über alle Wahrscheinlichkeiten summiert werden (Integration wegen
kontinuierlicher x-Werte) und das Ergebnis muss noch verdoppelt werden für
den symmetrischen Teil von 1/2<x<1 (Summe s2).

Soll das auf dem Buffonschen Nadelproblem beruhende Glücksspiel fair sein
(50% Gewinn, 50% Misserfolg), muss die Wahrscheinlichkeit für einen Gewinn
gesenkt werden. Das geschieht durch eine kürzere Nadellänge auf den Wert N.
Die Summe s1+s2 muss dann den Wert 0,5 haben:

Das zugehörige Programm simuliert das faire
Spiel:

Wer experimentieren möchte, findet hier das Programm
mit Eingabemöglichkeit für unterschiedliche Nadellängen.
Screenshot für Nadellänge = 0,4 ∙ Abstand der Geraden







