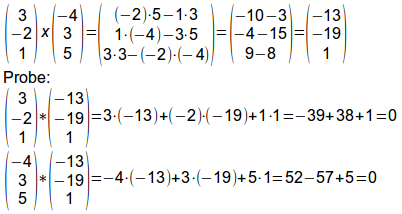Unterrichtseinsichten - Schuljahr 2015/2016 - Mathematik 12ma5g
Vektorrechnung
2015-09-03
- Punkte im Koordinatensystem
In der nächsten Zeit werden wir mit dreidimensionalen Koodinatensystemen
arbeiten.
Da die 3 Koordinatenachsen paarweise zueinander senkrecht stehen, kann
man Punkte in zweidimensionaler Darstellung nicht exakt identifizieren.
Üblicherweise wird die y-Achse waagrecht abgetragen, die z-Achse
senkrecht und die x-Achse im Winkel von 45° zu den beiden anderen
Achsen, wobei die positiven Werte nach links unten abgetragen werden.
Die Abstände zwischen 2 Gitterpunkten werden dabei als 2 Einheiten
gezählt:

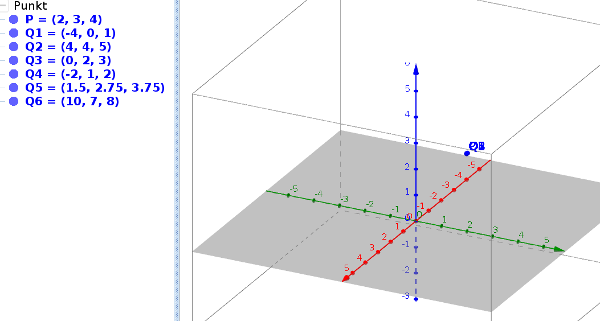
Der Punkt P ist durch seine Koordinaten (2/3/4) gegeben.
Die roten, grünen und blauen Streckenzüge zeigen, dass man in beliebiger
Reihenfolge die Koordinaten abtragen kann und man dennoch an derselben
Stelle P landet.
Ergänzt man die entstehende Figur durch die 3 gelben Strecken, ergibt
sich ein Quader. Der Koordinatenursprung und der Punkt P sind dabei
Endpunkte einer Diagonale des Quaders.
Es gibt weitere Punkte Qi, die an derselben Stelle wie der
Punkt P im Koordinatensystem eingetrragen werden müssen. Die Darstellung
ist also nicht eindeutig.
Folgende Punkte wurden von den Kursteilnehmern gefunden: Q1(-4/0/1);
Q2(4/4/5); Q3(0/2/3); Q4(-2/1/2); Q5(1,5/2,75/3,75);
Q6(10/7/8)
Darstellung der Punkte mit GeoGebra:
 download
der GeoGebra-Datei
download
der GeoGebra-Datei
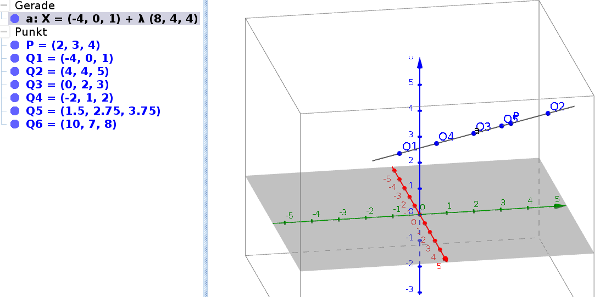
Schaut man sich das Koordinatensystem aus einem anderen Blickwinkel an,
erkennt man, dass alle Punkte auf einer Geraden liegen und die
verschiedenartige Darstellung daher kommt, dass man in Richtung der
Geraden sieht.
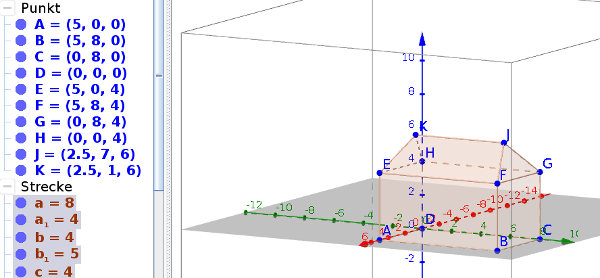
- Aufgabe: Zeichne ein Haus, der Länge 8m, der Breite 5m und der Höhe
4m, auf das ein abgeschrägtes symmetrisches Dach gesetzt ist, dessen
First 6m lang ist.
 download der GeoGebra-Datei
download der GeoGebra-Datei
- Spiegelung an einer Koordinatenebene
Ein Objekt wird an einer Koordinatenebene gespiegelt, indem die nicht
beteiligte Koordinate invertiert wird (= mit -1 multipliziert).
Spiegelung an x-y-Ebene: Die z-Koordinate wird mit -1 multipliziert.
Spiegelung an x-z-Ebene: Die y-Koordinate wird mit -1 multipliziert.
Spiegelung an y-z-Ebene: Die x-Koordinate wird mit -1 multipliziert.
Beispiel: Spiegelung an der x-y-Ebene:
 download
der GeoGebra-Datei
download
der GeoGebra-Datei
2015-09-08
- Wie bestimmt man Abstände zwischen Punkten?
- Auf einem Zahlenstrahl berechnet man die Differenz der beiden Werte
der Punkte:

Ein Pfeil zeigt von A nach B. Seine Länge ist der Abstand: 5-2=3
- In der Ebene hat der Pfeil Komponenten in x- und in y-Richtung:
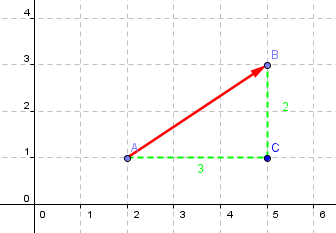
Man misst die Ausdehnung in x-Richtung und in y-Richtung:
x-Richtung: 5-2=3
y-Richtung: 3-1=2
Mit Hilfe des Satzes des Pythagoras kann man nun die Länge des Pfeils,
also den Abstand der Punkte, berechnen:

- Im 3-dim-Raum besitzt der Pfeil S1 von P1(2/1/4) nach P2(5/3/9)
Komponenten in x-, y- und z-Richtung:

Man misst die Ausdehnung in x-Richtung und in y-Richtung:
x-Richtung: 5-2=3
y-Richtung: 3-1=2
z-Richtung: 9-4=5
Mit Hilfe des (erweiterten) Satzes des Pythagoras kann man nun die
Länge des Pfeils, also den Abstand der Punkte, berechnen:

- Die oben betrachteten Pfeile sind durch ihre Ausdehnung in x-, y- und
z-Richtung festgelegt.
Sie würden gleiche Länge und gleiche Richtung haben, wenn man alle
Punkte um konstante Werte in x-, y- oder z-Richtung verschieben würde.
Als Repräsentanten für alle Pfeile, die in gleiche Richtung verlaufen
und gleiche Länge haben definiert man einen Vektor, der durch die oben
gefundenen Ausdehnungen in x-, y- und z-Richtung dargestellt wird.
Vektoren werden durch kleine Buchstaben gekennzeichnet, die zur
Unterscheidung von Geraden oder Strecken durch einen darübergesetzten
Pfeil ausgezeichnet werden.
Die Zahlenwerte, die die Ausdehnungen der Pfeile in x-, y- und
z-Richtung beschreiben, werden in große runde Klammern gesetzt.
Für den 1-dimensionalen Fall benutzt man normalerweise keine Vektoren.
2-dimensionaler Fall (Ebene): 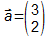
3-dimensionaler Fall (Raum): 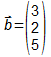
- Bei den Vektoren werden die Ausdehnungen in Richtung der
Koordinatenachsen vom Anfang des Pfeils zur Spitze des Pfeils gemessen.
2 Vektoren sind gleich, wenn sie in dieselbe Richtung zeigen und gleiche
Länge haben.
Einen Vektor mit gleicher Länge aber genau entgegengesetzter Richtung
nennt man Gegenvektor und beschreibt ihn durch ein Minuszeichen vor dem
Buchstaben bzw. vor den Komponenten.
Vektoren, die in der Länge oder der Richtung oder in beiden
Eigenschaften nicht übereinstimmen, sind ungleich.
- Beispiele (hier ohne Pfeil geschrieben):
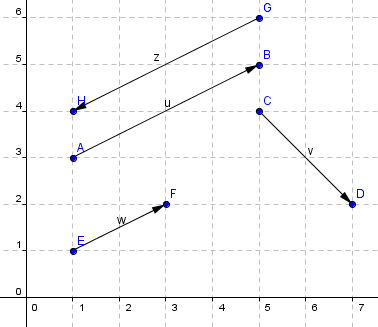
u und z sind Gegenvektoren
u und w sind nicht gleich, da sie unterschiedliche Länge haben
w und v sind nicht gleich, da sie unterschiedliche Länge und Richtung
haben
- Definition von Ortsvektor und Richtungsvektor
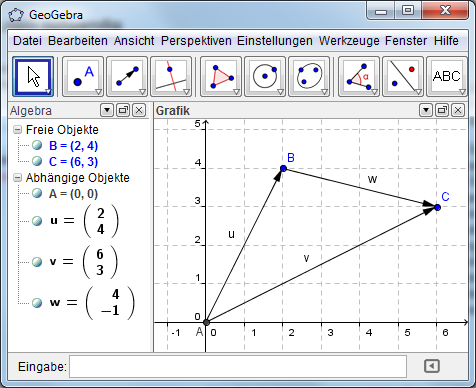
Ortsvektoren kennzeichnen beliebige Punkte im Koordinatensystem, indem
der Beginn des zum Ortsvektors gehörenden Pfeils im Koordinatenursprung
liegt und die Spitze am zu bezeichnenden Punkt.
Die Komponenten des Ortsvektors stimmen mit den Koordinaten des zu
bezeichnenden Punkts überein (siehe u und v).
Richtungsvektoren geben eine Richtung an. Z. B. wird die Richtung vom
Punkt B zum Punkt C durch den Richtungsvektor w angegeben. Der Vektor
kann so lang sein wie der Abstand der beiden Punkte, muss es aber nicht.
Nur die Richtung ist festgelegt.
- Angenommen, die Komponenten von v wären nicht bekannt. Dann könnte man
mit Hilfe der Vektoren u und w diese Komponenten berechnen:
Die Ausdehnung des Vektors v in x-Richtung ist so groß wie die Summe der
Ausrichtungen der Vektoren u und w in x-Richtung.
Für die y-Richtung gilt das analog.
Man schreibt deshalb als Summe: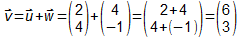
- Vektoren werden addiert, indem man die Komponenten der Vektoren
addiert.
2015-09-11
- Vektoren werden subtrahiert, indem man die Komponenten der Vektoren
subtrahiert.
- In Verallgemeinerung zum Beispiel aus der letzten Stunde gilt:
Der Vektor von einem Punkt zu einem anderne Punkt ergibt sich, indem man
vom ersten Punkt beginnend auf Wegen geht, die durch Vektoren vorgegeben
sind, bis man beim Zielpunkt landet. Die benutzten Vektoren addiert man.
Beispiel:
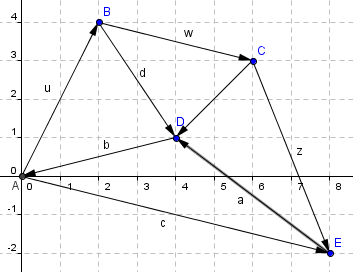
Der Vektor c lässt sich darstellen durch:

- Alles oben Gesagte gilt auch für den 3-dimensionalen Fall.
- Vielfache eines Vektors:
-
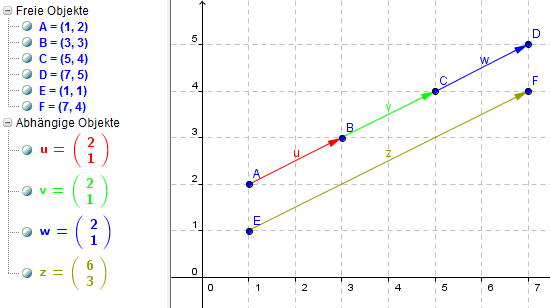
Einen Vektor multipliziert man mit einer Zahl (= einem Skalar), indem
man jede Komponente des Vektors mit dieser Zahl multipliziert:

Allgemein: 
2015-09-15
- Hilfe zur Hausaufgabe:
Gegeben sind die Punkte A(2/4/-3), B(0/6/-2) und C(t/4/-4)
Frage: Sind die 3 Punkte Ecken eines gleichseitigen oder wenigstens
gleichschenkligen Dreiecks?
Lösung: Zu untersuchen ist, ob die Dreiecksseiten gleich lang sind.
Die Länge einer Seite bestimmt man, indem man zunächst den Vektor
bestimmt, der von einem Eckpunkt zum anderen geht und dann die Länge des
Vektors berechnet.
Da A und B vollständig bestimmt sind, wird zunächst der Abstand AB
berechnet.
Dann untersucht man, ob man den Wert für t so wählen kann, dass AC=AB
und/oder BC=AB.
Die Ortsvektoren zu A, B und C werden durch entsprechende kleine
Buchstaben a, b und c bezeichnet.

Da von den 4 Lösungen für t keine 2 übereinstimmen, gibt es 4
Möglichkeiten für ein gleichschenkliges Dreieck aber keine Möglichkeit
für ein gleichseitiges Dreieck.
- Geradengleichung:

Eine Gerade und damit alle Punkte auf einer Geraden kann man so
bestimmen, indem man zunächst mit einem Ortsvektor vom 0-Punkt zu einem
Punkt der Geraden geht und dann auf der Geraden entlang mit dem
Vielfachen eines Richtungsvektors bis zu dem zu beschreibenden Punkt
läuft.
Im Beispiel wird der Punkt C durch die Vektoren u und v beschrieben: 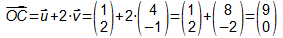
Allgemeine Gleichung einer Geraden: 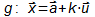
- Punktprobe
Will man wissen, ob der Punkt P(15/-3) auf der oben beschriebenen
Geraden liegt, so setzt man den Ortsvektor für P als Vektor x ein und
untersucht, ob es einen einzigen k-Wert gibt:

Da die k-Werte nicht übereinstimmen, liegt der Punkt P nicht auf der
Geraden.
2015-09-17
- Übungen zu Geradengleichungen
- Durch die Punkte A(5/2/-4) und B(-1/3/2) soll die Gerade g
verlaufen. O(0/0/0) sei der Koordinatenursprung.

- Aufgabe: Stelle unterschiedliche Geradengleichungen auf.
Lösung: Mit einem beliebigen Ortsvektor gelangt man zur Geraden und
dann mit einem beliebig langen Richtungsvektor zu einem Punkt der
Gerade.
Ortsvektoren sind zum Beispiel a und b, aber auch jeder andere Vektor
zur Geraden.
Richtungsvektor ist v, aber auch jeder Vektor, der dieselbe Richtung
wie v haben muss aber auch andere Längen haben darf.
Beispiele: Alle angegebenen Geradengleichungen beschreiben dieselbe
Gerade. Der t-Wert ist für einen bestimmten Punkt jeweils
unterschiedlich.

- Der Punkt C(2/y/z) soll auf der Geraden liegen. Bestimme y und z.

- Gibt es einen Punkt P(p, p, p), dessen Koordinaten alle den gleichen
Wert haben?

- Zu berechnen sind die Koordinaten des Punktes S, in dem die Gerade
die y-z-Ebene schneidet.
Da in der y-z-Ebene alle Punkte die x-Koordinate 0 besitzen, hat der
gesuchte Punkt S die Koordinaten S(0, y, z)

2015-09-22
- Weitere Übung zu Geradengleichungen:
- Es sind viele Punkte gegeben durch die Angabe ihrer Koordinaten in
Verbindung mit einem Parameter: P(2+3t/6t/-4-2t)
Setzt man für t einen Wert ein, so erhält man die Koordinaten eines
Punktes dieser Punkteschar.
Beispiele:
t=1: P1(2+3/6/-4-2)=P1(5/6/-6)
t=-2: P-2(2-6/-12/-4+4)=P-2(-4/-12/0)
- Bildet man den Ortsvektor zu einem allgemeinen Punkt der
Punkteschar, so lässt sich dieser Vektor umformen, bis sich eine
Geradengleichung ergibt.
Alle Punkte der Punkteschar bilden also eine Gerade.

Bildet man aus den beiden Punkten für t=1 und t=-2 eine
Geradengleichung, so ergibt sich:

- Wird durch die beiden Gleichungen, die so verschieden aussehen,
wirklich eine einzige Gerade beschrieben?
Wir sehen, dass der obere Richtungsvektor mit -3 multipliziert den
unteren Richtungsvektor ergibt. Die Richtungsvektoren zeigen also die
gleiche Richtung an und damit sind die beiden Geraden bestimmt schon
einmal parallel.
- Zeigen denn die beiden Ortsvektoren zur selben Gerade?
Dazu machen wir die Punktprobe und setzen die Ortsvektoren jeweils in
die andere Geradengleichung ein:

Jedesmal ergibt sich ein identischer Wert für den Parameter. Die
Gleichungen beschreiben also die gleiche Gerade.
- Statt der Punktprobe mit 2 Punkten kann man sich auch einfacher
überlegen:
Wenn die beiden Geradengleichungen dieselbe Gerade beschreiben, dann
muss die Verbindungslinie der zu den Ortsvektoren gehörenden Punkte
parallel zu den Richtungsvektoren sein (man geht von einem Punkt in
Richtung des Richtungsvektors zu dem anderen Punkt). Dasselbe gilt
auch für die Ortsvektoren der beiden Beispielpunkte.
Verbindungsvektoren sind hier

- Merksatz:
2 Geraden sind parallel, wenn ihre Richtungsvektoren linear abhängig
sind (d. h. sie zeigen in die selbe Richtung, ein Richtungsvektor ist
ein Vielfaches des anderen Richtungsvektors).

2 parallele Geraden sind identisch, wenn die Differenz der Ortsvektoren
linear abhängig zu den Richtungsvektoren ist.
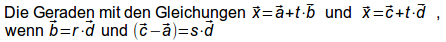
- Spiegelung an Korrdinatenebenen
Eine Gerade wird an einer Koordinatenebene gespiegelt, indem man in der
Geradengleichung die Komponenten der zur Ebene senkrecht stehenden Achse
mit -1 multipliziert.
Beispiele:
Spiegelung an der x-y-Ebene: Die z-Komponenten werden mit -1
multipliziert.
Spiegelung an der x-z-Ebene: Die y-Komponenten werden mit -1
multipliziert.
Spiegelung an der y-z-Ebene: Die x-Komponenten werden mit -1
multipliziert.
2015-09-24
- Besprechung der Hausaufgabe und Übersicht zum Thema "Geraden".
- Bei einer Geraden kann man nur in eine Richtung gehen. Es reicht also,
zum Stützvektor das Vielfache eines Richtungsvektors zu addieren, um zu
jedem Punkt der Geraden gelangen zu können.

- In einer Ebene sind aber 2 verschiedene Richtungen möglich (deshalb in
einem kartesischen Koordinatensystem auch die 2 Angaben bei einem Punkt
(x- und y-Koordinate)).
Man muss also, um jeden Punkt der Ebene erreichen zu können, zum
Stützvektor Vielfache von 2 Richtungsvektoren addieren:

 (download der
GeoGebra-Datei)
(download der
GeoGebra-Datei)
2015-09-29
- Schnitt von Gerade und Ebene

Die Gerade g durch E und C soll die durch das Rechteck DBFH gegebene
Ebene E schneiden.
Der Koordinatenursprung liege im Punkt A.
Lösung:

Während bei diesem Beispiel die Lösung des Gleichungssystems "per Hand"
noch gut durchzuführen ist, wird es im allgemeinen Fall mit sehr viel
Rechenaufwand verbunden sein. Alternativ kann man dann den
Taschenrechner benutzen und mit Hilfe des rref-Befehls für Matrizen die
Lösung sehr einfach bestimmen:

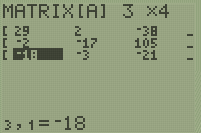




2015-10-01
- Wiederholung zur Klausur 1
2015-10-06
2015-10-08
- Vor der Klausur wurde besprochen, dass zwei Vektoren parallel sind,
wenn der eine ein Vielfaches des anderen Vektors ist.
- Wie kann man überprüfen, ob 2 Vektoren senkrecht zueinander stehen?
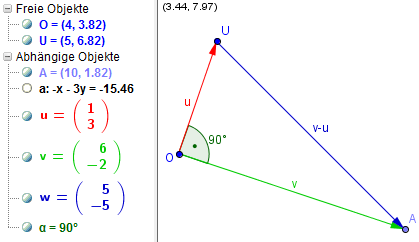
Das Bild zeigt den 2-dimensionalen Fall.
Rechnerisch untersucht wird das Problem am 3-dimensionalen Fall:
- Das von den Vektoren u, v und v-u gebildete Dreieck ist rechtwinklig.
Damit kann der Pythagoras auf die Dreiecksseiten angewendet werden:

Die Rechnung zeigt, dass die Summe der Produkte der einzelnen
Komponenten der Vektoren 0 ergibt, wenn die Vektoren senkrecht
zueinander stehen.
(Zu zeigen wäre eigentlich noch, dass die Vektoren nicht senkrecht
stehen, wenn die Summe nicht 0 ergibt)
- Wegen der Wichtigkeit dieser Beziehung hat die Summe den Namen
Skalarprodukt erhalten und man schreibt:
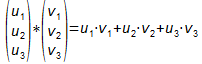
- Beispiel für den 2-dimensionalen Fall (siehe oben):

Gegenbeispiel (siehe oben):
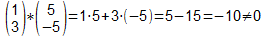
- Sind 2 Vektoren parallel zueinander, so ergibt das Skalarprdukt das
Produkt der Längen der Vektoren.
Beweis:
- Anwendungsbeispiele:
Gegeben sind die 3 grünen Vektoren a, b und c.

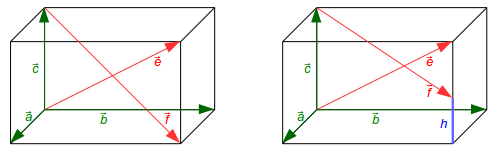
- Aufgabe 1:
Zu zeigen ist, dass die beiden Diagonalen e und f in der linken Figur
keinen Winkel von 90°
einschließen.
Zunächst: Die beiden Diagonalen schneiden sich, weil die Anfangspunkte
der Pfeile auf einer Geraden liegen und die Spitzen der Pfeile auf
einer dazu parallelen Gerade liegen. Deshalb liegen die beiden Pfeile
in einer Ebene.
Die roten Vektoren e und f werden gebildet. Dann wird mit dem
Skalarprodukt untersucht, ob die Vektoren senkrecht zueinander stehen.
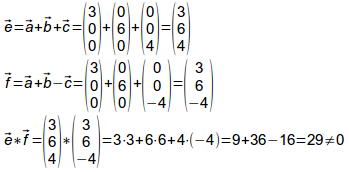
Da das Skalarprodukt nicht gleich 0 ist, schneiden sich die beiden
Vektoren e und f nicht
unter einem Winkel von 90°.
- Aufgabe 2:
Im rechten Bild trifft der Pfeil f in der Höhe h auf die Kante des
Quaders.
Zu berechnen ist der Wert von h für den Fall, dass sich die beiden
Pfeile unter dem Winkel 90° schneiden.
Rechnung wie oben, nur dass zum Schluss der Wert für h so bestimmt
wird, dass das Skalarprodukt den Wert 0 annimmt.

Das Skalarprodukt wird 0, wenn der Wert für h -11,25 beträgt, wenn
also die Pfeilspitze weit unterhalb des Quaders die senkrechte Kante
erreicht.
2015-10-13
- Rückgabe der Klausur 1 [ Aufgaben
| Lösungen
]
- Sind 2 Vektoren parallel zueinander, so ergibt das Skalarprdukt das
Produkt der Längen der Vektoren.
Beweis:
- Wir haben jetzt gesehen, dass das Skalarprodukt zweier senkrechter
Vektoren 0 ergibt und dass das Skalarprodukt zweier paralleler Vektoren
genau so groß ist wie das Produkt der Längen der beiden Vektoren.
Was ist nun aber, wenn die Vektoren unter einem beliebigen Winkel
zueinander stehen?
- Skizze:
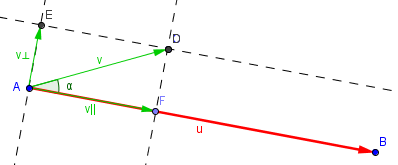
Die Vektoren u und v schließen den Winkel α ein.
v wird in zwei Komponenten v|| parallel zu u und v┴ senkrecht zu u
zerlegt.
Dann gilt:
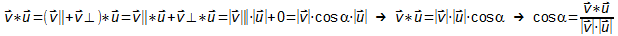
- Beispiel:
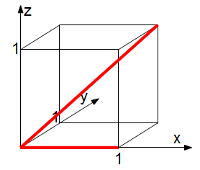
Berechne den Winkel, den die beiden roten Strecken einschließen.
Die Strecken können durch folgende Vektoren beschrieben werden: 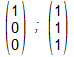
Dann folgt:
- Hausaufgabe:
Gegeben ist ein Würfel der Seitenlänge 1.
Zu berechnen ist der Winkel zwischen dem roten und dem grünen Vektor.

2015-10-15
- Besprechung der mündlichen Note
- Neben dem Skalarprodukt (mit einer Zahl als Ergebnis) gibt es noch das
Vektorprodukt (mit einem Vektor als Ergebnis), das nur im 3-dim-Raum
definiert ist.
Es dient z. B. in der Physik dazu, bei einem Elektronenstrahl in einem
Magnetfeld die Kraft auf die Elektronen zu bestimmen  .
.
Definition: Bei der Vektormultiplikation zweier 3-dim-Vektoren ergibt
sich ein Vektor, der senkrecht zu jedem der beiden Vektoren steht.
Gebildet wird dieser Vektor nach folgender Regel:

Beispiel:
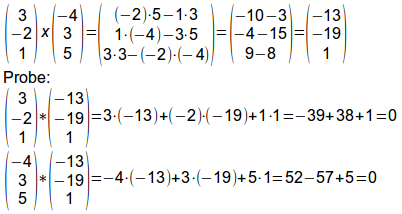
weiter mit Matrizen

 download
der GeoGebra-Datei
download
der GeoGebra-Datei
 download der GeoGebra-Datei
download der GeoGebra-Datei  download
der GeoGebra-Datei
download
der GeoGebra-Datei




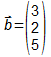


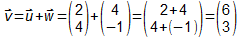







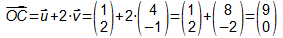
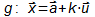











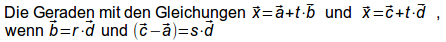








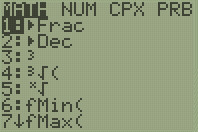




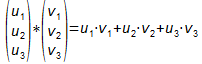

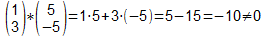



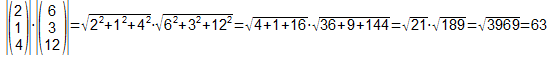


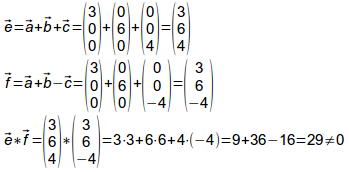


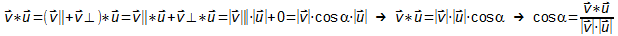

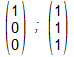


 .
.