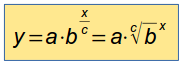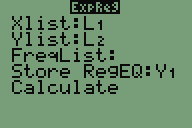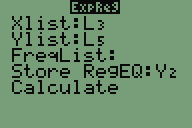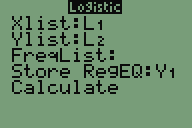Unterrichtseinsichten - Schuljahr 2015/2016 - Mathematik 12ma5g
Analysis II
2015-12-10
- Rückgabe der Abi-Probe-Klausur [ Aufgaben
| Lösungen
]
- Wiederholung zum Thema Logarithmen.
Hier ein Beitrag zum Rechnen
mit dem Rechenstab.
- Beweismethode "Vollständige Induktion" am Beispiel einer Rechenregel
für Logarithmen.

2015-12-15
- Wiederholung zu Exponentialfunktionen und zu exponentiellem Wachstum.
- Exponentialfunktionen der Form y=a∙bx:
Ist b>1, so liegt ein exponentielles Wachstum vor.
Ist b<1, so liegt eine exponentielle Abnahme vor.
- Beispiel:
Eine Bakterienkultur vergrößert sich in 5 Tagen um das 2,7-fache. Zu
Beginn sind 130 Bakterien vorhanden. Wieviel Bakterien sind es nach 17
Tagen?
Die Gleichung y=130∙2,7x ist falsch, da dann schon nach 1
Tag das 2,7-fache vorhanden wäre.
Man muss den Exponenten so ändern, dass jeweils nach 5 Tagen der
Exponent um 1 zunimmt.
Das geschieht durch Division von x durch 5: y=130∙2,7x/5,
denn wenn x=5, dann ist 5/5=1, bei x=10 ist 10/5=2 usw.
- Ergebnis

- Lösung der Aufgabe:
x=17 → y=130∙2,717/5=3807
- Man kann die Gleichung auch so umformen, dass im Exponenten nur x
steht:
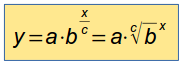
Die Basis gibt jetzt den Wachstumsfaktor für 1 Zeitschritt bzw. 1
Wegschritt an.
- Berechnung der Funktionsgleichung einer Exponentialfunktion bei
Kenntnis zweier Punkte eines Graphen
- Einsetzverfahren:

- Divisionsverfahren:

2016-01-12
- Begrenztes Wachstum
- Einführende Aufgabe:
Der Kaffee in einer Tasse hat die Temperatur ϑ=90°C. Die
Zimmertemperatur beträgt 20°C. In 1 Minute nimmt die Temperatur des
Kaffees um 20% bezogen auf den Unterschied zur Raumtemperatur ab.
Zu berechnen ist, wann die Temperatur 40°C beträgt.
Lösung: Die bisher benutzte Wachstums- und Zerfallsgleichung ϑ=a·ek·t
kann hier nicht benutzt werden, da dann für sehr große t-Werte die
Temperatur gegen 0°C gehen würde. Addiert man zum rechten Term aber noch
die Zimmertemperatur, so geht für große t die Temperatur gegen diesen
Wert: ϑ=a·ek·t+ϑZimmer.
Aus t=0 folgt ϑ=90°C, aus t=1 folgt ϑ=90°C-0,2·70°C=76°C.
Diese beiden Bedingungen gestatten es, die Parameter a und k zu
bestimmen. Dann kann auch leicht die gestellte Frage beantwortet werden.
- Lösung der Aufgabe:

Man muss also knapp 6 Minuten warten, bis der Kaffee die richtige
Temperatur hat.
- Hausaufgabe: Seite 169 Aufgabe 9
2016-01-14
- Übungsaufgaben zum beschränkten Wachstum.

- Eine Regression zum beschränkten Wachstum erlaubt der Taschenrechner
nicht.
Stattdessen geht man folgendermaßen vor:
Von den gegebenen Funktionswerten subtrahiert man den Wert S der
Sättigungsgrenze.
Auf die verbleibenden Werte kann man dann eine exponentielle Regression
anwenden.
Die gefundene Funktionsgleichung wird dann noch mit dem Wert S addiert.
- Beispiel:

Als Grenzwert S wird S=20 gesetzt.
Daraus ergibt sich:

Exponentielle Regression mit dem Taschenrechner durchführen:
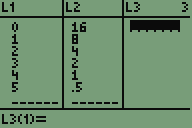



Es ergibt sich die Regressionsgleichung 20-f(t)=16∙0,5t und
daraus f(t)=20-16∙0,5t.
- Hausaufgabe:
Gegeben ist die Messreihe 
Die Bereiche von t=0 bis t=4 und von t=4 bis t=9 sollen getrennt auf
Wachstumsverhalten untersucht werden.
2016-01-19
- Lösung der Hausaufgabe:
- Zeichnen der Messpunkte:
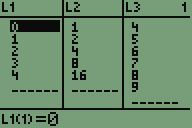
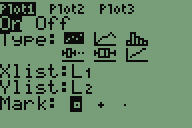



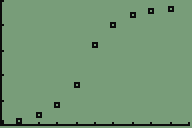
- Für t=0 bis t=4 Ansatz: exponentielles Wachstum (ExpReg)
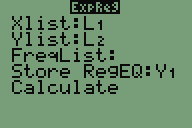


- Für t=4 bis t=9 Ansatz: begrenztes Wachstum
Da der Taschenrechner hierfür keine Regression anbietet, werden die
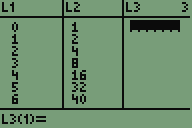
Differenzen von Funktionswert und Grenzwert berechnet (L5=48-L4).
Diese Werte sind Werte einer Exponentialfunktion, für die die
Regression ExpReg verwendet werden kann. Das Ergebnis wird unter Y2
gespeichert. Für die richtige Darstellung des Funktionsgraphs wird die
Differenzbildung rückgängig gemacht: Y3=S-Y2 mit S=48.

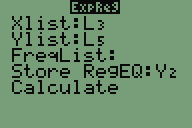



- In der Natur tritt häufig ein Wachstumsverhalten auf, das zunächst wie
ein exponentielles Wachstum und dann wie ein begrenztes Wachstum
erfolgt.
Bei Bäumen ist z. B. die Wachstumsgeschwindigkeit zur Zeit t oft
proportional zur Größe des Baumes und proportional zu der Länge, die an
der maximalen Höhe des Baumes noch fehlt.
Mit S als maximal möglicher Höhe des Baumes gilt dann für die
Wachstumsgeschwindigkeit (Ableitung der Höhe nach der Zeit):

- Der Taschenrechner bietet als Regression dazu "Logistic" an.
Die entsprechende Funktion für die Tabelle der Hausaufgabe:
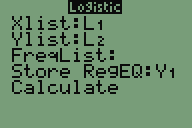


2016-01-21
- Wiederholung zum logistischen Wachstum an Hand der Besprechung der
Hausaufgabe (Seite 174 Aufgabe 6)
- Wiederholung Produktregel,
Quotientenregel
und Kettenregel
- Anwendung auf e-Funktionen in Verbindung mit einer Kurvendiskussion
2016-01-26
- Nach der Besprechung der Hausaufgabe Einführung in das Thema
Funktionsscharen am Beispiel der Funktion f(x)=ex-ax.
Nullstellen können nicht exakt ermittelt werden.
Näherungslösungen kann man aber leicht mit Hilfe des Taschenrechners
erlangen: MATH > SOLVER.
Siehe dazu die Anleitung unter TI-84-Funktionen
auf Seite 3.
2016-02-02
- Besprechung von Ortskurven
und Schnittstellen bei Funktionsscharen.
2016-02-04
- Wiederholung zur Klausur 3
- Beispielaufgabe:
Gegeben ist eine Funktionenschar. Gesucht sind die Ortskurve der
Extrempunkte und Punkte, in denen sich zwei beliebige Graphen der Schar
schneiden.

Die Ortskurve hat die Gleichung y=0,5∙x (Ursprungsgerade mit Steigung
0,5)
Unabhängig vom Wert des Parameters schneiden sich alle Kurven der Schar
im Punkt (0/0).
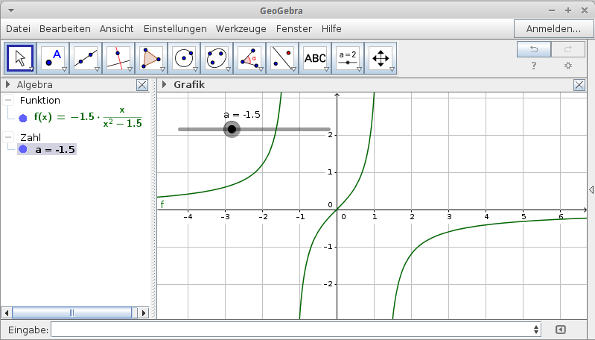
GeoGebra-Datei zum download.
Screenshots:

2016-02-09
2016-02-11
- Besprechung der Klausur 3
- Ableiten und Integrieren der allgemeinen Exponentialfunktion:

2016-02-16
- Rückgabe der Klausur 3 [ Aufgaben
| Lösungen
]
- Wiederholung zum Abitur: Ableitung, Ableitungsregeln
2016-02-18, 2016-02-23, 2016-02-25, 2016-03-01, 2016-03-03, 2016-03-08
2016-03-10
- Zeugnisnotenbesprechung und letzte Wiederholung zum Abitur. Viel
Erfolg bei den Prüfungen!