Unterrichtseinsichten
- Schuljahr 2008/2009 - Physik 7d
Optik
2009-01-26
- Schülerversuch zur Lichtausbreitung
- Aus einer Experimentierleuchte tritt das Licht durch eine Blende mit 5 Schlitzen heraus.

Man sieht, dass sich das Licht geradlinig ausbreitet. - Wegen
der geradlinigen Lichtausbreitung kann man den Entstehungsort des
Lichtes konstruieren, indem man die Lichtwege nach links fortsetzt:
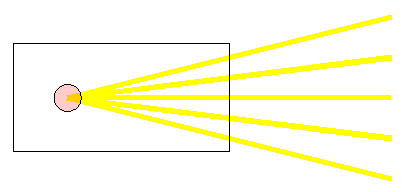
Den Ort der Lampe erkennt man am Schnittpunkt der Lichtwege.
Ein Vergleich mit der Experimentierleuchte bestätigt die durch Konstruktion gefundene Lage.
2009-01-29
- Im Versuch habt Ihr erkannt:
- An den Stellen, an denen das Licht einer einzigen Lampe ankommt, ist es hell.
Die Stellen, die von beiden Lampen beschienen werden, sind heller.

- Wird
in den Lichtkegel einer Lampe ein undurchsichtiger Gegenstand gestellt,
so kommt hinter dem Gegenstand kein Licht an. Dort ist Schatten.

Um
den Ort des Schattens auf dem Schirm zu finden, zeichnet man die
Randstrahlen am gegenstand entlang. Zwischen den Randstrahlen ist dann
auf dem Schirm der Schatten.
- Festlegungen
- Ein Lichtstrahl ist der Weg, auf dem sich das Licht ausbreitet. Ein Weg ist aber nur eine gedachte Linie.
Spricht man vom Licht, das aus einer Taschenlampe kommt, sollte man deshalb nicht vom "Lichtstrahl der Taschenlampe", sondern z. B. vom "Lichtbündel der Taschenlampe" sprechen. - Wenn nicht anders vereinbart, ist der Ursprung des Lichtes einer Lampe immer in einem einzigen Punkt.
Verwendet man das Schaltzeichen  für eine Lampe, so stammt alles Licht genau aus dem Schnittpunkt der beiden schrägen Strecken.
für eine Lampe, so stammt alles Licht genau aus dem Schnittpunkt der beiden schrägen Strecken.
2009-02-06
- Lernzielkontrolle zum Thema "Elektrizität"
2009-02-09
2009-02-13
- Schülerversuch: Die Lichtkegel zweier Lampen kreuzen sich. im gemeinsam beschienenen Teil befindet sich ein Gegenstand.
Markiere die Ränder der verschieden hellen Bereiche. - Vereinfacht gezeichnet sehen Eure Versuchsergebnisse so aus:
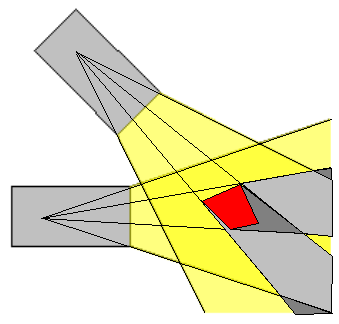
Erläuterungen zur Skizze: - Die in die Lampe hinein verlängerten Lichtstrahlen schneiden sich am Ort der Glühlampe.
- Der Gegenstand im Strahlengang ist rot gezeichnet.
- Die Randstrahlen am Gegenstand teilen das beleuchtete Gebiet in verschiedene Abschnitte.
- Orte, an denen ein Kernschatten (=hier kommt kein Licht an) vorliegt, sind dunkelgrau gezeichnet.
- Orte, an denen ein Halbschatten (=hier kommt nur das Licht einer einzigen Lampe an) vorliegt, sind hellgrau gezeichnet.
- GeoGebra-Arbeitsblatt von Schüler Mirco (Notebook-Klasse) zum Thema Kern- und Halbschatten.
- Link zu weiteren Schattenarten.
2009-02-16
- Besprechung der Ergebnisse aus dem Schülerversuch der letzten Stunde.
- Beginn: Mondphasen
2009-02-20
2009-02-27
- Klärung von Fragen zu den Finsternissen und den Mondphasen.
- Wenn Ihr an Sonne, Mond und Sternen interssiert seid, empfehle ich Euch die Seite http://www.astronews.com/ . Dort gibt es jeden Tag die neuesten Informationen, die man sich auch mit einem Newsletter per e-Mail schicken lassen kann.
- Vorbereitung des Schüler-Versuchs zum Thema Lochkamera.
2009-03-02
- Schülerversuch zum Thema Lochkamera.
Ihr habt alle das umgedrehte L gesehen. - "Schönere" Bilder werdet Ihr erzeugen, wenn Ihr als Hausaufgabe selbst eine Lochkamera nach der Vorlage gebaut habt.
Setzt Euch in ein dunkles Zimmer, möglichst weit vom Fenster entfernt und richtet die Lochkamera auf das Fenster.
Ich wünsche Euch eine schöne Fern-Seh-Zeit.
2009-03-06
- Einige
haben sehr schöne Lochkameras gebastelt! Bitte verbessert und
verschönert Eure Kameras, damit wir sie am Tag der offenen
Tür ausstellen können!
- Die Abhängigkeit zwischen
Schärfe und Helligkeit des Bildes und der Größe der
Kamera-Öffnung kann man an folgender GeoGebra-Simulation experimentell erforschen:
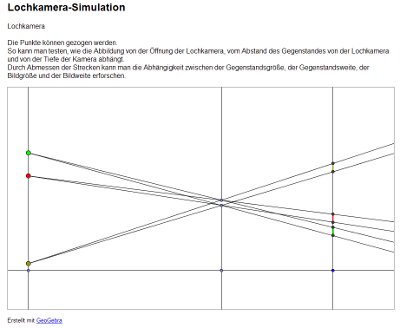
- An
der Simulation kann man auch die Abhängigkeiten von
Gegenstandsgröße G, Gegenstandsweite g, Bildgröße
B und Bildweite b erkennen.
Im Unterricht haben wir schon gesehen: G~g, B~b.
Weitere Zusammenhänge werden wir in der nächsten Stunde besprechen.
2009-03-09
- Mit diesem GeoGebra-Arbeitsblatt
haben wir durch Abmessen von g, G, b und B und Vergleichen der
Messwerte Gesetzmäßigkeiten bei der Abbildung mit der
Lochkamera gefunden.
Es gilt z. B. die Formel B/G=b/g. Wenn man 3 Werte in dieser Formel kennt, kann man den vierten Wert berechnen.
2009-03-13
- Wiederholung zur Abbildungsformel B/G=b/g.
- Mit
der Magntettafeloptik haben wir eine Messreihe aufgenommen, die uns
angibt, wie ein Lichtstrahl an einem Spiegel reflektiert wird.
Wir haben den Einfallswinkel α (Winkel zwischen dem ankommenden Lichtstrahl und der Senkrechten zum Spiegel) und
den Ausfallswinkel β (Winkel zwischen der Senkrechten zum Spiegel und dem reflektierten Lichtstrahl) gemessen.
- Versuchsaufbau:

- Messreihe:

- Hausaufgabe: Winkel zwischen einfallendem und ausfallendem Lichtstrahls berechnen.
2009-03-16
- Ergebnisse der Auswertung der Messergebnisse aus der letzten Stunde

- Im Experiment haben wir gesehen: Wenn man sich nicht ganz in einem
Spiegel sehen kann, hat es keinen Zweck, näher an den Spiegel zu gehen
oder sich vom Spiegel zu entfernen. Immer sieht man nur den selben
Ausschnitt von sich selbst.
- Wie groß muss denn ein Spiegel sein, damit man sich ganz darin sehen kann?
Auf diese Frage haben die meisten geantwortet: "So groß, wie man selbst ist."
Ob das zutrifft, sollt Ihr selbst zu Hause herausfinden.
2009-03-20
- Die
Besprechung der Hausaufgabe ergab: Ein Spiegel muss halb so groß
sein wie man selbst, damit man sich ganz darin sehen kann.
Erkunden kann man diesen Zusammenhang mit diesem GeoGebra-Arbeitsblatt:

- Wie liegt das Bild eines Gegenstandes im Vergleich zum Gegenstand selbst zu einem Spiegel?
Bild
und Gegenstand haben jeweils den gleichen Abstand zum Spiegel und die
Verbindungslinie zwischen Gegenstand und Bild steht senkrecht auf dem
Spiegel.
Auch dieser Zusammenhang lässt sich an einem GeoGebra-Arbeitsblatt untersuchen:
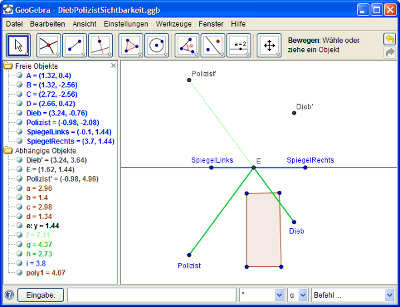
2009-03-23
- Wir haben einen Zaubertrick kennengelernt: Häufig werden Spiegel eingesetzt, um die Zuschauer zu täuschen.
Unser Beispiel: Die unter Wasser brennende Kerze.
Konstruktion
der Strahlengänge bei diesem Versuch: Spiegelt man die Kerze am
Spiegel, so ist das Bild am Platz der im Wasser befindlichen Kerze.
Vom
gespiegelten Punkt zeichnet man eine Verbindungsstrecke zum Auge, dann
eine Strecke vom Schnittpunkt Verbindungsstrecke-Spiegel zur Kerze
(siehe Bild am 2009-03-20).
2009-04-17
- Wiederholung zur Reflexion von Lichtstrahlen
- Zur Sichtbarkeit in Spiegeln: Randstrahlen zeichnen
- Anwendung des Reflexionsprinzips in anderen Zusammenhängen (Minigolf, Billard)
2009-04-27
2009-05-04
2009-05-08
- Besprechung und Rückgabe der Klassenarbeit 2 [ Aufgaben | Lösungen ]
- Beginn: Reflexion am Hohlspiegel
2009-05-11
- Schülerversuch zum Thema Brechung des Lichts:
Ein schmales Lichtbündel wird durch einen Glaskörper (Trapez-Grundriss) geleitet. Der Lichtweg wird notiert.
Die Auswertung werden wir in der nächsten Stunde vornehmen.
2009-05-14
- An der Magnettafeloptik haben wir den Schülerversuch vom letzten Mal nachgestellt und besprochen.
Ergebnisse: - Trifft
das Lichtbündel auf einen Glaskörper mit parallelen
Wänden, so sind die Lichtwege vor und hinter dem Glaskörper
parallel zueinander.
- Trifft das Lichtbündel auf eine
einzelne Grenzschicht zwischen Luft und Wasser, so wird das Licht
aus seiner Richtung abgelenkt, es wird gebrochen. Versuch: Fische
stechen.
- Ihr habt die Frage gestellt, ob es zwischen dem
Winkel des einfallenden Lichts und dem Winkel des gebrochenen Lichts
einen Zusammenhang gibt.
Das werden wir in der nächsten Stunde in einem Schülerversuch untersuchen.
2009-05-18
- Schülerübung zum Thema: Brechung des Lichts

Gemessen wurde im Schülerversuch der Einfalls- und der Ausfallswinkel beim Übergang von Luft zu Glas.
Im Bild erkennt man, dass bei einem Einfallswinkel von 30° der Ausfallswinkel den Wert 20° hat. - Die Tabellen und Grafiken, die Ihr mit Eurem Taschenrechner erstellt habt, werden wir in der nächsten Stunde besprechen.
2009-05-25
- Die in der letzten Stunde gemessenen Werte haben wir im Taschenrechner in die Listen L1 und L2 eingegeben:

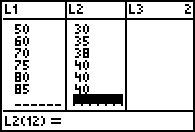

Da
Ihr vermutet habt, dass Einfalls- und Ausfallswinkel proportional
zueinander sind, haben wir mit STAT > CALC > LinReg(ax+b)
L1,L2,Y1 den Taschenrechner eine Gerade durch die Punkte legen lassen:
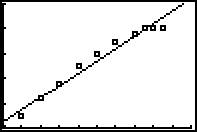
Man sieht deutlich, dass die Punkte nicht auf einer Geraden liegen, sondern auf einer gekrümmten Kurve.
Passt man nur die ersten Punkte an eine Gerade an, so ergibt sich:

Zunächst
scheinen die Punkte also auf einer Geraden zu liegen und dann für
große Einfallswinkel sanft abzuknicken.
Diese Gesetzmäßigkeit sollten wir uns so merken.
Später
(in den nächsten Schuljahren) lernen wir dann die mathematische
Funktion kennen, die hinter dem "richtigen" Kurvenverlauf steckt
(Sinuskurve y = sin x).
Hier ein Bild einer Sinuskurve. Der umrandete Bereich beschreibt unser Versuchsergebnis:

2009-06-05
- Am
2009-05-18 hatten wir einen Versuch zur Licht-Brechung
durchgeführt und dabei einen Lichtstrahl auf die Mitte der geraden
Seite eines Halbzylinders fallen lassen.
Wir haben gesehen, dass das Licht zum Einfallslot hin gebrochen wird.
In
dieser Stunde wurde der umgekehrte Lichtweg gewählt: Das Licht
fällt senkrecht auf die gekrümmte Fläche des
Halbzylinders und tritt in der Mitte der geraden Kante des
Halbzylinders wieder aus.
Einfallswinkel (innerhalb des Halbzylinders) und Ausfallswinkel wurden gemessen. Hier einige Beispiele:




Man
erkennt, dass der Einfallswinkel immer kleiner ist als der
Ausfallswinkel (wegen des Prinzips der Umkehrbarkeit des Lichtweges ist
das auch verständlich - siehe vorletzte Stunde).
Wird der
Einfallswinkel immer größer, müsste der Ausfallswinkel
irgendwann größer als 90° sein. Das geht aber nicht, da
dann das Lichtbündel nicht aus dem Glas austreten kann.
Einfach
verschwinden kann das Lichtbündel aber auch nicht an der
Grenzfläche, da die Energie des Lichtes irgendwo bleiben muss.
Bei
zu großen Einfallswinkeln wird das Licht nicht mehr nach
außen gebrochen, sondern zurück ins Glas reflektiert nach
der Gesetzmäßigkeit Einfallswinkel=Ausfallswinkel. - Folgende "Entwicklung" kann man bei größer werdendem Einfallswinkel beobachten:
- Bei
kleinen Einfallswinkeln (z.B. 20°, Foto oben links) wird fast alles
Licht gebrochen (hier Ausfallswinkel 30°) und fast kein Licht
reflektiert.
- Bei größeren Einfallswinkeln (z.B.
40°, Foto oben rechts) wird das gebrochene
Lichtbündel schwächer und das reflektierte
Lichtbündel stärker.
- Bei etwa 42° (Foto unten
links) ist der Ausfallswinkel fast 90° und das gebrochene Licht
fast nicht mehr zu erkennen. Dafür ist das reflektierte Licht sehr
gut zu sehen.
- Über 42° Einfallswinkel (z.B. 50°,
Foto unten rechts) wird das Licht nicht mehr gebrochen, sondern
vollständig reflektiert. Die Intensität des reflektierten
Lichts ist genau so groß wie die Intensität des einfallenden
Lichtes. Diesen Effekt der vollständigen Reflexion nennt man Totalreflexion. Simulation zur Totalreflexion.
- Anwendungen zur Lichtbrechung und Totalreflexion (unter Ausblicke).
2009-06-08
- Anwendungen der Totalreflexion
u.a. Lichtleiter: Führung eines Laserlichtbündels durch einen ausfließenden Wasserstrahl.

2009-06-12
- Schülerversuch zur Brechung an Linsen.



- Aufgabe:
Untersuche bei verschiedenen Linsenformen, wie parallel einfallende
Lichtbündel an den Linsen gebrochen werden. Was ist gleich? Was
ist unterschiedlich?
- Ergebnisse:
- Parallel einfallende Lichtbündel werden hinter der Linse in einem einzigen Punkt gesammelt.
- Je mehr die Linse gebogen ist, desto näher liegt dieser Sammelpunkt an der Linse.
- Anwendung:
Wird das Sonnenlicht durch eine Linse gesammelt, ist die Lichtenergie
in dem Sammelpunkt so stark, dass Papier dadurch entzündet werden
kann.
Dank an Kevin für einen Teil seines Arbeitsblattes.
Vorsicht!
Nicht zu Hause nachmachen! Linsen (auch Flaschen, Glasscherben,
Vergrößerungsspiegel usw.) auch nie einfach so herum liegen
lassen. Durchfallendes Sonnenlicht kann zu einem Brand führen! - Da draußen die Sonne sehr hell schien, mussten wir die Jalousien herunterlassen.
Durch
die Löcher in den Lamellen strahlte das Sonnenlicht und erzeugte
wie bei einer Lochkamera auf dem Fußboden Bilder der Sonne
(sogenannte Sonnentaler).

Unten etwas näher fotografiert.
Man erkennt die kreisförmigen Sonnenbilder,
Bilder von Fusseln an den Lamellen und
Nebenbilder,
die daher kommen, dass das Licht an den doppel-verglasten
Fensterscheiben mehrfach reflektiert und dabei etwas seitlich
verschoben wird.

2009-06-15
- An
folgendem Modell aus 2 Prismen mit einem gleichschenkligen Dreieck als
Grundfläche, zwei Prismen mit einem Trapez als Grundfläche
und einem Quader haben wir uns klar gemacht, wie bei einer Linse das
Sammeln der parallel einfallenden Strahlen im Brennpunkt erfolgt:

- Hält
man eine Sammellinse so, dass das Licht, das durch ein Fenster in einen
Raum fällt, durch die Linse auf ein weißes Blatt Papier
fällt, so wird bei geeignetem Abstand zwischen Papier und Linse
das Fenster und draußen in der Helligkeit befindliche
Gegenstände auf dem Papier abgebildet:

- Wie kommt ein solches Bild zustande?
In folgender Zeichnung sind dargestellt die "optische Achse" und senkrecht dazu die (als unendlich dünn gedachte) Linse.
In einem beliebigen Punkt befindet sich ein Gegenstand, hier z.B. die Flamme einer Kerze.
Von den unendlich vielen Strahlen, die von der Flamme ausgehen, betrachten wir 3 besondere Strahlen:

- Parallelstrahl:
Ein zur optischen Achse paralleler Strahl wird an der Linse so
gebrochen, dass er auf der anderen Seite der Linse durch den Brennpunkt
F2 verläuft.
- Zentrumsstrahl: Ein Strahl, der
durch den Schnittpunkt von Linse und optische Achse verläuft (also
durch das Zentrum der Linse), ändert seine Richtung auf Grund der
Linse nicht.
- Brennpunktstrahl: Ein Strahl, der durch den Brennpunkt F1 verläuft, wird auf der anderen Seite der Linse zu einem Parallelstrahl.
- Alle 3 Strahlen treffen sich auf der rechten Seite in einem Punkt, dem Bildpunkt.
Man
kann rechnerisch zeigen (das ist aber nicht so einfach...), dass auch
alle anderen Strahlen, die von der Flamme ausgehen und durch die Linse
abgelenkt werden, durch den Bildpunkt verlaufen. - Den Abstand Brennpunkt-Linse nennt man "Brennweite f", den Abstand Gegenstand-Linse "Gegenstandsweite g".
- Hausaufgabe:
Wie ändert sich das Bild, wenn die Gegenstandsweite oder die
Brennweite geändert werden? Was ist, wenn a) g>f ; b)
g=f ; c) g<f ?
2009-06-16
2009-06-17
- Zu Farben gibt es seihr gute Seiten bei "Leifi":
















