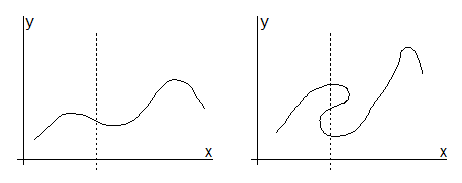Unterrichtseinsichten - Schuljahr 2008/2009 - Mathematik 7d

Lineare Funktionen

• Übungen zur Informationsgewinnung aus graphischen Darstellungen
• Fahrtenschreiber
• Zusammenhang zwischen dem Verlauf einer Rennstrecke und der Geschwindigkeit der Rennautos.

• Der Benzinverbrauch in Abhängigkeit von der gefahrenen Geschwindigkeit ist für 3 Autos gegeben: als Tabelle, als Graph und als Term
• Eure Aufgabe ist es, diese Informationen in einem einzigen Diagramm auf dem Taschenrechner darzustellen.
• In der nächsten Stunde werden wir die 3 Automodelle genauer untersuchen.

• Wir haben gelernt, wie man Punkte und einen Funktionsterm in einem Koordinatensystem darstellen kann.
  Anleitung dazu unter TI84-SekI.

• Häufig erleben wir, dass sich bei Änderung einer Größe eine andere Größe auch ändert.
  Beispiele:
• Im Ablauf der Zeit ändert sich draußen die Temperatur.
• Je nach Umfang eines Einkaufs muss man mehr oder weniger bezahlen.
• Je schneller ein Auto fährt, desto mehr Benzin wird verbraucht.
• Gibt es zwischen zwei Größen eine Regel, nach der die Werte der beiden Größen zusammen gehören, so spricht man bei dieser Beziehung von einer Relation.
• Gibt es bei einer Relation zu jedem Wert der veränderten Größe genau einen Wert der anderen Größe, so liegt eine besondere Relation vor, die man Funktion nennt.
• Beispiel:
  Geht man von zu Hause aus auf eine Wanderung und kommt am Ende der Wanderung nach zu Hause zurück, so liegt eine
• Relation vor, wenn man untersucht, wie groß der Abstand von zu Hause nach einer bestimmten Zeit ist
  (denn es gibt (fast) immer mindestens 2 verschiedene Zeiten, zu denen man die gleiche Entfernung bis nach Hause hat),
• Funktion vor, wenn man untersucht, wie lang die Strecke ist, die man nach einer bestimmten Zeit zurückgelegt hat
  (denn die Strecke nimmt kontinuierlich zu, falls man nicht gerade stehen bleibt).
• Häufig stellt man die Relation oder Funktion als Graph dar, wobei auf den Achsen des Koordinatensystems die betrachteten Größen abgetragen werden.
  Sind diese Größen x und y, so liegt 
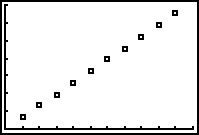
• links eine Funktion vor, da es zu jedem x-Wert genau einen y-Wert gibt und
• rechts eine Relation, da es zu einigen x-Werten mehr als einen y-Wert gibt (gestrichelte Linie).
  

• Eine Funktion kann man beschreiben durch
• eine Zuordnungsvorschrift
• eine Wertetabelle
• einen Funktionsgraphen
• Beispiel:
  Die Funktion f lässt sich beschreiben durch 
• x --> x²+1  oder y = x²+1 (wegen x --> y)
• 
• 
• Hausaufgabe: Seite 188 Aufgaben 13 und 17 a-d (1)

• Besprechung der Hausaufgabe
• Wir haben Folgendes gelernt:
• Setzt man in den Term -x² Zahlenwerte ein, so muss man erst die Zahlen quadrieren und danach das Vorzeichen beachten: -3²=-9 und -(-3)²=-9
• Es ist egal, wie man die Variable nennt: f(x)=(1-x)² ist dieselbe Funktion wie f(z)=(1-z)²
• Zeichnet man Funktionsgraphen, so darf man nicht die eingetragenen Punkte durch Strecken verbinden, sondern muss die Punkte mit einer möglichst glatten Kurve verbinden.
  Beispiel: Ihr habt zur Funktionsgleichung f(x)=-x² folgende Tabelle erstellt und dann diesen Graph gezeichnet:
    
  Der Graph kann nicht stimmen, denn wenn man die Wertetabelle um den x-Wert 0,5 ergänzt, so liegt der zugehörige Punkt F nicht auf dem Streckenzug:
   
  Zeichnet man dagegen einen gekrümmten Graphen ohne Knicke, so können alle berechneten Punkte auf dieser Linie liegen:
  
• Hausaufgabe:
• Berichtigung der Hausaufgabe
• Tabelle und Graph: Eine Pizza kostet 6,50 €. Die Tabelle und der Graph sollen anzeigen, wie viel eine beliebige Anzahl (zwischen 0 und 10) von Pizzen kostet.

• Die Lösung der Hausaufgabe (Kosten für Pizzen, jede Pizza kostet 6,50 €) bestand in einer Tabelle und dem zugehörigen Graph:
             
• Man sieht, dass die Punkte auf einer Ursprungsgerade liegen, also einer Geraden, die durch den Punkt (0/0) verläuft.
• Multipliziert man den x-Wert immer mit 6,5, so ergibt sich der y-Wert. Es gilt also y=6,5·x.
• Experimentell habt Ihr mit dem Taschenrechner erprobt, was für Graphen es gibt, wenn man statt 6,5 andere Werte einsetzt:
  
  Alle Graphen sind Geraden, die durch den Koodinatenursprung verlaufen.
  Allgemein schreibt man die Gleichung dieser Geraden mit y=m·x, wobei m irgendeine positive oder negative Zahl ist.
• Ihr habt gesehen: ist m positiv und sehr groß, so ist die zugehörige Gerade sehr steil und verläuft von links unten nach rechts oben.
  Wird m kleiner, so wird die Gerade flacher.
  Wird m negativ, so fällt die Gerade von links oben nach rechts unten ab.
• Hausaufgabe: Untersuche, für welche Werte von m die Ursprungsgerade in den Bereichen 1, 2, 3 und 4 verläuft:
  

• Besprechung der Hausaufgabe:
  In der Gleichung y=m·x der Ursprungsgerade nimmt m folgende Werte an:
• bei1:   m>1
• bei 2:   0<m<1
• bei 3:   -1<m<0
• bei 4:   m<-1
• Man kann das sehr einfach einsehen, indem man sich klar macht, dass für x=1 der y-Wert gleich dem m-Wert ist.
  Von der x-Achse bei 1 aus geht man senkrecht bis zur Gerade. Der y-Wert gibt dann den m-Wert an.
• Wenn man einen Punkt der Geraden kennt, kann man aber auch wegen y=m·x --> y/x=m einfach den y-Wert der Punktes durch den x-Wert dividieren und erhält den m-Wert.

• Ursprungsgeraden lassen sich durch die Gleichung y=m·x beschreiben.
• Andere Geraden haben die Gleichung y=m·x+b.
• m nennt man Steigung und b den y-Achsenabschnitt.
• Schaut Euch zur Wiederholung die folgenden Arbeitsblätter zur
  Ursprungsgerade      
  und zur
  allgemeinen Gerade  
  an und experimentiert mit den Geraden herum.
  Verändert die Steigung und den y-Achsenabschnitt und schaut Euch an, was das für einen Einfluss auf die Geradengleichung hat.
  Überlegt Euch auch, wie man von einer bekannten Gerade auf die entsprechende Gleichung und von einer bekannten Gleichung zur entsprechenden Gerade kommt.
• Hausaufgabe: Seite 207, Aufgabe 15 die ersten beiden Reihen

• Besprechung der Hausaufgabe und weitere Übungen zu den Themen
• Geradengleichung gegeben --> Graph zeichen
• Graph einer Gerade gegeben --> Funktionsgleichung finden
• Hausaufgabe: Seite 208 Aufgabe 18 ganz

• Wiederholung zur Geradengleichung:
  In der Gleichung y=m·x+b bedeutet:
• b : y-Achsenabschnitt, d.h. der Wert an der Stelle auf der y-Achse, an dem die Gerade die y-Achse schneidet
• m : Steigung der Gerade. Man findet den Wert, indem man beim Steigungsdreieck die Länge der senkrechten Strecke durch die Länge der waagrechten Strecke dividiert.
  Fällt die Gerade von links nach rechts nach unten ab, so ist der Steigungswert negativ, steigt die Gerade von links nach rechts an, so ist der Steigungswert positiv.
• Die Änderungsrate einer linearen Funktion ist die Steigung der Gerade. Man ermittelt sie, indem man zwischen 2 Punkten der Gerade ein Steigungsdreieck zeichnet und dann die Länge der senkrechten Strecke durch die Länge der waagrechten Strecke dividiert.

• Besprechung der Hausaufgabe: Geradengleichung bestimmen, wenn die Geraden gezeichnet vorliegen (siehe auch letzte Stunde).
• Berechnung der Geradengleichung, wenn nur die Koordinaten zweier Punkte gegeben sind und nicht gezeichnet werden soll:
  Um zu versetehen, was gemacht wird, hier doch mal eine Zeichung dazu:
  
  Die Punkte A(1/2) und B(5/4) sind gegeben. 
• Man rechnet in Gedanken aus, welche Seitenlängen das Steigungsdreieck hat, das mit Hilfe dieser beiden Punkte gezeichnet werden kann: 
• Senkrechte Strecke: y-Wert von B minus y-Wert von A gibt 4-2=2
• Waagrechte Strecke: x-Wert von B minus x-Wert von A gibt 5-1=4
• Man dividiert die Länge der senkrechten durch die Länge der waagrechten Strecke: 2/4=1/2=0,5 und erhält damit den m-Wert in der Gleichung y=m·x+b.
• Wir haben nun also schon einmal y=0,5·x+b. Das b erhält man, indem man die Koordinaten eines Punktes der Gerade für x und y einsetzt.
• Wählen wir den Punkt A (B geht genau so - bitte nachrechnen!), so gilt: 2=0,5·1+b  --->  2=0,5+b  --->  b=1,5
• Damit ergibt sich insgesamt die Gleichung y=0,5·x+1,5.

• Kann man so wie in der letzten Stunde immer eine Geradengleichung bestimmen, wenn die Koordinaten von 2 Punkten bekannt sind?
• Nehmen wir mal allgemein an, dass die Koordinaten der Punkte x₁, y₁, x₂ und y₂ heißen:  A(x₁/y₁) ; B(x₂/y₂).
• Man rechnet in Gedanken aus, welche Seitenlängen das Steigungsdreieck hat, das mit Hilfe dieser beiden Punkte gezeichnet werden kann: 
• Senkrechte Strecke: y-Wert von B minus y-Wert von A gibt y2-y1
• Waagrechte Strecke: x-Wert von B minus x-Wert von A gibt x2-x1
• Man dividiert die Länge der senkrechten durch die Länge der waagrechten Strecke:  und erhält damit den m-Wert in der Gleichung .
  Den Bruch nennt man auch "Änderungsrate", weil er ein Maß dafür ist, um wie viel sich der y-Wert (senkrecht) ändert, wenn sich der x-Wert (waagrecht) um einen bestimmten Wert ändert.
• Auch den b-Wert könnte man allgemein ausrechnen, was aber für die Klassenstufe 7 doch sehr schwer ist.
  Oder fühlt sich eine(r) von Euch fit für diese Rechnung? Probiert es doch mal!
  Das Ergebnis für b und die gesamte Geradengleichung seht Ihr zwischen < und >, wenn Ihr den Bereich dazwischen markiert.
  < b=(x₂·y₁-x₁·y₂)/(x₂-x₁)       Geradengleichung: y=(y₂-y₁)/(x₂-x₁)·x+(x₂·y₁-x₁·y₂)/(x₂-x₁)>
• Beispiel zur Berechnung der Geradengleichung, wenn folgende Punkte gegeben sind: A(-5/8) ; B(12/6)
• Mit x₁=-5, y₁=8, x₂=12, y₂=6 gilt  (y2-y1)/(x2-x1)=(6-8)/(12-(-5))=-2/17
• Vorläufige Geradengleichung: y=-2/17·x+b.
• x₁ und y₁ für x und y einsetzen: 8=-2/17·(-5)+b  --->  8=10/17+b   --->   136/17=10/17+b   --->   126/17=b
• Die Geradengleichung ist also  y=-2/17·x+126/17

• Das bisher Gelernte haben wir heute an einem Beispiel aus der Technik geübt:
  Brücken und Eisenbahngleise sind nicht immer gleich lang. Bei Erwärmung dehnen sie sich aus, bei Abkühlung ziehen sie sich zusammen. Man muss deshalb zwischen einzelnen Bauteilen Lücken (Dehnungsfugen) lassen, so dass für eine Ausdehnung Platz bleibt.
  Die Relation zwischen der Temperatur und der Breite der Dehnungsfuge ist ein linearer Zusammenhang, den man durch eine Geradengleichung beschreiben kann.
  Bekannt ist, dass die Dehnungsfuge bei 0°C eine Breite von 48mm und bei 25°C eine Breite von 28mm hat.
• Aufgaben dazu:
• Bestimme die Funktionsgleichung, die den Zusammenhang zwischen Temperatur und Breite der Dehnungsfuge beschreibt.
  Lösung:
• Allgemeine Geradengleichung: y=m·x+b
• x sei die Temperatur, y die Breite der Dehnungsfuge.
• Dann kennen wir die Koordinaten zweier Punkte (x/y) der Gleichung: (0/48) und (25/28).
• Änderungsrate m=(y₂-y₁)/(x₂-x₁)=(28-48)/(25-0)=-20/25=-4/5
• Der y-Achsenabschnitt b ergibt sich unmittelbar aus den Koordinaten des Punktes (0/48) zu 48
  (Man hätte auch die Koordinaten eines Punktes in die vorläufige Gleichung y=-4/5·x+b einsetzen und so b berechnen können)
• Damit ist die Gleichung gefunden: y=-4/5·x+48
• Welche Breite hat die Dehnungsfuge bei den Temperaturen 30°C und -15°C?
  Lösung:
• Die jeweilige Temperatur wird als x-Wert in die Gleichung eingesetzt und y(=Breite) wird berechnet.
  30°C: y=-4/5·30+48=-24+48=24         Bei 30°C beträgt die Breite 24mm.
  -15°C: y=-4/5·(-15)+48=12+48=60       Bei -15°C beträgt die Breite 60mm.
• Bei welcher Temperatur hat die Dehnungsfuge eine Breite von 54mm?
  Lösung:
• Die Breite wird als y-Wert in die Gleichung eingesetzt und der x-Wert (=Temperatur) wird berechnet.
  54=-4/5·x+48   --->   54-48=-4/5·x   --->   6=-4/5·x   --->   30/(-4)=x   --->   x=-7,5      Die Breite 54mm misst man bei -7,5°C.
• Bis zu welcher Temperatur erfüllt die Dehnungsfuge ihren Dienst?
  Lösung:
• Die Breite der Dehnungsfuge muss einen positiven Wert haben. Der kleinste Wert kann die 0 sein. Dieser Wert wird für y eingesetzt.
  0=-4/5·x+48   --->   -48=-4/5·x   --->   48·5/4=x   --->   60=x
  Bei einer Temperatur von 60°C ist die Dehnungsfuge geschlossen. Bei höheren Temperaturen können die Bauteile zerstört werden.
  Da in Deutschland Lufttemperaturen von über 60°C nicht vorkommen, ist die Breite der Dehnugsfuge ausreichend gewählt.

• Übungen und Wiederholungen zur Klassenarbeit 5 am 2009-05-27

• Klassenarbeit 5

• Besprechung und Rückgabe der Klassenarbeit 5 [ Aufgaben | Lösungen ]

• In den letzten Stunden haben wir gelernt, wie man eine Geradengleichung findet, deren Graph (nämlich die Gerade) exakt durch 2 Punkte verläuft.
• Bei Messungen gibt es häufig das Problem, eine Gerade (Ausgleichsgerade genannt) durch viele Punkte legen zu müssen, obwohl die Punkte nicht exakt auf einer Geraden liegen.
  Man kann eine solche Gerade so "nach Gefühl" durch die Punktemenge legen, dass es "am besten passt". Das Ergebnis kann dabei sehr unterschiedlich ausfallen.
• Es gibt aber auch Vorschriften für das Aufstellen der Geradengleichung, so dass verschiedene Anwender genau dieselbe Geradengleichung finden.
  Eine dieser Methoden ist das Suchen der Mediangerade.
  Zur Vorbereitung haben wir heute eine Punktwolke zu folgender Tabelle gezeichnet:
  
  
• Um die Mediangerade zu finden, werden zunächst die Punkte in x-Richtung sortiert in 3 Bereiche mit jeweils gleich viel Punkten zusammengefasst.
  Falls die Anzahl der Punkte nicht durch 3 zu teilen ist (wie in diesem Fall), achtet man darauf, dass die beiden äußeren Bereichegleich viele Punkte enthalten.
• In der nächsten Stunde werden wir hier weiter arbeiten.

• Fortsetzung der letzten Stunde:
• In jedem Bereich suchen wir nun den Median-Punkt: Wir sortieren die x-Werte und die y-Werte und nehmen jeweils den Wert, der genau in der Mitte liegt.
  Ist die Anzahl der Punkte geradzahlig, nehmen wir den Mittelwert der beiden mittleeren Punkte.
  Es ergibt sich im roten Bereich: (40/27), im gelben Bereich: ((60+65):2/(30+30):2) = (62,5/30), im grünen Bereich: (85/34).
• Nun wird die Steigung der Gerade berechnet, die durch die beiden äußeren Punkte verläuft:
  m=(y3-y1)/(x3-x1)=(34-27)/(85-40)=7/45.
• Durch jeden der 3 Punkte wird eine Gerade mit der eben berechneten Steigung gelegt und deren y-Achsenabschnitt bestimmt:
• links: y₁=7/45·x+b₁ ---> 27=7/45·40+b₁ ---> b₁=27-56/9 ---> b₁=243/9-56/9=187/9 ---> y₁=7/45·x+187/9
• Mitte: y₂=7/45·x+b₂ ---> 30=7/45·62,5+b₂ ---> b₂=30-9,722 ---> b₂=20,28 ---> y₂=7/45·x+20,28
• rechts: y₃=7/45·x+b₃ ---> 34=7/45·85+b₃ ---> b₃=34-119/9 ---> b₃=306/9-119/9=187/9 ---> y₃=7/45·x+187/9
• Der Mittelwert der 3 y-Achsenabschnitte wird berechnet: (187/9+20,28+187/9)/3=20,61 und ergibt den y-Achsenabschnitt der Median-Geraden.
• Die Gleichung der Mediangeraden ist y=7/45·x+20,61

• Ermitteln der Mediangerade mit dem GTR:
     
  
     
  
  Zunächst gibt man in den Listen L1 und L2 die Tabellenwerte ein.
  Mit STAT > CALC > Med-Med und anschließend eingegebenen L1, L2, Y1 und ENTER erhält man die Lösung y=0,16·x+20,61.