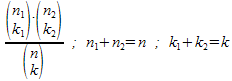Unterrichts-Einsichten - Schuljahr 2007/2008 - Mathematik 10c
Datenanalyse mit Bernoulli-Versuchen
2007-11-07
- Im
Zusammenhang mit der Besprechung der Hausaufgabe haben wir uns über das
Dualsystem unterhalten und gesehen, wie man Dualzahlen addieren und
multiplizieren kann.
Wer mehr darüber wissen möchte,
kann sich ja mal die Dokumentation meines Informatikunterrichts
ansehen: Grundkurs
Informatik im Schuljahr 2001/2002. - Bei
allen Teilaufgaben haben wir gsehen, dass trotz unterschiedlicher
Elemente (Münzen, Personen, Dualzahlen usw.) immer dasselbe Ergebnis
herauskam.
In der Mathematik versucht man, die Strukturen
hinter den Anwendungen zu erkennen.
Bei dieser
Aufgabe ging es darum, dass man "Dinge" betrachtet, die 2 verschiedene
Eigenschaften haben.
Die
Frage war nun, wie viele Möglichkeiten es gibt, wenn man 5 "Dinge"
nacheinander wählt, zum Schluss 3 "Dinge" einer bestimmten Eigenschaft
dabei zu haben.
Wenn Ihr dieses allgemeine Problem gelöst
habt, habt
Ihr eigentlich auch schon alle anderen Aufgaben gelöst. Das werden wir
in der nächsten Stunde noch einmal genauer sehen.
2007-11-08
- Man
hat 5 Plätze und möchte darauf 3 gleichartige Dinge ablegen. Was das
für "Plätze" sind und wie die "Dinge" aussehen, spielt keine Rolle.
Dann
hat man für das 1. Ding 5 Möglichkeiten, einen Platz auszusuchen.
Für
das 2. Ding bleiben dann noch 4 Möglichkeiten, weil ja ein Platz schon
belegt ist.
Für das 3. Ding bleiben nur noch 3 Möglichkeiten,
weil ja schon 2 Plätze belegt sind.
Insgesamt hat man also
5·4·3=60 Möglichkeiten, die 3 Dinge auf 5 Plätze zu verteilen. - Nun
sind die 3 Dinge aber gleichartig, d. h. ununterscheidbar.
Eine
Anordnung wie X_XX_ lässt
sich von X_XX_ oder X_XX_
unterscheiden, weil die X sich durch ihre Farbe unterscheiden.
Bei
gleichfarbigen X kann man aber zwischen den 3 Anordnungen keinen
Unterschied feststellen.
Die
oben berechnete Anzahl muss man also verkleinern. Dazu muss man
herausfinden, wie viele Arten es gibt, die 3 X auf die 3 Plätze zu
verteilen.
Für das 1. X hat man 3 Möglichkeiten, für das 2. X
nur noch 2 Möglichkeiten und für das letzte X ist nur noch 1 Feld frei.
Man
hat also 1·2·3=6 Möglichkeiten die 3 X auf die richtigen Plätze zu
verteilen.
Die
60 Möglichkeiten von oben muss man also durch 6 teilen, um die Anzahl
aller unterscheidbaren Anordnungen zu bekommen: 60/6=10 - Es
gibt also 10 unterschiedlich aussehende Möglichkeiten, 3 gleichartige
Dinge auf 5 Plätze zu verteilen.
- Alles
zusammengefasst in einem einzigen Term:

- Vorüberlegung für
Weihnachten:
Man
hat am Weihnachtsbaum 27 Stellen gefunden, an denen man 12 identische
Kerzenhalter befestigen kann. Wie viele Möglichkeiten gibt es für das
Schmücken des Baumes?
Wie oben für einen einfacheren Fall
gezeigt findet man hier das Ergebnis zu 
Ihr
seht: bei größeren Zahlen ist das Aufschreiben des Bruchs sehr
umständlich. Man hat deshalb nach einer vereinfachten Schreibweise
gesucht und dazu folgendes festgelegt:
1·2·3·4=4!
oder allgemein 1·2·3·4· ... ·n=n!
Man
liest die rechten Seiten der Gleichungen als "4 Fakultät" bzw. "n
Fakultät".
n ist immer eine ganze positive Zahl und n! ist das
Produkt aus allen positiven ganzen Zahlen, die kleiner oder gleich n
sind.
Den Nenner des riesigen Bruches kann man also als 12!
schreiben.
Der Zähler ist leider nicht 27!, weil alle Faktoren
von 1 bis 15 fehlen. Die fehlenden Faktoren kann man als 15! schreiben.
Also
gilt für den großen Bruch 
Man schreibt auch kürzer  , nennt die rechts stehende Klammer "Binom"
(von bi = zwei und nomos = der Name) und spricht es "27 über 12" aus.
, nennt die rechts stehende Klammer "Binom"
(von bi = zwei und nomos = der Name) und spricht es "27 über 12" aus. - Allgemein
gilt: Werden k ununterscheidbare Dinge auf n Plätze verteilt, gibt es
dafür
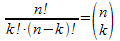 Möglichkeiten. Aussprache: "n über k"
Möglichkeiten. Aussprache: "n über k" - Sind
die "Dinge" identisch mit den "Plätzen", die man auswählt, sagt man
auch "Wähle k aus n mit einem Griff"
2007-11-09
- Die
Besprechung der Hausaufgabe ergab, dass noch Schwierigkeiten bestehen
beim Unterscheiden folgender Fälle (hier am Beispiel des Urnenmodells):
- Ziehen mit Zurücklegen
Eine
Kugel wird gezogen, die Zahl wird aufgeschrieben und dann wird die
Kugel wieder zurückgelegt. Danach zieht man die nächste Kugel und geht
genauso vor.
Es kommt darauf an, in welcher Reihenfolgen die
einzelnen unterscheidbaren Kugeln gezogen wurden.
Beispiel:
Eine Urne enthält 5 Kugeln, die mit 1 bis 5 beschriftet sind. Man zieht
3 Kugeln mit Zurücklegen. Jedes Mal hat man 5 Möglichkeiten, eine Kugel
zu ziehen, insgesamt also 5·5·5=125 Möglichkeiten.
Allgemein:
Eine
Urne enthält n Kugeln, die von 1 bis n beschriftet sind. Man zieht k
Kugeln mit Zurücklegen. Jedes Mal hat man n Möglichkeiten, eine Kugel
zu ziehen, insgesamt also  Möglichkeiten.
Möglichkeiten. - Ziehen ohne Zurücklegen
Eine
Kugel wird gezogen, die Zahl wird aufgeschrieben und die Kugel
wird zur Seite gelegt. Danach zieht man die nächste Kugel und geht
genauso vor.
Es kommt darauf an, in welcher Reihenfolgen die
einzelnen unterscheidbaren Kugeln gezogen wurden.
Beispiel:
Eine Urne enthält 5 Kugeln, die mit 1 bis 5 beschriftet sind. Man zieht
3 Kugeln ohne Zurücklegen. Beim 1. Mal hat man 5 Möglichkeiten, eine
Kugel
zu ziehen, beim 2. Mal nur noch 4 Möglichkeiten und beim 3. Mal nur 3
Möglichkeiten, insgesamt also 5·4·3=60 Möglichkeiten.
Allgemein:
Eine Urne enthält n Kugeln, die von 1 bis n beschriftet
sind. Man zieht k Kugeln ohne Zurücklegen. Jedes Mal hat man eine
Möglichkeit weniger, eine Kugel zu ziehen, insgesamt also  Möglichkeiten.
Möglichkeiten. - Ziehen mit einem GriffAlle
zu ziehenden Kugeln werden mit einem Griff gezogen. Man kann die Kugeln
auch nacheinander ziehen, aber dann auf die Reihenfolge nicht achten.
Die Reihenfolge, in der die Kugeln gezogen werden, ist also beliebig
(siehe auch Text zum 2007-11-08).
Beispiel: Eine Urne enthält
5
Kugeln, die mit 1 bis 5 beschriftet sind. Man zieht
3 Kugeln mit einem Griff (oder achtet einfach nicht auf die
Reihenfolge, in der man die Kugeln gezogen hat). Insgesamt hat man
dann  Möglichkeiten, verschiedene Ergebnisse zu
erhalten.
Möglichkeiten, verschiedene Ergebnisse zu
erhalten.
Allgemein: Eine Urne enthält n Kugeln, die von 1 bis
n beschriftet
sind. Man zieht k Kugeln mit einem Griff. Dann hat man 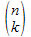 Möglichkeiten für unterschiedliche Ergebnisse.
Möglichkeiten für unterschiedliche Ergebnisse.
- Pascalsches Dreieck
In
folgendem Dreieck ergeben sich die Zahlenwerte dadurch, dass bei den
äußeren schrägen Begrenzungen überall 1 steht. Die anderen Zahlen
ergeben sich durch Addition der beiden schräg darüber stehenden Zahlen.
In der nächsten Stunde werden wir das Pascalsche Dreieck genauer
untersuchen.
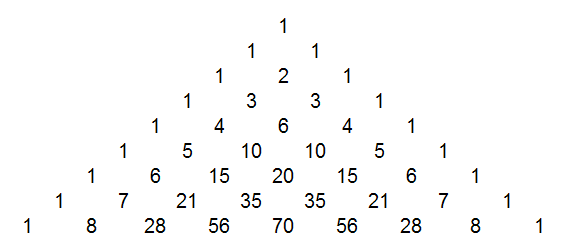
2007-11-12
- Wir
haben entdeckt, dass die Zahlen des Pascalschen Dreiecks mit den
Koeffizienten übereinstimmen, die beim Ausmultiplizieren von Termen der
Art
 entstehen:
entstehen:
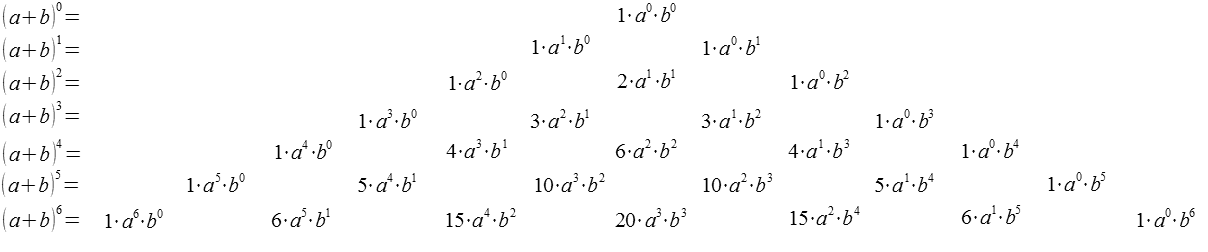
Die Hochzahlen der a- und
b-Faktoren addieren sich in einer Reihe immer zum selben Wert
(Hochzahl der Klammer).
Die Hochzahlen des a-Faktors nehmen
nach rechts hin ab, die des b-Faktors nach rechts hin zu. - Die
Zahlen des Pascalschen Dreiecks lassen sich durch Binome (siehe
2007-11-08) darstellen:

Wenn
man mit den Klammerausdrücken vergleicht, sieht man, dass oben in den
Binomen die Hochzahl an der Klammer und unten die Hochzahl der b steht. - Neben
der Definition
 für n>0 und k<=n ist nach dem
Pascalschen-Binom-Dreieck auch noch sinnvoll zu definieren
für n>0 und k<=n ist nach dem
Pascalschen-Binom-Dreieck auch noch sinnvoll zu definieren  , wobei man auf den Wert 0!=1 durch
folgende Überlegung kommt:
, wobei man auf den Wert 0!=1 durch
folgende Überlegung kommt:

Von einer Zeile kommt man zur
darunter stehenden Zeile, indem man durch die Zahl vor dem ! dividiert.
2007-11-14
- In
Erweiterung zur Berechnung der Wahrscheinlichkeiten beim Lotto haben
wir folgende Formel kennengelernt:
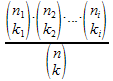
Diese Formel kann man benutzen,
wenn folgende Dinge gegeben bzw. gesucht sind:- Es
gibt insgesamt n Dinge, von denen man k Dinge mit einem Griff zieht.
- Die
n Dinge unterscheiden sich in i Merkmalen, wobei nj
Dinge das j-te Merkmal haben.
- Von den Dingen des
j-ten Merkmals zieht man kj Dinge mit einem
Griff.
- Im Nenner des Bruchs steht die Anzahl aller
Möglichkeiten, mit denen man k Dinge aus n Dingen mit einem Griff
ziehen kann.
- Im Zähler steht die Anzahl der
Ergebnisse, auf die es ankommt (die "gut" sind).
- Da
die Formel sehr abstrakt ist, hier ein Beispiel:
Bei einem Ausstellungs-Besuch
des gesamten 10. Jahrgangs nehmen 100 Personen teil: 40 Schüler, 50
Schülerinnen, 10 Lehrkräfte.
Alle Teilnehmer dürfen ein Los
ziehen. Als Preis winken 10 mathematische
Geduldsspiele.
Wie
groß ist die Wahrscheinlichkeit, dass (gerechter Weise?!) 4 Schüler
(m), 5 Schülerinnen (w) und 1 Lehrkraft (l) diese Preise gewinnen?

2007-11-16
- Binome
lassen sich auch mit dem Taschenrechner und mit der Tabellenkalkulation
berechnen.
Taschenrechner: Taste nCr
Tabellenkalkulation:
Befehl KOMBINATIONEN(n;k) - In
der nächsten Stunde werden wir eine Simulation zur Binomialverteilung
durchführen.
Dazu haben wir zwei Befehle der
Tabellenkalkulation wiederholt:
ZUFALLSBEREICH(a;b)
ergibt eine vom Zufallszahlengenerator ausgewählte ganze Zahl zwischen
a und b (jeweils einschließlich). Neue Zufallszahl mit Strg+Shift+F9.
ZUFALLSZAHL(
) ergibt eine vom Zufallszahlengenerator ausgewählte Zahl zwischen 0
(einschließlich) und 1 (ausschließlich). Neue Zufallszahl mit F9
2007-11-21
- Vorgänge
in unserer Umwelt lassen sich häufig durch Simulationen untersuchen
(Wetter, Meeresströmungen, Autoverkehr, Einkaufsverhalten usw.).
- Bedingung
für eine sinnvolle Simulation ist eine gutdurchdachte Modellierung des
zu untersuchenden Gegenstandes.
- Beispielaufgabe:
Mannschaft
A gewinnt beim Tauziehen in 60% aller Wettbewerbe gegen Mannschaft B.
5 Spiele
werden gespielt. Die Mannschaft, die dabei mindestens 3 Siege erreicht
hat hat insgesamt gesiegt.
Frage: Mit welcher
Wahrscheinlichkeit gewinnt Mannschaft A das gesamte Spiel?
Modellierung:- Der
Ausgang eines Spieles wird durch den Aufruf des Zufallszahlengenerators
festgelegt, bei dem eine Dezimalzahl zwischen 0 (einschließlich) und 1
(ausschließlich) "gewürfelt" wird.
- Liegt die
Zufallszahl
zwischen 0 (einschließlich) und 0,6 (ausschließlich), so hat Mannschaft
A ein Teilspiel gewonnen, sonst Mannschaft B.
- Hat
Mannschaft A gewonnen, wird das durch die Zahl 1 dokumentiert, hat B
gewonnen, so wird das durch eine 0 angegeben.
- Über
die Addition dieser Gewinnzahlen kann man die Wahrscheinlichkeit für
den Gesamtgewinn von A experimentell ermitteln.
- Hausaufgabe:
Tabelle in OOo.Calc einrichten und das Ergebnis finden.
2007-11-22
- Die
Besprechung der Hausaufgabe ergab einen Wert von etwa 70% dafür, dass
Mannschaft A das Tauziehen gewinnt (siehe 2007-11-21)
- Die
Frage nach einem "genauen" Wert (wobei damit ein berechneter Wert
gemeint ist) führte uns auf die Formel

Die
Potenzen ergeben sich aus den Pfadregeln für Baumdiagramme. Da es auf
die Reihenfolge der Siege und Niederlagen nicht ankommt, muss noch der
Binom-Faktor hinzugefügt werden.
Das Ergebnis berechnet sich
zu
0,3456 + 0,2592 + 0,07776 = 0,68256. In etwa 68% aller Fälle wird also
Mannschaft A das gesamte Spiel gewinnen. - Allgemein
gilt:
Gibt es bei einem Zufallsversuch nur 2 Ergebnisse,
wobei
das erste Ergebnis mit der Wahrscheinlichkeit p eintritt,
wird
der Zufallsversuch n-mal hintereinander mit Zurücklegen ausgeführt und
tritt
dabei das erste Ereignis k-mal auf,
so berechnet sich die
Wahrscheinlichkeit für diesen Fall zu 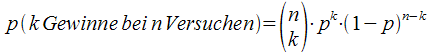
- Unter OOo-Calc wird das
Binom als =Kombinationen(n;k)
eingegeben.
2007-11-23
- Besprechung
der Hausaufgabe: "Chuck Your Luck"
Spielregel: - 3
Würfe mit einem Würfel W6
- Einsatz 1$
- Gewinne:
- 3
mal 6: 6$
- 2 mal 6: 4$
- 1 mal 6:
2$
- Tabelle zur Lösung:


- Der
Erwartungswert ist 1$. Da der Einsatz auch 1$ beträgt, ist das Spiel
fair.
- Da
wir gesehen haben, dass die benutzte Formel auch bei anderen Aufgaben
gut einsetzbar ist, haben wir die Berechnung flexibler gemacht:
Wir
können nun beliebige Werte für n und p wählen:


2007-11-26
- In
dieser Stunde haben wir das Tabellenblatt bei der Lösung mehrerer
Aufgaben aus dem Buch benutzt.
Für
diejenigen, die kein Notebook gehabt haben oder die bei der Tabelle
Schwierigkeiten hatten, hier zum Download die OOo-Calc-Datei Binomialverteilung.ods
2007-11-28
- Wir
haben noch einmal genau die Schreibweise für die Binomialverteilung
betrachtet:
 mit q=1-p.
mit q=1-p. - Da
häufig mehrere Werte der Binomialverteilung addiert werden müssen, ist
es günstig, in der Tabelle (siehe oben) eine Spalte einzufügen, in der
jeweils bis zu einem bestimmten k alle Werte B summiert sind.
Hausaufgabe:
Einfügen einer solchen Spalte in Eure Tabelle.
2007-11-29
- In
den nächsten Stunden werden wir uns damit beschäftigen, wie man mit
Hilfe der Binomialverteilung Tests durchführen kann.
- Das
Schema eines solchen Tests kann folgendermaßen aussehen (Beispiel: Ist
eine 1-Euro-Münze durch die Prägung gezinkt, d. h. sind die
Wahrscheinlichkeiten für die beiden Seiten der Münze verschieden?):
- Hypothese:
Die 1-Euro-Münze ist gezinkt.
- Nullhypothese
oder Normalfall-Hypothese: Die 1-Euro-Münze ist nicht gezinkt und für
die Wahrscheinlichkeiten für Wappen und Zahl gilt:

- Man legt fest, wie oft
ein Zufallsversuch zur Überprüfung der Nullhypothese durchgeführt
werden soll (in unserem Fall 10-mal).
- Man
legt die Größe des Ablehnungsbereiches fest, d. h. man legt fest, bei
welchen Zufallsergebnissen man die Nullhypothese ablehnen wird.
Üblich
sind Bereiche von 1%, 5% oder 10% aller möglichen Ergebnisse (wir haben
5% gewählt). - Da
in unserem Fall sowohl Wappen als auch Zahl ungewöhnlich häufig
vorkommen können, teilen wir den Bereich (5%) in zwei gleich große
Teilbereiche (je 2,5%) auf.
- Wir berechnen die
Binomialverteilung (k ist die Anzahl der Wappen-Würfe):

- Wir
addieren die Wahrscheinlichkeiten B(n;p;0)+B(n;p;1)+... so weit, dass
der Wert 0,025=2,5% nicht überschritten wird und notieren uns die
k-Werte für den Ablehnungsbereich. Es sind die Werte 0 und 1.
- Wir
addieren die Wahrscheinlichkeiten
B(n;p;10)+B(n;p;9)+... so weit, dass der Wert 0,025=2,5% nicht
überschritten wird und notieren uns die k-Werte für den
Ablehnungsbereich. Es sind die Werte 9 und 10.
- Der
Ablehnungsbereich ist die Menge {0;1;9;10}.
- Finden
wir beim Zufallsversuch (10-mal Münze werfen und die Anzahl der Wappen
zählen) ein Ergebnis, das im Ablehnungsbereich vorkommt, können wir mit
5% Fehlerwahrscheinlichkeit die Nullhypothese ablehnen und annehmen,
dass die 1-Euro-Münzen gezinkt sind (bzw. die Münze, die wir untersucht
haben).
- Im Versuch kam 4-mal Wappen und 6-mal Zahl.
Da die 4
nicht im Ablehnungsbereich enthalten ist, können wir die Nullhypothese
nicht ablehnen und müssen annehmen, dass die 1-Euro-Münzen nicht
gezinkt sind.
- Hausaufgabe: Mit den
Ergebnissen des
Würfelversuchs aus dem Unterricht (ungleichmäßiger Würfel mit den
Aufschriften 1; 1; 1; 5; 5; 5 - 50 Würfe) Test durchführen mit der
Hypothese: Der Würfel ist gezinkt.
2007-11-30
- Zwei
wichtige Einsichten gab es in dieser Stunde:
- Da
beim Testen von Hypothesen häufig viele Summanden der Art B(n;p;k)
summiert werden müssen, ist es günstig, eine Tabelle zu benutzen, in
der die Summen von B(n;p;0) bis B(n;p;k) aufgelistet sind. Hier noch
einmal der Link zu eine entsprechenden OOo-Calc-Tabelle.
- Wird
der Stichprobenumfang n größer, so wachsen auch die Mengen des
Annahmebereiches und des Ablehnungsbereiches.
Dabei wächst
die Menge des Annahmebereiches weniger stark an als die Menge des
Ablehnungsbereiches.
Das
bedeutet, dass die Ergebnisse des Tests um so genauer der Wirklichkeit
entsprechen, je größer der Stichprobenumfang ist. - Bei
sehr geringer Stichprobenzahl (n=5; p=0,5) war der Ablehnungsbereich
die leere Menge.
Das bedeutet, dass bei zu geringem
Stichprobenumfang ein Test überhaupt nicht sinnvoll durchgeführt werden
kann.
- Wenn
Ihr bei der Bearbeitung der Hausaufgabe die Tabelle mit den Summen
benutzt, solltet Ihr aber auch für einige der Werte für die
Binomialverteilung "per Hand" ausrechnen, also schriftlich und im Kopf.
Nur so erlangt Ihr die für das Verstehen nötige Routine.
2007-12-03
- Die
OOo-Calc-Tabelle
zur Berechnung des Ablehnungsbereiches ist jetzt verbessert worden: Die
Summe wird nun für k von 0 bis n und in einer weiteren Spalte für k von
n bis 0 aufgelistet.
Die Grenzen des Ablehnungsbereiches
lassen sich so für kleine k und für große k auf gleiche Weise finden. - Bitte
nehmt die Hausaufgaben ernst! Nur wenn ihr die Aufgaben selbstständig
gelöst habt, habt ihr während der Klassenarbeit die notwendige Routine
um eine gute Note schreiben zu können.
Denkt
daran: Nicht Geiz (bei der Lernbereitschaft), sondern Erfolg ist geil.
Und den Erfolg gibt es nur, wenn ihr die dafür notwendigen Aufgaben
erledigt und im Unterricht bei der Sache seid.
2007-12-05
- Da
die Hausaufgabe noch nicht von der Mehrheit geleistet wurde, bleiben
die Aufgaben bestehen.
Bei
einigen von Euch sehe ich schon ein tieferes Verständnis für die Idee
beim Testen mit der Bernoulliverteilung. Schön! Ich hoffe, die anderen
schaffen es bald auch. - Für
die Arbeit gilt: Wir schreiben ohne die Computer, aber Ihr erhaltet
ausgedruckte Tabellen und müsst einzelne Calc-Formeln entwickeln können.
Also:
Die vorhandene Tabelle immer wieder zwischendurch analysieren (=Formeln
durcharbeiten) und mit der Tabelle Aufgaben lösen. - Erläuterungen
zur Anwendung der Binomial-Verteilung, erstellt von einem Schüler.
2007-12-06
- Weitere
Übungen zum Testen mit der Binomial-Verteilung:
Hütchenspiel
- n=10 - p=1/3
Hypothese: Ein "Hellseher" kann
vorhersagen, unter welchem Hütchen der Ball liegt.
Nullhypothese:
Der "Hellseher" kann nicht hellsehen, er rät mit der Wahrscheinlichkeit
1/3.
2007-12-07
- Wir
haben uns über Fehler 1. und 2. Art beim Testen Gedanken gemacht:
- Getestet
werden soll z.B. eine Münze, von der behauptet wird, sie sei durch die
Prägung unsymmetrisch geworden und deshalb sei die Wahrscheinlichkeit
für Wappen (W) und Zahl (Z) nicht jeweils 0,5. Also Hypothese H = p(W)
< > 0,5 . Als Nullhypothese (=Normalfallhypothese) wählt
man N = p(W) = 0,5.
- Zunächst bestimmt man den
Ablehnungsbereich für die Nulhypothese N.
- Nun kann
es beim Testen zwei Ergebnisse geben:
- Das
Ergebnis liegt im Ablehnungsbereich und die Nullhypothese wird abgelehnt,
d.h. man geht davon aus, dass p(W) < > 0,5.
Gilt die Nullhypothese aber
in Wirklichkeit, hat man einen Fehler begangen, den man Fehler 1. Art nennt.
Einen
Fehler 1. Art begeht man mit der Wahrscheinlichkeit α, der
Ablehnungswahrscheinlichkeit der Nullhypothese. - Das
Ergebnis liegt im Annahmebereich und die Nullhypothese wird nicht verworfen,
d.h. man geht davon aus, dass p(W) = 0,5.
Gilt aber in
Wirklichkeit die
Hypothese und man
verwirft die Hypothese, so macht man einen Fehler 2. Art.
Einen
Fehler 2. Art begeht man mit der Wahrscheinlichkeit β.
- Da
man die Wahrscheinlichkeit für die unsymmetrische Prägung des
Geldstückes nicht kennt, kann man den Fehler 2. Art nicht berechnen.
Nimmt man aber einmal an, dass die p(W) = 0,7 gilt, so berechnet sich der Fehler 2. Art folgendermaßen:- Man berechnet die Werte des Annahmebereiches der Nullhypothese.
- Diese Werte bilden den Ablehnungsbereich der Hypothese.
- Es wird die Wahrscheinlichkeit berechnet, dass mit p(W) = 0,7 diese Werte angenommen werden.
- Diese berechnete Wahrscheinlichkeit gibt die Wahrscheinlichkeit für den Fehler 2. Art an.
- Für n=10 und 5% Ablehnungswahrscheinlichkeit ergeben sich folgende Diagramme:
Nullhypothese: Annahmebereich rot, Ablehnungsbereich grün 
Hypothese: Ablehnungsbereich der Hypothese (grün) ist der Annahmebereich der Nullhypothese 
- Wir sehen: Der Fehler 2. Art kann sehr groß werden. Hier tritt ein Fehler 2. Art etwa mit 85% Wahrscheinlichkeit auf.
- Den Fehler 2. Art kann man nur kleiner machen, indem man den Fehler 1. Art vergrößert.
- Beide Fehler lassen sich verkleinern, wenn der Stichprobenumfang erhöht wird.
- Aufgaben zum Weiterdenken:
- Experimentiert mit der OOo-Calc-Tabelle und überprüft die letzten Aussagen experimentell!
- Im
Film über den Test der Wünschelrutengänger und Wasser-Energetisierer
wurde mit n=50 gearbeitet. Wie groß ist hier bei α=5% der Fehler
2. Art, wenn man annimmt, dass die Wahrscheinlichkeit für einen Erfolg
bei 0,9 liegt? Ergebnisse und Informationen dazu von "Quarks & Co" - Übersinnliche Phänomene im Test.
- Warum nimmt man für Tests die Mühen eines Doppelblindversuches auf sich?
- Ein
zweiter Unterrichtsgegenstand entstand in der Stunde aus der
Überlegung, dass bei sehr großer Stichprobenzahl auch extreme
Ergebnisse auftreten können.
- Knacken des Lotto-Jackpots mit 6 Richtigen plus Superzahl
- Auftreten
"ungewöhnlicher" und "unglaublicher" Ziffernfolgen bei Zufallszahlen,
z.B. 3 3 3 3 3 3 3 3 oder 1 2 3 4 5 6 7 8 9 0 usw.
- Sehr viele Geburtstagsdaten sind in den Nachkommastellen der Zahl Pi enthalten. Siehe auch hier.
Die
Ziffern der Nachkommastellen von Pi folgen (wahrscheinlich) vollkommen
zufällig aufeinander. Es kann keine Formel angegeben werden, die der
Reihe nach die Nachkommastellen angibt. - Bewiesen(!) ist, dass in jeder unendlichen Aufeinanderfolge vollkommen zufälliger Ziffern jede beliebig lange vorgegebene Ziffernfolge auftaucht.
Codiert
man Buchstaben durch Zahlen, so kann man auch sagen: Jeder vorgegebene
Text taucht in der benutzten Codierung in dieser unendlichen Folge auf.
Das
kann ein einfacher Satz wie dieser gerade gelesene Satz sein, es kann
aber auch ein ganzes Buch und auch eine ganze Bibliothek sein.
Der 27. Harry-Potter-Band - wenn er denn je geschrieben würde - existiert schon jetzt codiert in jeder unendlichen Aufeinanderfolge vollkommen zufälliger Ziffern.
Und nicht nur das: Sogar seine Übersetzungen
in jede existierende und ausgedachte Sprache existieren ebenfalls
schon. Man muss die Stelle in der unendlichen Folge nur finden ;-)
Und
weiter: Selbst wenn ein einziger Buchstabe in einem solchen virtuellen
Band geändert würde, auch dazu existiert schon der gesamte Band mit
dieser Änderung in jeder ... - Leider
haben wir nicht unendlich viel Zeit, um eine einzige solcher
Folgen zu untersuchen. Was gäbe es da alles zu entdecken!
2007-12-10
- Wir haben uns noch einmal überlegt, was es mit dem Fehler 1. Art und dem Fehler 2. Art auf sich hat.
In Kürze:- Wenn man die Nullhypothese ablehnt, obwohl sie richtig ist, begeht man einen Fehler 1. Art, genannt α.
- Wenn
man die Nullhypothese annimmt (oder anders gesagt: wenn man die
Hypothese ablehnt), obwohl die Hypothese stimmt, dann begeht man einen
Fehler 2. Art, genannt β.
- Den Wert für β
bestimmt man, indem man für bei der Verteilung für die Hypothese die
Wahrscheinlichkeiten für die Ergebnisse summiert, die im Annahmebereich
der Nullhypothese liegen.
- α und β hängen voneinander ab: je größer α, desto kleiner β, je kleiner α, desto größer β.
- α und β können beide nur dann verkleinert werden, wenn der Stichprobenumfang n zunimmt.
- Ausführliche Betrachtung zum Fehler 1. und 2. Art.
Das Dokument ist ein Script der Uni Bielefeld, aber durchaus für Euch
in den meisten Abschnitten zu verstehen. Die anderen Abschnitte sind
etwas für die, die weiterdenken wollen.
- Hausaufgabe: Seite 99 Aufgabe 8
2007-12-12
- Besprechung der Hausaufgabe, Wiederholung der Benutzungsregeln für die OOo-Calc-Tabelle.
2007-12-13
- Neben einigen Wiederholungen haben wir heute den "Vorzeichentest" neu besprochen.
Man benutzt ihn, wenn es bei einem Test nur darauf ankommt, ob eine Messgröße einer Bedingung entspricht oder nicht.
Beispiele:
"Ist ein neues Medikament besser als ein altes?" "Kann man in einem
geheizten Zimmer besser schlafen als in einem kalten?" "Können Frauem
besser Auto fahren als Männer?"
Als Ergebnis schreibt man sich immer
nur ein + (Bedingung ist erfüllt) oder ein - (Bedingung ist
nicht erfüllt) und testet dann die Anzahl der +Zeichen darauf, ob
die Nullhypothese (=es gibt gleiche viele + und -, d.h. p(+) = p(-) =
0,5) angenommen ode abgelehnt wird. - Wir haben den
Zufallsversuch "Schüler(in) A ist ein(e) bessere(r)
Stein-Schere-Papier-Spieler(in) als Schüler(in) B" durchgeführt und
getestet, ob die Nullhypothese (=beide Spieler(innen) sind gleich gut)
verworfen werden kann oder nicht.
Festgelegt war vorher α=0,05.
In
einer von 12 Zweier-Gruppen lag das Ergebnis im Ablehnungsbereich, d.h.
wir haben geschlossen: Frauke war besser als Christiane.
Allerdings
beträgt die Irrtumswahrscheinlichkeit 5%. 5% von 12 ist 0,6, gerundet
1. Das heißt: Es ist zu erwarten, dass bei einem von 12 Versuchen 1
Ergebnis im Ablehnungsbereich liegt, obwohl die Nullhypothese stimmt.
Genau das hat sich in unserem Klassenversuch ergeben. Ist nun Frauke
doch nicht besser als Christiane?
2007-12-14
- Wiederholung zur Klassenarbeit
- Themen der Klassenarbeit:
- Berechnung der Anzahl der Möglichkeiten bei einem Zufallsversuch
- Definition und Rechenregeln für Binome der Art

- Berechnung von Wahrscheinlichkeiten mit Binomen, z.B.
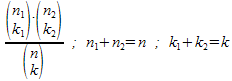
- Bernoulli-Formel:

- Test mit Bernoulli-Ketten (= n Versuche, jedesmal 2 mögliche Ergebnisse, alle Versuche unabhängig voneinander)
Hypothese H, Normalfallhypothese N, Ablehnungsbereich, Annahmebereich, einseitig, zweiseitig, Irrtumswahrscheinlichkeit - Fehler 1. und 2. Art
- Vorzeichentest
2007-12-17
- Wiederholung zur Klassenarbeit
- Da
es Euch immer noch Schwierigkeiten bereitet, bei Tests zwischen dem
Fehler 1. und 2. Art zu unterscheiden, hier noch eine Übersicht:
- Fehler
1. Art: Im Zufallsversuch erhält man ein Ergebnis aus dem
Ablehnungsbereich. Man lehnt die Nullhypothese ab, obwohl sie in
Wirklichkeit wahr ist.
- Fehler 2. Art: Im Zufallsversuch erhält
man ein Ergebnis aus dem Annahmebereich. Man lehnt die Nullhypothese
nicht ab, obwohl sie in Wirklichkeit falsch ist.
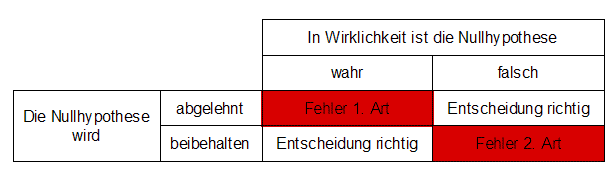
- Der Ablehnungsbereich der Hypothese ist identisch mit dem Annahmebereich der Nullhypothese.
- Da einige keinen Taschenrechner mit nCr-Taste haben, werdet Ihr in der Klassenarbeit ein Blatt mit einer Tabelle zur Bestimmung von Binomen bekommen.
Mit dem Link könnt Ihr Euch die OOo-Calc-Tabelle herunterladen und ausprobieren.
2007-12-19
weiter mit Inhaltsmessung



 , nennt die rechts stehende Klammer "Binom"
(von bi = zwei und nomos = der Name) und spricht es "27 über 12" aus.
, nennt die rechts stehende Klammer "Binom"
(von bi = zwei und nomos = der Name) und spricht es "27 über 12" aus. 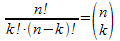 Möglichkeiten. Aussprache: "n über k"
Möglichkeiten. Aussprache: "n über k" Möglichkeiten.
Möglichkeiten. Möglichkeiten.
Möglichkeiten. Möglichkeiten, verschiedene Ergebnisse zu
erhalten.
Möglichkeiten, verschiedene Ergebnisse zu
erhalten.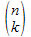 Möglichkeiten für unterschiedliche Ergebnisse.
Möglichkeiten für unterschiedliche Ergebnisse.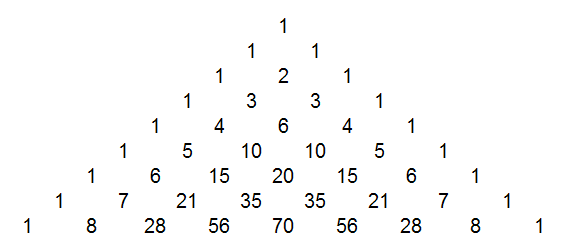
 entstehen:
entstehen: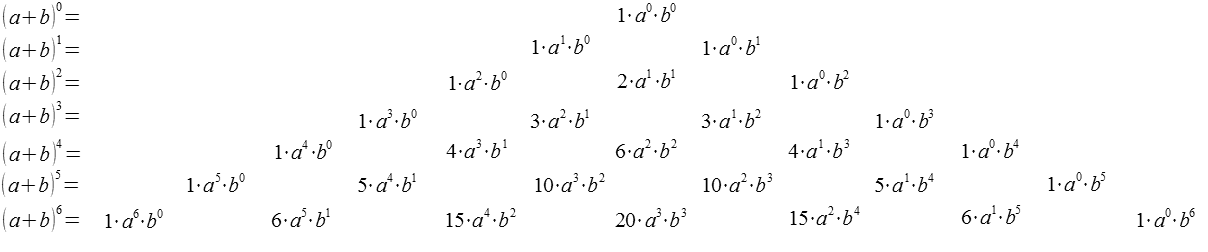

 für n>0 und k<=n ist nach dem
Pascalschen-Binom-Dreieck auch noch sinnvoll zu definieren
für n>0 und k<=n ist nach dem
Pascalschen-Binom-Dreieck auch noch sinnvoll zu definieren  , wobei man auf den Wert 0!=1 durch
folgende Überlegung kommt:
, wobei man auf den Wert 0!=1 durch
folgende Überlegung kommt:
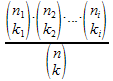


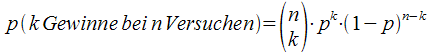




 mit q=1-p.
mit q=1-p.