Überholvorgang

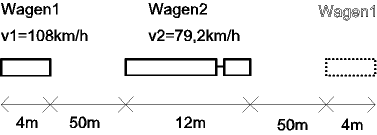
Ein PKW (Wagen 1, Länge 4m) fährt mit 108km/h im Abstand 50m hinter einem Lastwagen (Wagen 2, Länge 12m), dessen Geschwindigkeit 79,2km/h beträgt.
Die (nicht maßstabsgerechte) Abbildung oben zeigt diese Ausgangssituation.

Wieviel freier Raum muss auf der Gegenfahrbahn sein, damit ein Überholen gefahrlos möglich ist? Der PKW soll erst dann einscheren, wenn der Sicherheitsabstand von 50m wieder erreicht ist.

1. Lösungsschritt: Umrechnungen und Vorüberlegungen
v1=108km/h=30m/s
v2=79,2km/h=22m/s
Die Vorderfront des PKWs muss zurücklegen: 50m Abstand, 12m Länge des LKWs, 50m Abstand, 4m Länge des PKWs, also zusammen 116m.

2. Lösungsschritt: Rechnung im Bezugssystem des Lastwagens
In diesem Fall beträgt die "wirksame" Geschwindigkeit des PKWs 30m/s-22m/s=8m/s.
Wegen v=s/t gilt t=s/v.
Der PKW benötigt also für den Überholvorgang t=116m/8(m/s)=14,5s. Die dabei auf der Straße zurückgelegte Strecke errechnet sich aus dieser Zeit und der Geschwindigkeit v₁: s=v₁*t=30m/s*14,5s=435m.
Falls ein entgegenkommender Wagen auch mit 108km/h fahren sollte, muss die freie Strecke doppelt so lang sein, also 2*435m=870m.

3. Lösungsschritt: Rechnung im Bezugssystem der Straße
Zunächst werden die Bewegungsgleichungen für den PKW und den LKW in der Form s=v*t+s₀ aufgestellt. Dabei soll für den PKW gelten: s₀=0m.
PKW: s₁=30m/s*t₁
LKW: s₂=22m/s*t₂+62m
Die 62m setzen sich zusammen aus 50m Abstand und 12m LKW-Länge.
Der PKW darf nach dem Überholen wieder einscheren, wenn er 54m vor dem LKW ist (50m Abstand plus 4m PKW-Länge). Es muss also gelten: s₁=s₂+54m und t₁=t₂.
Daraus folgt: 30m/s*t=22m/s*t+62m+54m, also 8m/s*t=116m, also t=116/8s=14,5s.
Weitere Rechnung wie unter Schritt 2.