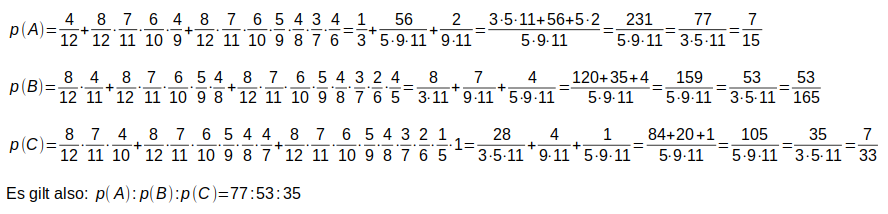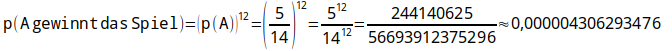Historische Aufgaben und
Lösungen zur Stochastik mit Simulationen
1. Das Problem des Chevalier de Meré
Blaise Pascal und Pierre de Fermat beschäftigten sich mit folgendem
Problem, auf das sie Chevalier de Meré hingewiesen hat:
Worauf sollte man lieber wetten,
auf mindestens eine 6 beim 4-fachen Würfeln mit einem Würfel W6 oder
auf mindestens einen 6-er-Pasch (2 Sechsen) beim 24-fachen Würfeln mit 2
Würfeln W6?
Berechnung der Wahrscheinlichkeiten:

Mindestens eine 6 beim 4-maligen Würfeln ist also etwas wahrscheinlicher als
mindestens ein 6-Pasch beim 24-maligen Würfeln.
Bei 51,77% aller Versuche (mindestens eine 6 beim 4-maligen Würfeln) gewinnt
man also eher, als dass man verliert.
Simulation (Java-Programm)
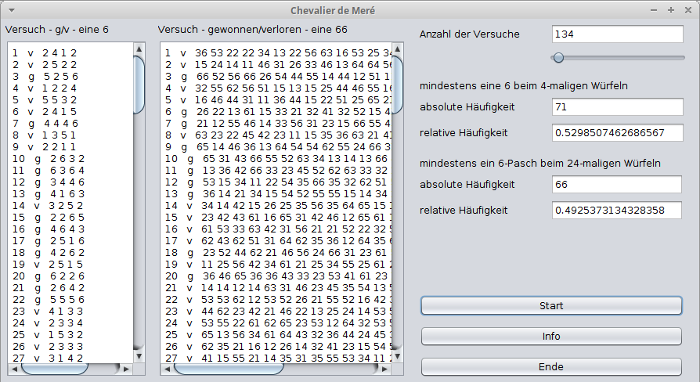
Das Programm führt die beiden Versuche maximal 10000-mal durch und gibt für
jeden Versuch die absolute und relative Häufigkeit für einen Gewinn aus.
2. Die Wahrscheinlichkeit von Würfelsummen beim
Würfeln mit mehreren Würfeln.
Bei vielen historischen Aufgaben wird nach der Wahrscheinlichkeit
gefragt, mit der sich eine bestimmte Würfelsumme beim mehrfachen Würfeln
ergibt.
Hier eine kleine Auswahl, die mit den Namen Galilei, Leibniz und
D'Alembert verknüpft sind:
Aufgabe 1:
Beim Würfeln mit 2 Würfeln W6 ergeben sich die Summen 11 und 12 aus den
Würfelzahlen 5+6=11 und 6+6=12.
Die Summe 7 ergibt sich dagegen aus den 3 Kombinationen 1+6=2+5=3+4=7
Man könnte daraus schließen, dass die Wahrscheinlichkeiten für die Summe
11 und die Summe 12 gleich sind (jeweils eine Ziffernkombination) und dass
die Summe 7 dreimal so häufig vorkommt.
Warum ist diese Vermutung falsch?
Aufgabe 2:
Würfelt man mit 3 Würfeln W6, so ergibt sich die Augensumme 11 aus den 6
Kombinationen 1+4+6, 1+5+5, 2+3+6, 2+4+5, 3+3+5, 3+4+4.
Die Augensumme 12 ergibt sich ebenfalls aus 6 Kombinationen: 1+5+6, 2+4+6,
2+5+5, 3+3+6, 3+4+5, 4+4+4.
Sind die beiden Augensummen deshalb gleich wahrscheinlich?
Aufgabe 3:
Wie Aufgabe 2, nur mit den Würfelsummen 9 und 10:
9=1+2+6=1+3+5=1+4+4=2+2+5=2+3+4=3+3+3
10=1+3+6=1+4+5=2+2+6=2+3+5=2+4+4=3+3+4
Lösung:
Aufgabe1:
Jeder Würfel kann 6 verschiedene Zahlen zeigen, es gibt also 6∙6=36
verschiedene Ergebnisse.
Für die Summe 12 müssen beide Würfel die 6 zeigen. Also nur eines der 36
verschiedenen Ergebnisse ist richtig.
Für die Summe 11 muss entweder der Würfel A die 5 und der Würfel B die 6
zeigen oder aber der Würfel A die 6 und der Würfel B die 5.
Es sind also 2 der 36 verschiedenen Ergebnisse ist richtig.
Für die Summe 7 muss man entsprechend die folgenden Ergebnisse
berücksichtigen. Vor dem Pluszeichen steht das Ergebnis des Würfels A und
hinter dem Pluszeichen das Ergebnis des Würfels B:
1+6 = 6+1 = 2+5 = 5+2 = 3+4 = 4+3 = 7
Es gibt also 6 verschiedene Würfelergebnisse, die zur Augensumme 7 führen.
Damit ergeben sich folgende Wahrscheinlichkeiten:
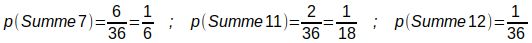
Die Augensumme 11 sollte also doppelt so oft vorkommen wie die Augensumme
12.
Die Augensumme 7 sollte 6-mal so häufig vorkommen wie die Augensumme 12.
Aufgabe 2:
Die Lösung ergibt sich analog zu Aufgabe 1.
Sind alle 3 Würfelzahlen gleich, so wird das Ergebnis (z. B. 4+4+4 = 12)
nur einmal berücksichtigt.
Sind 2 Würfelzahlen gleich, so gibt es 3 zu berücksichtigende Ergebnisse
(z. B. 1+5+5 = 5+1+5 = 5+5+1 = 11).
Sind alle Würfelzahlen verschieden, so gibt es 6 zu berücksichtigende
Ergebnisse (z. B. 1+5+6 = 1+6+5 = 5+1+6 = 5+5+1 = 6+1+5 = 6+5+1 = 12).
Beim dreifachen Wurf gibt es 6∙6∙6=216 verschiedene Ergebnisse.
Die Augensumme 11 ergibt sich also in (siehe oben) 6+3+6+6+3+3=27 von 216
Fällen.
Die Augensumme 12 ergibt sich also in (siehe oben) 6+6+3+3+6+1=25 von 216
Fällen.
Damit ergeben sich folgende Wahrscheinlichkeiten:

Die Augensumme 11 kommt also häufiger vor als die Augensumme 12.
Aufgabe 3:
Analog zur Aufgabe 2 ergibt sich:
Die Augensumme 9 ergibt sich also in (siehe oben) 6+6+3+3+6+1=25 von 216
Fällen.
Die Augensumme 10 ergibt sich also in (siehe oben) 6+6+3+6+3+3=27 von 216
Fällen.
Damit ergeben sich folgende Wahrscheinlichkeiten:
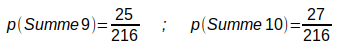
Die Augensumme 10 kommt also häufiger vor als die Augensumme 9.
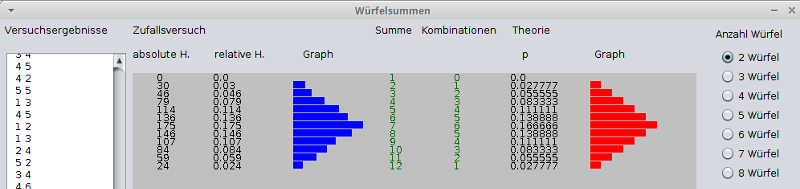
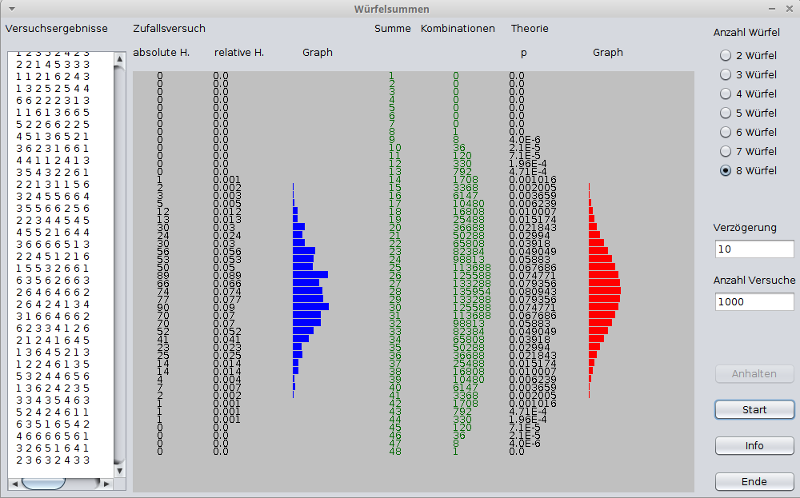
Das Programm Wuerfelsummen.jar
simuliert das Würfeln mit 2 bis 8 Würfeln.
Es werden die Würfelsummen ermittelt und als absolute und relative
Häufigkeit angegeben und zusätzlich graphisch dargestellt.
Auch die theoretisch ermittelten Werte werden als Zahlenwert und als Gaph
angezeigt.
Zwei Screenshots zum Programm:
3. Das Ziegenproblem
In einer Spielshow kann ein Teilnehmer ein Auto
gewinnen. Hinter einer von 3 geschlossenen Türen befindet sich der Preis.
Hinter den beiden anderen Türen stehen Ziegen (daher der Name), die
"Niete" bedeuten.
Der Kandidat wählt zunächst eine Tür. Darauf öffnet der Spielleiter eine
andere Tür, hinter der sich eine Ziege befindet. Darauf darf der Kandidat
seine Auswahl noch einmal ändern. Wird durch das Ändern der Auswahl die
Chance für einen Gewinn verbessert oder verschlechtert oder bleibt die
Gewinnchance gleich?
Dieses Problem wurde in den letzten Jahrzehnten teils heftig diskutiert
(siehe z. B. Wikipedia-Artikel).
Lösung:
Bei der ersten Wahl des Kandidaten besteht die Wahrscheinlichkeit 1/3 für
einen Gewinn, weil bei 1 Auto und 2 Ziegen hinter drei Türen die
Gewinnwahrscheinlichkeit für jede Tür gleich ist.
Die Wahrscheinlichkeit, dass sich das Auto hinter den beiden nicht
gewählten Türen befindet, ist also 2/3.
Da der Spielleiter eine dieser beiden Türen öffnet und zeigt, dass sich
hinter der Tür eine Ziege befindet, gilt die Gewinnwahrscheinlichkeit von
2/3 also nun allein für die verbleibende Tür.
Es ist also sinnvoll, die Auswahl zu ändern und die bisher nicht gewählte
verschlossene Tür zu wählen.
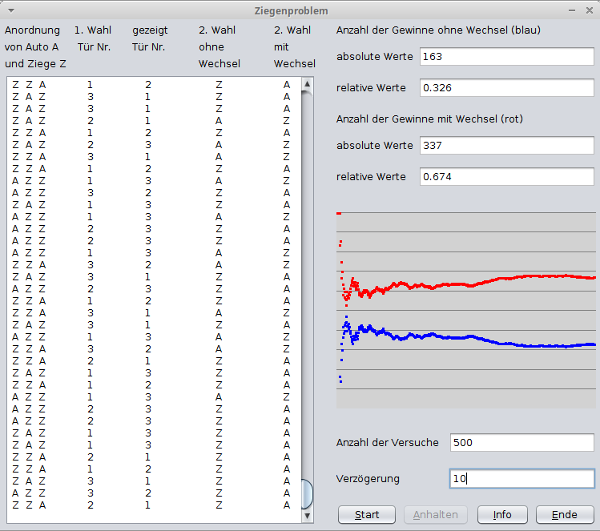
Das Programm Ziegenproblem.jar führt
Simulationen durch, die das Gewinnspiel nachahmen.
Angezeigt werden jeweils (von links nach rechts) die Anordnung des
Autos(A) und der Ziegen(Z) hinter den Türen,
die Wahl (Nummer der Tür) des Kandidaten,
die Nummer der durch den Spielleiter geöffneten Tür
und das Ergebnis für 'kein Wechsel' bzw. 'mit Wechsel'.
Im rechten Bereich wird die Auswertung in absoluten und relativen Werten
angezeigt und durch zwei Graphen veranschaulicht.
Als Startbedingungen können die Anzahl der Versuche und die Verzögerung
(=Zeit zwischen 2 Versuchen in ms) eingegeben werden.
Screenshot des Programms:
4. Problem 1 aus "Tractatus de ratiociniis in
aleae ludo" von Christian Huygens.
Zwei Spieler A und B würfeln mit zwei Würfeln.
Spieler A gewinnt, wenn er die Würfelsumme 6 wirft, Spieler B gewinnt bei
der Würfelsumme 7.
Spieler A fängt an und würfelt einmal. Falls er nicht gewinnt, hat Spieler
B 2-mal die Möglichkeit bei seinem Wurf zu gewinnen.
Danach würfelt Spieler A 2-mal. Das Spiel endet, wenn ein Spieler seine
Würfelsumme erreicht hat.
Reihenfolge der Spieler beim Würfeln: A B B A A B B A A ... Bis auf den
Anfang darf also jeder Spieler 2-mal würfeln, bevor der andere Spieler an
der Reihe ist.
Lösung:
Die Gewinn-Würfelsumme 6 für Spieler A kann erreicht werden durch die
Kombinationen 1+5, 2+4, 3+3, 4+2, 5+1, also durch 5 Kombinationen bei 36
Kombinationen insgesamt. Daraus folgt für die Wahrscheinlichkeit: p(A)=5/36.
Die Gewinn-Würfelsumme 7 für Spieler B kann erreicht werden durch die
Kombinationen 1+6, 2+5, 3+4, 4+3, 5+2, 6+1, also durch 6 Kombinationen bei
36 Kombinationen insgesamt. Daraus folgt für die Wahrscheinlichkeit:
p(B)=6/36=1/6.
Für die folgende Rechnung benötigen wir die Summenformel  .
.
Herleitung der Summenformel:

Berechnung der Wahrscheinlichkeit für einen Gewinn von A. Dazu werden alle
Wahrscheinlichkeiten der Gewinn-Ausgänge addiert:


Das Programm simuliert den Vorgang:
Die Anzahl der Spiele und die Verzögerung (Zeit zwischen 2 Spielen) können
gewählt werden.
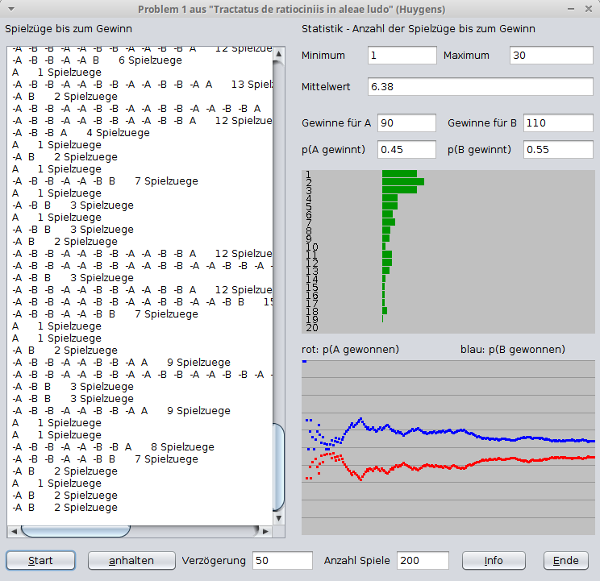
Links wird der Spielverlauf für jedes Spiel angezeigt.
Rechts werden die minimale und die maximale Anzahl der notwendigen Spielzüge
bis zu einem Gewinn angegeben.
Auch die durchschnittliche Anzahl der Spielzüge wird berechnet.
Die obere Grafik zeigt, wie häufig Spiele mit n Spielzügen auftreten.
In der unteren Grafik werden die Gewinnwahrscheinlichkeiten für Spieler A
und B einander gegenüber gestellt.
5. Problem 2 aus "Tractatus de ratiociniis in
aleae ludo" von Christian Huygens.
In einer Urne befinden sich 12 Kugeln, die durch
Berührung nicht zu unterscheiden sind. 4 Kugeln sind weiß und 8 Kugeln
sind schwarz gefärbt.
3 Spieler A, B und C ziehen abwechselnd zufällig je eine Kugel, ohne sie
wieder zurück zu legen. Der erste Spieler, der eine weiße Kugel gezogen
hat, gewinnt.
Die Spieler ziehen in alphabetischer Reihenfolge. Wie groß sind die
Wahrscheinlichkeiten für einen Gewinn für jeden der Spieler?
Lösung:
In folgendem reduzierten Baumdiagramm bedeutet Aw, dass A eine weiße Kugel
zieht und As, dass A eine schwarze Kugel zieht. Für B und C gilt das
entsprechend.
Da ohne Zurücklegen gezogen wird, kann der vollständige reduzierte Baum
gezeichnet werden:

Daraus folgen die Wahrscheinlichkeiten für einen Gewinn von A, B und
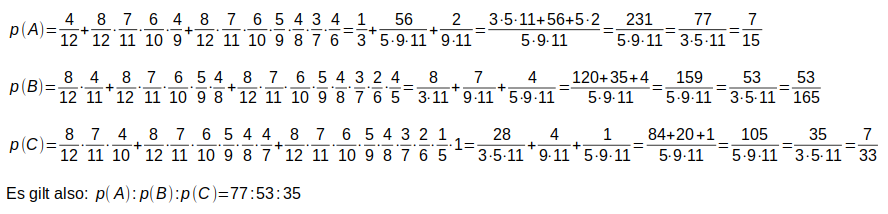
Das Programm simuliert den Vorgang:
Die Anzahl der Spiele und die Verzögerung (Zeit zwischen 2 Spielen) können
gewählt werden.
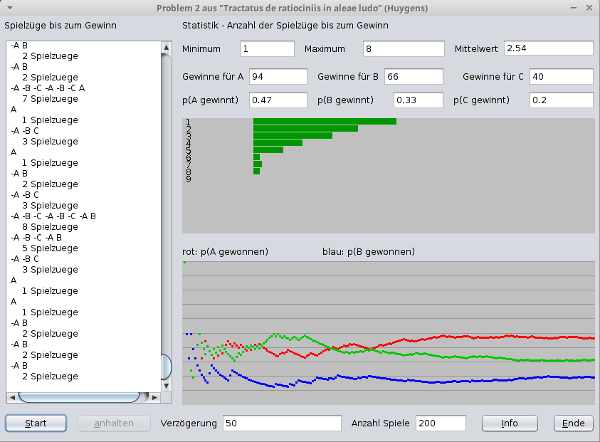
Links wird der Spielverlauf für jedes Spiel angezeigt.
Rechts werden die minimale und die maximale Anzahl der notwendigen Spielzüge
bis zu einem Gewinn angegeben.
Auch die durchschnittliche Anzahl der Spielzüge wird berechnet.
Die obere Grafik zeigt, wie häufig Spiele mit n Spielzügen auftreten.
In der unteren Grafik werden die Gewinnwahrscheinlichkeiten für Spieler A, B
und C einander gegenüber gestellt.
6. Problem 3 aus "Tractatus de ratiociniis in
aleae ludo" von Christian Huygens.
Ein Kartenspiel besteht aus 40 Karten in den
Farben rot, gelb, grün, blau. Zu jeder Farbe gehören 10 Karten, die
jeweils durchnummeriert sind von 1 bis 10.
Spieler A zieht 4 Karten und wettet darauf, dass er von jeder Farbe eine
Karte zieht. Spieler B wettet dagegen.
Wie groß sind die Wahrscheinlichkeiten für einen Gewinn für jeden der
Spieler?
Lösung:
Es ist egal, welche Karte A zu Beginn zieht. Er hat 40 Gewinnkarten von 40
Karten insgesamt: p(1. Karte für Gewinn) = 40/40.
Für die 2. Gewinnkarte stehen nun noch 30 Karten von insgesamt 39 Karten
bereit: p(2. Karte für Gewinn)=30/39.
Für die 3. Gewinnkarte stehen nun noch 20 Karten von insgesamt 38 Karten
bereit: p(3. Karte für Gewinn)=20/38.
Für die 4. Gewinnkarte stehen nun noch 10 Karten von insgesamt 37 Karten
bereit: p(4. Karte für Gewinn)=10/37.
Insgesamt ergeben sich damit folgende Gewinnwahrscheinlichkeiten:

A gewinnt also etwas mehr als 10% aller Spiele.
Das Programm simuliert den Vorgang:
Die Anzahl der Spiele und die Verzögerung (Zeit zwischen 2 Spielen) können
gewählt werden.
Links wird der Spielverlauf für jedes Spiel angezeigt.
Rechts wird angegeben, wie oft in den Spielen n Farben gezogen wurden.
Darunter werden die Anzahl der Gewinne von A und B angezeigt und die dazu
gehörenden Gewinn-Wahrscheinlichkeiten.
Die obere Grafik zeigt die Häufigkeit der Anzahl der verschiedenen Farben.
In der unteren Grafik werden die Gewinnwahrscheinlichkeiten für Spieler A
und B einander gegenüber gestellt.

7. Problem 4 aus "Tractatus de ratiociniis in
aleae ludo" von Christian Huygens.
In einer Urne befinden sich 12 Kugeln, die durch
Berührung nicht zu unterscheiden sind. 4 Kugeln sind weiß und 8 Kugeln
sind schwarz gefärbt.
Spieler A wettet mit Spieler B, dass er beim Ziehen von 7 Kugeln ohne
Zurücklegen genau 3 schwarze Kugeln erhält.
Gefragt ist die Wahrscheinlichkeit, mit der dieses Ereignis eintritt.
Lösung:
Anmerkung: Wenn 3 von 7 Kugeln schwarz sind, sind die anderen Kugeln weiß.
Es werden also alle vorhandenen weißen Kugeln gezogen.
Exkus: Anzahl der möglichen Ergebnisse beim Ziehen ohne Zurücklgen.
Am Beispiel: Von n=12 Kugeln werden k=7 Kugeln gezogen. Bei der ersten Kugel
hat man 12 Möglichkeiten, bei der 2. Kugel noch 11 Möglichkeiten usw.,
insgesamt sind es 12∙11∙10∙9∙8∙7∙6 Möglichkeiten.
Da es auf die Reihenfolge aber nicht ankommt, muss man das Ergebnis durch
die Anzahl der Möglichkeiten dividieren, auf die man die 7 Kugeln anordnen
kann: Für die erste Ergebnis-Kugel hat man 7 Plätze, für die nächste nur
noch 6 Plätze usw., insgesamt sind es also 7∙6∙5∙4∙3∙2∙1 Plätze.
Mit der Abkürzung n!=1∙2∙3∙...∙n kann man schreiben: 7∙6∙5∙4∙3∙2∙1=7! und
12∙11∙10∙9∙8∙7∙6=12∙11∙10∙9∙8∙7∙6∙5∙4∙3∙2∙1/(5∙4∙3∙2∙1)=12!/5!
Um 12! schreiben zu können, musste also mit (12-7)!=5! erweitern.

Die Abkürzung ganz rechts nennt man Binom.

Im Programm können die Anzahl der Spiele
und die Verzögerung (Zeit zwischen 2 Spielen) gewählt werden.
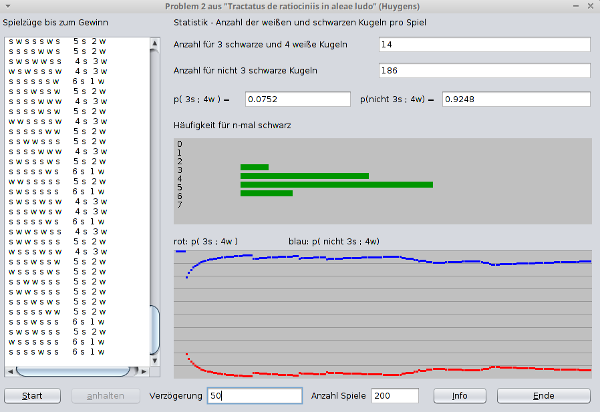
Links wird für jedes Spiel die Farbe der gezogenen Kugel angezeigt.
Rechts wird angegeben, wie viele der Spiele gewonnen und wie viele verloren
wurden.
Darunter stehen die relativen Häufigkeiten für Gewinn und Verlust.
Die obere Grafik zeigt, wie häufig Spiele mit genau n (0 bis 7) schwarzen
Kugeln auftreten.
In der unteren Grafik werden die Gewinnwahrscheinlichkeiten für Spieler A
und B\n einander gegenüber gestellt.
8. Problem 5 aus "Tractatus de ratiociniis in
aleae ludo" von Christian Huygens.
Zwei Spieler A und B besitzen zu Beginn eines
Spieles jeweils 12 Münzen. Sie spielen mit 3 Würfeln.
Wenn die Würfelsumme 11 ist, gibt A eine Münze an B.
Wenn die Würfelsumme 14 ist, gibt B eine Münze an A.
Derjenige, der zuerst alle Münzen besitzt, gewinnt das Spiel.
Zu zeigen ist, dass sich die Gewinnchancen von A zu B wie 244.140.625 zu
282.429.536.481 verhalten.
Lösung:
Die Würfelsumme 11 ergibt sich bei folgenden 27 Würfelergebnissen:
1-4-6 ; 1-5-5 ; 1-6-4 ; 2-3-6 ; 2-4-5 ; 2-5-4 ; 2-6-3 ; 3-2-6 ; 3-3-5 ;
3-4-4 ; 3-5-3 ; 3-6-2 ; 4-1-6 ; 4-2-5 ; 4-3-4 ; 4-4-3 ; 4-5-2 ; 4-6-1 ;
5-1-5 ; 5-2-4 ; 5-3-3 ; 5-4-2 ; 5-5-1 ; 6-1-4 ; 6-2-3 ; 6-3-2 ; 6-4-1
Die Würfelsumme 14 ergibt sich bei folgenden 15 Würfelergebnissen:
2-6-6 ; 3-5-6 ; 3-6-5 ; 4-4-6 ; 4-5-5 ; 4-6-4 ; 5-3-6 ; 5-4-5 ; 5-5-4 ;
5-6-3 ; 6-2-6 ; 6-3-5 ; 6-4-4 ; 6-5-3 ; 6-6-2
Da es bei 3 Würfeln insgesamt 6∙6∙6=216 verschiedene Ergebnisse gibt,
betragen die Wahrscheinlichkeiten für die Würfelsummen 11 und 14

Ergibt sich beim Würfeln eine andere Summe als 11 oder 14, ändert sich am
Spielstand nichts und es wird noch einmal gewürfelt.
Insgesamt gibt es also nur 9+5=14 Fälle, in denen eine Münze den Besitzer
wechselt und es gelten für A und B die Gewinnwahrscheinlichkeiten

Theoretisch könnte ein Spiel unendlich lange dauern, wenn z. B. immer
abwechselnd A und B eine Münze bezahlen müssen. Glücklicherweise muss man
aber nicht alle möglichen Spielzüge bei der Berechnung berücksichtigen, wenn
man Folgendes beachtet:
Ist ein bestimmter Spielstand erreicht, kommt es nicht auf die Vorgeschichte
an, da die Wahrscheinlichkeit für einen Gewinn davon unabhängig ist.
Beispiel: Mit der Wahrscheinlichkeit p(A) ergibt sich zu Beginn der
Spielstand "A hat 13 Münzen und B hat 11 Münzen". Nun kann das Spiel
beliebig weiter gehen. Falls sich dann wieder der Spielstand "A hat 13
Münzen und B hat 11 Münzen"ergibt, ist es so, als wenn die dazwischen
liegenden Spielzüge nicht erfolgt wären.
Da A 12-mal eine Münze von B bekommen muss, um zu gewinnen, ist die
Gewinnwahrscheinlichkeit für das ganze Spiel für A
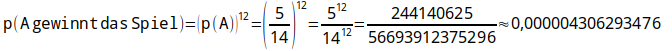
und entsprechend für B

Daraus folgt: p(A gewinnt das Spiel) : p(B gewinnt das Spiel) = 512
: 912 = 244140625 : 282429536481.
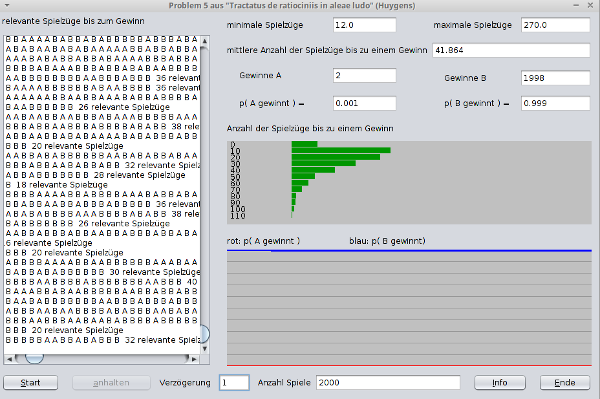
Im Programm können die Anzahl der Spiele
und die Verzögerung (Zeit zwischen 2 Spielen) gewählt werden.
Links wird für jedes Spiel die Reihenfolge der Münzgewinner angezeigt.
Rechts oben werden Statistiken zur minimalen, maximalen und
durchschnittlichen Anzahl der relevanten Spielzüge angegeben.
Darunter stehen die absoluten und relativen Häufigkeiten für Gewinne von A
und B.
Die obere Grafik zeigt, wie viele relevante Spielzüge für den Gewinn eines
Spieles notwendig waren.
In der unteren Grafik werden die Gewinnwahrscheinlichkeiten für Spieler A
und B einander gegenüber gestellt.
Man beachte, dass sich aussagekräftige Ergebnisse erst für eine sehr große
Anzahl von Spielen ergeben.
Weiter bemerkenswert: Es gibt 15 verschiedene Gewinn-Ergebnisse für Spieler
A und 27 für Spieler B.
Man vergleiche die Summe 15+27=42 mit der mittleren Anzahl von relevanten
Spielzügen, bis ein Sieg erfolgt ist.
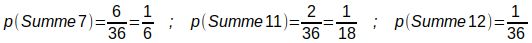



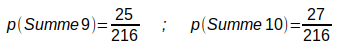



 .
.