Beispiel : (Modrow, S.19 A.2a)
Beschreiben Sie die Steuerung einer Verkehrsampel als endlichen Automaten. Eingabezeichen sind die Signale F (Farbe halten) und W (Farbe wechseln). Ausgabezeichen sind die Farbkombinationen der Ampel: rot (r), rot-gelb (rg), grün (ü) und gelb (g).

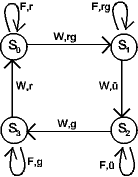
Lösung als Zustandsdiagramm:

Lösung als Zustandstabelle:
 

	F	W
S0	S0,r	S1,rg
S1	S1,rg	S2,ü
S2	S2,ü	S3,g
S3	S3,g	S0,r

Codierung:

4 Zustände: 2-stellige Dualzahl

S0	S1	S2	S3
00	01	10	11

2 verschiedene Eingaben: 1-stellige Dualzahl

F	W
0	1

4 verschiedene Ausgaben: 2-stellige Dualzahl

r	rg	ü	g
00	01	10	11

Schaltwerttabelle:

aktueller Zustand: s₁s₀
Eingabe: e
Folgezustand: S₁S₀
Ausgabe: A₁A₀
 

s1	s0	e	S1	S0	A1	A0
0	0	0	0	0	0	0
0	0	1	0	1	0	1
0	1	0	0	1	0	1
0	1	1	1	0	1	0
1	0	0	1	0	1	0
1	0	1	1	1	1	1
1	1	0	1	1	1	1
1	1	1	0	0	0	0

Schaltfunktionen:

S₁ = (-s₁ ^ s₀ ^ e) v (s₁ ^ -(s₀ ^ e))

S₀ = (-s₀ ^ e) v (s₀ ^ -e)

A₁ = S₁

A₀ = S₀

in der disjunktiven Normalform heißen die Terme:

S₁ = (-s₁ ^ s₀ ^ e) v (s₁ ^ -s₀ ^ -e) v (s₁ ^ -s₀ ^ e) v (s₁ ^ s₀ ^ -e)

S₀ = (-s₁ ^ -s₀ ^ e) v (-s₁ ^ s₀ ^ -e) v (s₁ ^ -s₀ ^ e) v (s₁ ^ s₀ ^ -e)