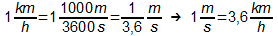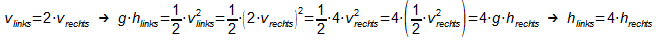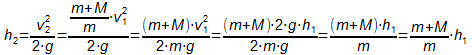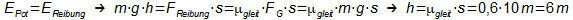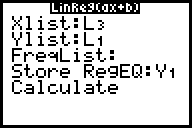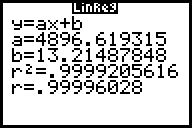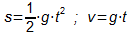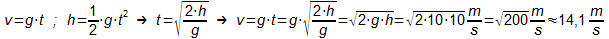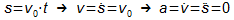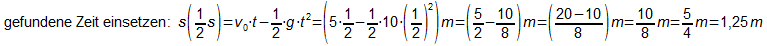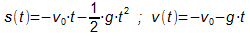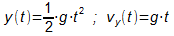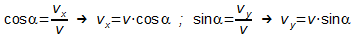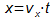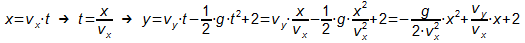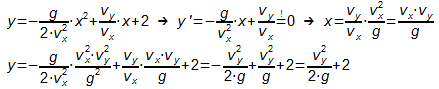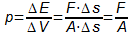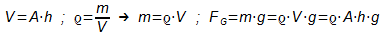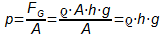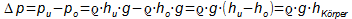Unterrichtseinsichten - Schuljahr 2012/2013 - Physik 10c
Dynamik
2012-09-10
- Die Physik hilft uns, uns in unserer Welt besser zurecht zu finden.
Ein(e) Physiker(in) stellt Fragen an die Natur und versucht aus den
Antworten, die die Natur gibt, Gesetzmäßigkeiten zu finden.
Die Theorien, die die Physiker(innen) auf diese Weise aufstellen,
müssen dann wieder durch neue Versuche geprüft werden.
- Die (mögliche) Erkenntnisgewinnung in der Physik kann z. B.
folgendermaßen ablaufen:
- Man stellt Fragen an die Natur (siehe folgender Versuch)
- Modellbildung (alle Massen fallen gleich schnell)
- Testen des Modells
- auf Stimmigkeit (statt Metallmasse eine Papiermasse gleichen
Volumens: gleicher Fall)
- Versuch der Falsifikation
(→Philosoph Karl
Popper) (eine Metallplatte und eine gleichgeformte
Papierfläche fallen wegen des Luftwiderstands verschieden
schnell)
- Verbesserung des Modells (Vakuumpumpe, Fallröhre s.u.)
- "alle Massen fallen gleich schnell in einem luftleeren Raum und wenn
keine äußeren Kräfte wirken"
- weiter mit 3.
- Zur Einführung in die Dynamik haben wir versucht die Frage
zu klären, ob leichtere oder schwerer Körper schneller fallen:
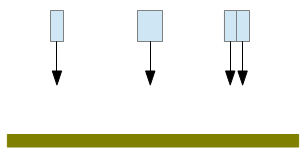
Zunächst soll eine Masse m1 und eine Masse m2
mit m2=2·m1 zur gleichen Zeit die gleiche
Strecke durchfallen (links und Mitte).
Die Abstimmung in der Klasse ergab, dass die größere Masse
schneller unten ankommt als die leichtere Masse.
Diesen Versuchsausgang hat uns unser "gesunder Menschenverstand"
eingegeben und wir befinden uns mit dieser Vorhersage in guter
Gesellschaft.
Unser Versuch zeigte aber, dass beide Massen zur gleichen Zeit unten
ankamen.
- Giovanni
Battista Benedetti (1530 - 1590) hat schon in einem Gedankenexperiment
gezeigt, dass unsere Vermutung (die auch Aristoteles schon
geäußert hat) nicht richtig sein kann:
Halbiert man den größeren Körper, so müsste sich
die Fallzeit verlängern, weil ja jeder Bestandteil des
Körpers leichter ist als der Ausgangskörper.
Mit zusammengeklebten und einzelnen Massestücken haben wir aber
gezeigt, dass das nicht der Fall ist.
- Ein weiterer Versuch zeigte uns, dass unterschiedliche Fallzeiten z.B.
durch den Luftwiderstand bedingt sind:
In einer Glasröhre befinden sich eine Aluminiumkugel, ein
Stück Papier und eine Flaumfeder.
Normalerweise fällt das Aluminiumstück schneller als das
Papier und das Papier schneller als die Feder.

Wird das Rohr aber evakuiert (=die Luft wird aus dem Rohr (wenigstens
teilweise) entfernt), so fallen die 3 Körper fast gleich schnell,
weil
kein Luftwiderstand mehr wirkt.
- Die Beobachtung und anschließende theoretische
Überlegung führen uns also zu folgender Erkenntnis über
unsere Natur:
Alle Körper fallen gleich schnell, ob sie nun schwer oder leicht
sind und welche Form sie auch haben, wenn keine Beeinträchtigungen
(Luftreibung oder andere Kräfte) von außen stattfinden.
- Allgemein gilt:
Physikalische Gesetzmäßigkeiten gelten immer nur in
bestimmten Bereichen.
Werden die Bereichsgrenzen überschritten, müssen die Modelle
und Gesetzmäßigkeiten möglicherweise abgeändert
werden.
2012-09-17
- Ein Bezugssystem ist das System, aus dem heraus ein Versuch beobachtet
wird.
Die günstige Wahl des Bezugssystems erleichtert die Auswertung des
Versuchs.
Im Physikunterricht benutzen wir meistens das Laborsystem (=der
Versuchstisch ist in Ruhe).
- Wiederholung (bzw. für einige neu): Lageenergie oder potentielle
Energie
Wird ein Körper angehoben, so ist die benötigte Arbeit
proportional zur Höhe und proportional zur Masse des Körpers:
W~h und W~m.
Da die aufgewendete Arbeit als Energie E im Körper gespeichert ist
und da sich die Gewichtskraft FG
aus der Masse durch Multiplikation mit dem Ortsfaktor g ergibt, gilt:
E~h und E~m und damit insgesamt E~m·h bzw. (wegen E=F·s)
E=FG·h=m·g·h mit dem
Proportionalitätsfaktor g (Orstfaktor).
- Versuch zur Abhängigkeit der maximalen Geschwindigkeit eines
Pendels von der Auslenkhöhe:

Eine zylinderförmige Masse mit dem Durchmesser 5 cm schwingt
bifilar aufgehängt hin und her.
Die Höhe h der maximalen Auslenkung wird vorgegeben.
Die (maximale) Geschwindigkeit am untersten Punkt der Bahn (233 mm) wird
mit
einer Lichtschranke gemessen (Messung der Verdunkelungs-Zeit,
Berücksichtigung des Körper-Querschnittes).
Messwerte:

- Hausaufgabe: Wie hängt mathematisch die Geschwindigkeit der
Masse im untersten Punkt der Bahn von der maximalen Höhe der Masse
ab?
2012-09-24
- Auswertung des Versuchs aus der letzten Stunde.
Da Ihr in der Klausur den Taschenrechner benutzen müsst, solltet
Ihr Euch unbedingt die Darstelllung dieser Auswertung bei den
Materialien für die Klassen 10e
und 10f
ansehen. Dort seht Ihr Schritt für Schritt, wie man mit dem
Taschenrechner zur Lösung kommt.
Hier die LibreOffice-Calc-Datei,
die wir erstellt haben:

- Am oberen Punkt, dem Ort der größten Auslenkung, besitzt
die Masse nur potentielle Energie.
Ganz unten (an der Lichtschranke), der Stelle größter
Geschwindigkeit, besitzt die Masse nur kinetische Energie.
Aus Energieerhaltungsgründen müssen also diese beiden Energien
gleich sein.
Die potentielle Energie berechnet sich aus EPot=m·g·h.
Die kinetische Energie ist proportional zum Quadrat der Geschwindigkeit
(wie oben gezeigt): EKin~v2.
Sicher wird die kinetische Energie auch proportional zur Masse sein: EKin~m,
also insgesamt EKin~m·v2.
Stimmen eventuell m·g·h und m·v2
überein?
Wir haben mit unseren Messwerten berechnet, dass m·v2
doppelt so groß ist wie m·g·h (1,94-fach).
Damit EPot=EKin, muss also gelten EKin=1/2·m·v2.
- Damit gelten für 2 wichtige Energien folgende Formeln:

2012-10-01
- In der ersten Stunde haben wir besprochen, wie man mit dem
Taschenrechner (statt des Netbooks) die Auswertung des Versuchs
durchführt.
Eine Anleitung dazu findet Ihr auf den Seiten der Klassen 10e
und 10f.
- Aufgaben zum Energieerhaltungssatz
- Wird EPot mit EKin gleichgesetzt, so hebt
sich die Masse durch Division weg. Die untersuchten Vorgänge sind
dann also unabhängig von der Masse.
- Bei Umrechungen zwischen den Einheiten der Geschwindigkeit gilt:
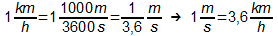
Also: Beim Übergang von den "großen" Einheiten zu den
"kleinen" Einheiten muss man durch 3,6 dividieren, den Wert also
kleiner machen,
beim Übergang von den "kleinen" Einheiten zu den "großen"
Einheiten muss man mit 3,6 multiplizieren, den Wert also
größer machen.
- Versuch zur kinetischen Energie:

Zwischen dem Ende des Maßstabs, der untergelegten Rolle und den
beiden Gummistopfen besteht jeweils ein Abstand von 15 cm.
Wird nun das Ende (rechts) des Maßstabes kräftig nach unten
gedrückt, fliegen die beiden Gummistopfen in die Luft. Welche
Flughöhen werden dabei erreicht?
Vorgeschlagen wurde u. a., die beiden Stopfen würden die gleiche
Höhe erreichne oder der linke Stopfen würde die 2-fache oder
1,5-fache Höhe erreichen. Tatsächlich flog der linke Stopfen
etwa 4-mal so hoch wie der rechte Stopfen. Warum?
Der linke Stopfen besitzt beim Abheben die doppelte Geschwindigkeit wie
der rechte Stopfen, da er sich doppelt so weit vom Auflagepunkt
befindet wie der rechte Stopfen. Also gilt vlinks=2·vrechts.
Was folgt daraus über die Höhen hlinks und hrechts?

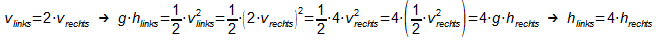
2012-10-08
- Frage: Es sind mehrere Bahnen gegeben, bei denen aus der gleichen
Höhe eine Kugel bis auf eine gleiche tiefere Ebene herunter rollt.
Wie hängt die unten erreichte Geschwindigkeit von der Form der
Bahn ab?

Da oben nur potentielle Energie vorhanden ist und unten nur kinetische
Energie (wenn man von Reibung und anderen störenden Einflüssen
absieht), dann ist die erreichte Geschwindigkeit unabhängig von der
Form der Bahn.
- Aufgabe:
Ein Sportler der Masse m springt von einer
Erhöhung der Höhe h1 mit der zusätzlichen Masse M
beladen auf ein Trampolin. Im tiefsten Punkt lässt er die
zusätzliche Masse los und wird vom Gummituch nach oben
geschleudert. Welche Höhe h2 erreicht er jetzt?
Lösung:
Auf der Erhöhung besitzt der Sportler die potentielle Energie
EPot,1 und keine kinetische Energie.
Im tiefsten Punkt besitzt der Sportler die kinetische Energie EKin,1 und
keine potentielle Energie.
Beim Losfliegen im tiefsten Punkt besitzt der Sportler die kinetische
Energie EKin,2 und keine potentielle Energie.
Beim Erreichen des höchsten Punkts besitzt der Sportler die
potentielle Energie EPot,2 und keine kinetische Energie.

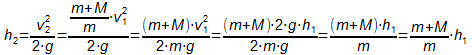
Mit h1=6m, m=60kg und M=20kg ergibt sich h2=80/60*6m=8m.
2012-10-15
- Physikalische Aufarbeitung des Stratosphären-Rekordsprungs
von Felix
Baumgartner.
- Reibung
Im Versuch sollte untersucht werden, wie die Reibung von verschiedenen
Bedingungen abhängt.


- Materialien als Unterlage:
- Styropor
- lackierte Metallplatte
- Pressholzplatte
- Schaumgummi
- Schultisch
- Variationen:
- verschiedene Auflageflächen bei gleicher Masse
- verschiedene Massen bei gleicher Auflagefläche
- verschiedene Geschwindigkeiten
- Benutzung alter Kraftmesser
Die Einheit p bedeutet Pond. 10 p bedeutet, dass eine Masse von 10 g an
dem Kraftmesser hängt.
Gerundet gilt: 100 p = 1 N.
Die Kraftmesser lassen sich nicht mehr alle auf 0 stellen. Der Offset
muss bei den Messungen beachtet werden.
- Auswertung zur nächsten Stunde
2012-11-19
- Ergebnisse zum Thema "Reibung":
- Einen Körper aus der Ruhe in Bewegung zu bringen benötigt
mehr Kraft, als ihn dann weiter zu bewegen.
- Um einen Körper in Bewegung zu verswetzen, muss die
Haftreibungskraft Fhaft überwunden werden.
Fhaft = μhaft · FG ; μhaft
ist der Haftreibungskoeffizient, eine Konstante, die von den sich
reibenden Materialien abhängt.
- Um bei einem Körper die Geschwindigkeit aufrecht zu erhalten,
muss die Gleitreibungskraft Fgleit überwunden werden.
Fgleit = μgleit · FG ; μgleit
ist der Gleitreibungskoeffizient, eine Konstante, die von den sich
reibenden Materialien abhängt.
- Immer gilt μgleit<μhaft.
- Beispielaufgabe zur Reibung:
Ein Auto mit der Geschwindigkeit 100 km/h soll möglichst schnell
bis zur Ruhe abgebremst werden. Dabei blockieren die Räder auf dem
gesamten Bremsweg (Reifen auf nassem Asphalt: μgleit=0,6).
Die Länge des Bremsweges ist zu berechnen.
Lösung:
Die gesamte kinetische Energie wird in innere Energie
überführt:

Der Bremsweg beträgt also etwa 64 m.
- Zur Vorbereitung auf die Klassenarbeit Seiten 125-145 lesen.
2012-11-26
- Wiederholung zur Klassenarbeit
- Anleitung zur Bedienung des Taschenrechners bei der Auswertung einer
Messtabelle findet man bei den Aufzeichungen
zur Klasse 10e (2012-09-28)
- Bei der Klassenarbeit könnte es sinnvoll sein, sich u. a.
folgende Fragen zu stellen und Erkenntnisse in Erinnerung zu rufen:
- Welche Energien sind vorhanden?
- Welche Energien werden benötigt?
- Welche Energien sind mit den auftretenden Kräften
verknüpft?
- Welche Bedingungen bestehen zu Beginn und beim Ende des zu
behandelnden Zeitintervalls?
- Kann man Energien gleichsetzen?
- Kann man Kräfte gleichsetzen?
- Energie ist Kraft (Kraft in Richtung des Weges) mal Weg: E=Fs·s
- Die potentielle Energie ist proportional zur Höhe: EPot=FG·h=m·g·h
- Die kinetische Energie ist proportional zu v2: EKin=1/2·m·v2
- Haftreibung und Gleitreibung sind proportional zur Gewichtskraft
(bzw. zur Normalkraft): Fhaft=μhaft·FG
und Fgleit=μgleit·FG
- Reibungsenergie ist Reibungskraft mal Weg: ER=Fgleit·s
- Zwei Beispiele für Rechnungen
- Schlittenfahrt
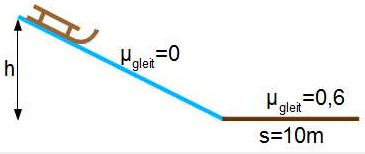
Ein Schlitten gleitet aus einer Höhe h ohne Reibung bis zu einer
Ebene, die schneefrei ist und daher
den Schlitten abbremst (auf einer Strecke s=10m mit dem
Gleitreibungskoeffizienten 0,6). Zu berechnen ist, aus welcher
Höhe der Schlitten startet.
Lösung:
Oben hat der Schlitten nur potentielle Energie. Diese ist genau so
groß wie die Reibungsenergie, die dem Schlitten entzogen wird,
bis er steht.
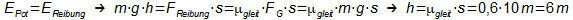
Der Schlitten startet also aus der Höhe 10m.
- Weihnachtsmann
Der Weihnachtsmann schafft es, seinen schweren Geschenksack (m=50kg)
genau 1km über den Boden zu ziehen (μgleit=0,9).
Dann verteilt er die Geschenke und ruht sich so lange aus, dass er
danach mit derselben Energie, die er für das Ziehen des Sacks
gebraucht hat, wieder auf der Himmelsstrickleiter in den Himmel
klettern kann. Oben in seiner Wohnung kommt er wieder vollkommen
erschöpft (also ohne Energie) an.
Wie hoch über dem Erdboden wohnt der Weihnachtsmann (m=100kg)?
Lösung:
Reibungsenergie gleich potentielle Energie:

2012-12-03
2012-12-10
- Bei der Beschreibung von Bewegungen muss man zunächst festlegen,
welches Bezugssystem
man benutzen will.
Das Laborsystem
ist ein ruhendes Bezugssystem. Alle Vorgänge werden in Bezug auf
den Raum, in dem man sich befindet, beschrieben.
Manchmal ist es aber auch sinnvoll, ein bewegtes Bezugssytem zu
verwenden, z.B. das Schwerpunktsystem bei der Untersuchung mehrerer
aufeinander einwirkender Körper, bei dem der Schwerpunkt als ruhend
angenommen wird.
In unterschiedlichen Bezugssystemen können Vorgänge
unterschiedlich aussehen.
- Wir haben den Fall zweier Kugeln untersucht, bei dem eine Kugel ohne
Antrieb senkrecht nach unten fiel und die andere Kugel parallel zum
Erdboden abgeschossen wurde.

Beim Lösen der Schraube wird der dünne zentrale Metallstab
nach rechts gestoßen.
Damit verliert die linke Kugel ihren Halt und fällt senkrecht nach
unten. Die rechte Kugel wird nach rechts geschleudert und fällt
dabei auch nach unten.
Diese Beschreibung ist im Laborsystem abgefasst.
Benutzt man ein gewegtes Bezugssystem, das sich mit der rechten Kugel
nach rechts bewegt, sieht die Lage so aus:
Die rechte Kugel fällt senkrecht nach unten und die linke Kugel
wird scheinbar nach links geschleudert und fällt dabei auch nach
unten.
Da die Vorgänge im bewegten und im ruhenden Bezugssystem
symmetrisch ablaufen, müssen beide Kugeln zur selben Zeit unten
ankommen.
Dieses für manche überraschende Versuchsergebnis haben wir
tatsächlich beobachtet.
- Wie fällt nun eine Kugel nach unten? Fällt sie mit
konstanter Geschwindigkeit oder wird sie schneller?
Wir haben uns in Anlehnung an Galileis Versuche angeschaut, wie eine
Kugel eine schräge Tischplatte herunter rollt.
War die Tischplatte zu steil, konnten wir keinen Unterschied in der
Geschwindigkeit bemerken, aber bei flacher Tischplatte erkannten wir,
dass die Geschwindigkeit zunächst niedrig ist und dann immer mehr
zunahm.
- Für eine genaue Untersuchung benutzten wir ein
Kugelfallgerät:

Aus verschiedenen Höhen wird die Kugel fallen gelassen und trifft
auf einen Auffangtopf.
Die Fallzeit wird mit einem Zählgerät registriert.
Messwerte:

In einem ersten Auswertungsschritt sollte der Zusammenhang zwischen h
und t ermittelt werden.
Der Graph zeigte, dass wohl keine Gerade vorliegt, aber über die
Art der zugehörigen Funktion waren wir uns noch nicht einig.
Durchprobieren der einzelnen Regressionen als Hausaufgabe.




2012-12-17
- Auswertung des Versuchs aus der letzten Stunde:
Mit dem Ansatz "Potenzfunktion" ergibt sich eine gute Annäherung an
die Messwerte:
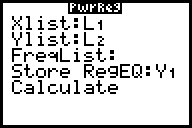


Es gilt also: 
Um den Proportionalitätsfaktor herauszufinden, wird h gegen t2
abgetragen.
Dazu wird in L3 (t) das Quadrat von L2 (t2) gebildet.
Waagrecht wird dann L3 und senkrecht L1 abgetragen:

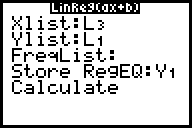
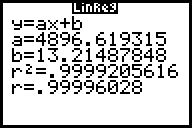

Gerundet gilt also: 
Beachtet man jetzt noch, dass die Höhe in mm gemessen wurde und
rechnet die Werte in m um und ersetzt die Höhe allgemein durch die
Strecke s, so ergibt sich s=5·t2.
Diese Gleichung wird uns dann zu Beginn des neuen Jahres längere
Zeit begleiten.
Über den Zahlenwert 5 werden wir uns dann auch noch unterhalten.
2013-01-07
2013-01-14
- Während der Zensurenbesprechung habt ihr folgenden Versuch
alleine durchgeführt:
- Wird ein Körper der Masse m auf eine Höhe h angehoben, so
besitzt er die potenzielle oder Lageenergie EPot=m·g·h.
Fällt er aus dieser Höhe herunter, so besitzt er beim
Auftreffen auf den Boden keine potenzielle Energie mehr, dafür aber
kinetische oder Bewegungsenergie EKin.
Diese kinetische Energie wird von der Masse m und der Geschwindigkeit
abhängen.
- Der Zusammenhang zwischen der Höhe h bei der potenziellen Energie
und der Geschwindigkeit v bei der kinetischen Energie soll untersucht
werden.
Dazu ein Vorversuch:
- Eine schräge Ebene hat ihren tiefsten Punkt an der Stelle auf
dem Fußboden, der in einer Entfernung zur Wand liegt, die
zweimal so lang wie die schiefe Ebene ist.

Eine Kugel wird auf den obersten Punkt der schiefen Ebene gesetzt und
rollen gelassen.
Sobald die Kugel am unteren Ende der schiefen Ebene angekommen ist,
wird eine zweite Kugel rollen gelassen (siehe obere Zeichnung).
Diese zweite Kugel erreicht zu der Zeit das untere Ende der schiefen
Ebene, zu der die erste Kugel an die Wand stößt (siehe
untere Zeichnung).
Da die 1. Kugel in gleicher Zeit doppelt so viel Weg zurücklegt
wie die 2. Kugel, ist die Geschwindigkeit der 1. Kugel (also die
Geschwindigkeit, die die Kugel am unteren Ende der schiefen Ebene
erreicht), doppelt so groß wie die mittlere Geschwindigkeit
während des Herabrollens auf der schiefen Ebene.
- Anders ausgedrückt:
Wird bei der gleichmäßigen Beschleunigung im
Gravitationsfeld der Erde die Wegstrecke und die Zeit vom Beginn der
Bewegung bis zu einem Messpunkt registriert, so kann man aus dieser
Wegstrecke und der Zeit die mittlere Geschwindigkeit des bewegten
Körpers berechnen. Diese mittlere Geschwindigkeit ist halb so
groß wie die Geschwindigkeit, die der Körper am Messpunkt
erreicht hat, also v=2·vmittel.
- Der Vorversuch fand an einer schrägen Ebene mit
verschiedenen Neigungswinkeln statt, aber in Gedanken (und in
Wirklichkeit) können wir den Neigungswinkel auf 90°
erhöhen, sodass wir mit dem Fallversuch aus der letzten Stunde vor
den Weihnachtsferien die Beziehung v=2·vmittel
überprüfen können.
Wir haben das mit Hilfe eines Tabellenkalkulationsprogramms
durchgeführt:
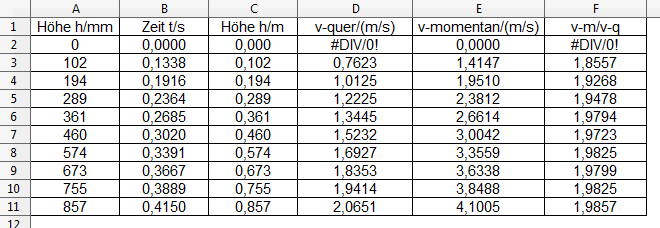
Die gemessenen Werte für die Höhe h (Spalte A) und die Zeit t
(Spalte B) wurden übernommen vom 2012-12-10.
Die Höhe wird umgerechnet in die Einheit m (Spalte C).
Die Durchschnittsgeschwindigkeit v-quer wird in Spalte D berechnet mit
v-quer=h/t.
Über den Energieerhaltungssatz wird v-momentan beim Auftreffen in
Spalte E berechnet:

Um die Beziehung v=2·vmittel bzw.
v-momentan=2·v-quer zu überprüfen, wird dann v-momentan
durch v-quer dividiert.
Die Werte liegen sehr nahe bei 2 und bestätigen damit die Vermutung
v=2·vmittel.
2013-01-21
- Vor den Ferien haben wir schon erkannt, dass der Zusammenhang
zwischen zurückgelegter Strecke und der vergangenen Zeit durch
s=5·t2 gegeben ist.
Zunächst wurde dieses Ergebnis noch einmal mit Hilfe der Tabelle
nachvollzogen.
Dannhaben wir untersucht, wie sich die Momentangeschwindigkeit bei
verschiedenen Höhen zur Zeit verhält.
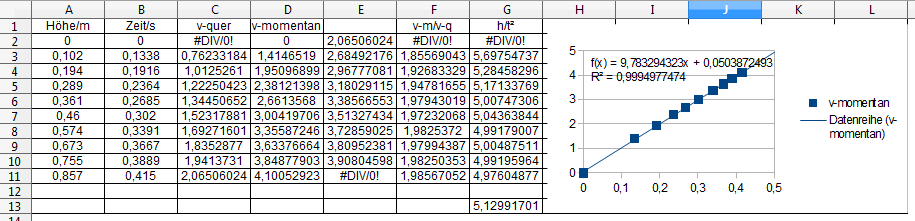
Das Diagramm zeigt uns, dass v proportional zu t ist (v~t).
Die zugehörige Funktionsgleichung heißt (bei Rundung)
v=10·t.
Der Proportionalitätsfaktor 10 (natürlich später noch
mit Einheit) wird sicher vom Versuchsort (Erde, Mond ...) abhängen
und da er den Wert 10 hat, scheint man dafür auch den Ortsfaktor g
schreiben zu dürfen.
In der Gleichung für s kommt 5 vor, die Hälfte von 10 und
deshalb könnte man da die Hälfte des Ortsfaktor-Werts
einsetzen können.
Insgesamt ergibt sich dann für die Gleichungen des freien Falls:
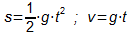
- An zwei kleinen Aufgaben haben wir gesehen, wie man die Gleichungen
des freien Falls einsetzen kann:
- Aufgabe:
Ein Körper fällt aus 39 km Höhe zur Erdoberfläche.
Wie lange würde der Fall dauern, wenn es keine Luftreibung
gäbe?
Lösung:

Die Fallzeit würde also etwa 1,5 Minuten betragen.
In Wirklichkeit war Felix
Baumgartner
bei seinem Sprung aus 39 km Höhe wegen des Luftwiderstandes
wesentlich länger unterwegs (siehe auch Links vom 2012-10-15).
- Aufgabe:
Welche Geschwindigkeit erreicht man am Boden, wenn man aus 10 m
Höhe (ohne Luftwiderstand) fällt?
Lösung:
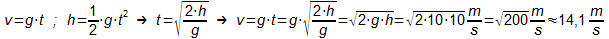
Da hier die Zeit gar keine Rolle spielkt, hätten wir auch die
schon bekannten Gleichungen für die Energie zur Lösung
benutzen können:

2013-01-28
- Durch Ableiten erhält man aus den Weg-Gleichungen von
Bewegungsgleichungen die Geschwindigkeits- und
Beschleunigungsbesziehungen.
- Beispiele
- geradlinig gleichförmige Bewegung:
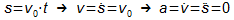
- beschleunigte Bewegung (freier Fall):

- Beispielrechnung zum senkrechten Wurf:
Aufgaben
Ein Ball der Masse m = 100 g wird aus der Höhe 1,5 m mit der
Geschwindigkeit v0 = 5 m/s senkrecht nach oben geworfen
(g=10m/s²).
1. Wie viel Zeit vergeht, bis der Ball seine größte Höhe
erreicht hat?
2. Um wie viel Meter steigt der Ball insgesamt an?
3. Wie lange dauert es, bis der Ball auf der Erde auftrifft?
Lösungen
Es überlagern sich 2 verschiedene Bewegungen: eine
geradlinig-gleichförmige Bewegung nach oben und eine beschleunigte
Bewegung (freier Fall) nach unten. Daraus ergeben sich folgende
Bewegungsgleichungen:

zu 1.:

zu 2.:
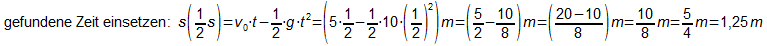
zu 3.:
da die t Achse in der Höhe 1,5 liegt, wird die Erde bei s(t)=-1,5
erreicht:


Der Fall dauert also 1,24 s.
2013-02-08
- Weitere Fälle zu Wurfbewegungen
- senkrechter Wurf nach unten
Es werden dieselben Formeln verwendet wie beim senkrechten Wurf nach
oben.
Nur das Vorzeichen der Terme, die die Bewegung mit konstanter
Geschwindigkeit angeben, wird geändert:
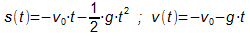
- waagrechter Wurf
Die Bewegungen in x- und in y-Richtung sind unterschiedlich:
In x-Richtung liegt eine Bewegung mit konstanter Geschwindigkeit vor:

In y-Richtung liegt eine beschleunigte Bewegung vor: 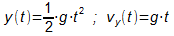
Fasst man die Ortsgleichungen zusammen und entfernt die Zeit t, so
erhält man die Gleichung der Bahnkurve (Parabel):

2013-02-15
- Schiefer Wurf
Eine Wurfkugel soll aus der Höhe 2m möglichst weit geworfen
werden.
Dazu darf sie weder waagrecht (Wurfwinkel 0°) noch senkrecht
(Wurfwinkel 90°), sondern mit einem Winkel zwischen 0° und
90° geworfen werden.
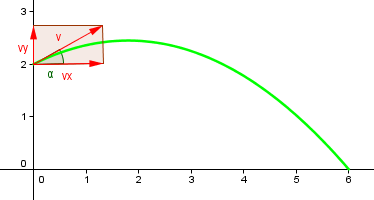
- Für die Bewegungsgleichungen benötigt man die x-Komponent vx
und die y-Komponente vy der Geschwindigkeit v:
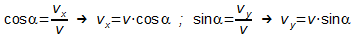
In x-Richtung bewegt sich die Kugel mit der Geschwindigkeit vx
nach rechts:
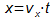
In y-Richtung bewegt sich die Kugel mit der Geschwindigkeit vy
nach oben und im freien Fall nach unten mit Start auf der Höhe 2m:

- Die Gleichung für die Flugbahn erhält man, wenn man den
Parameter t aus den beiden Gleichungen entfernt:
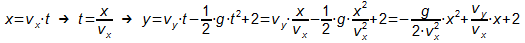
Es ergibt sich als Flugbahn eine Parabel (quadratische Funktion).
- Wie weit vom Werfer entfernt ist die Kugel am höchsten und welche
Höhe erreicht sie dabei?
Lösung: Die Ableitung der Funktionsgleichung wird gleich 0 gesetzt.
Der x-Wert gibt die Entfernung an und der zugehörige y-Wert die
Höhe.
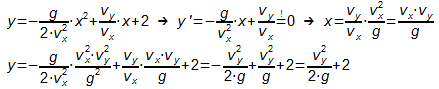
- Hausaufgabe: Weite des Wurfs bestimmen, wenn gegeben sind: v0=7m/s
und Winkel 45°.
2013-02-22
- Lösung der Hausaufgabe:
Weite des Wurfs bestimmen, wenn gegeben sind: v0=7m/s und
Winkel 45°.
Die Weite ergibt sich durch die Bedingung y=0 (die Kugel erreicht den
Erdboden).
Die entstehende quadratische Gleichung muss gelöst werden. Dann
werden die Werte eingesetzt.
Dazu müssen vorher noch die vx- und vy-Werte
mit Hilfe des Winkels berechnet werden.


Die größte Weite ergibt sich für den Fall mit dem
Pluszeichen:

Die Kugel erreicht also eine Wurfweite von 6,4 m.
- Unter welchem Winkel sollte man die Kugel abstoßen, damit
sie mit vorgegebener Anfangsgeschwindigkeit möglichst weit fliegt?
Dazu rechnet man den Auftreffpunkt x aus und interpretiert ihn als
Funktion des Winkels.
Leitet man nun nach dem Winkel ab und setzt die Ableitung gleich 0,
ergibt sich der Winkel für die größte Weite.
Wegen der Schwierigkeit der Rechnung haben wir nur mit GeoGebra die
Funktion x(α) dargestellt und die Ableitung an jeder Stelle durch einen
Punkt mit der Option "Spur ein" gezeichnet:
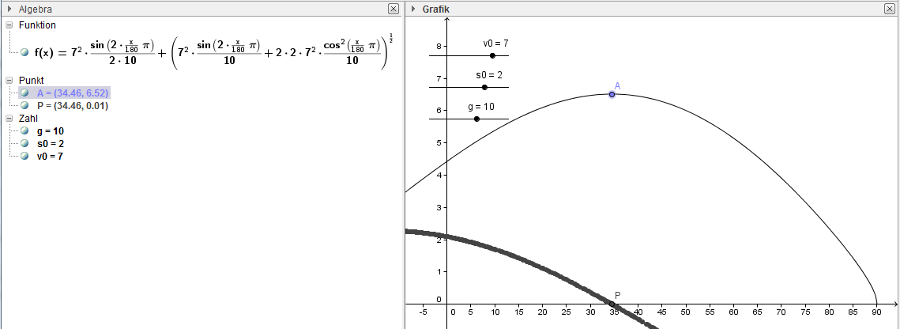
Man sieht, dass ein Winkel von etwas weniger als 35° am geeignetsten
ist.
2013-03-01
- Die Aufgabe zu Super-Mathio haben wir mit der Simulation
in Geogebra und rechnerisch gelöst (zum Laden der
GeoGebra-Datei Klick auf das Bild):
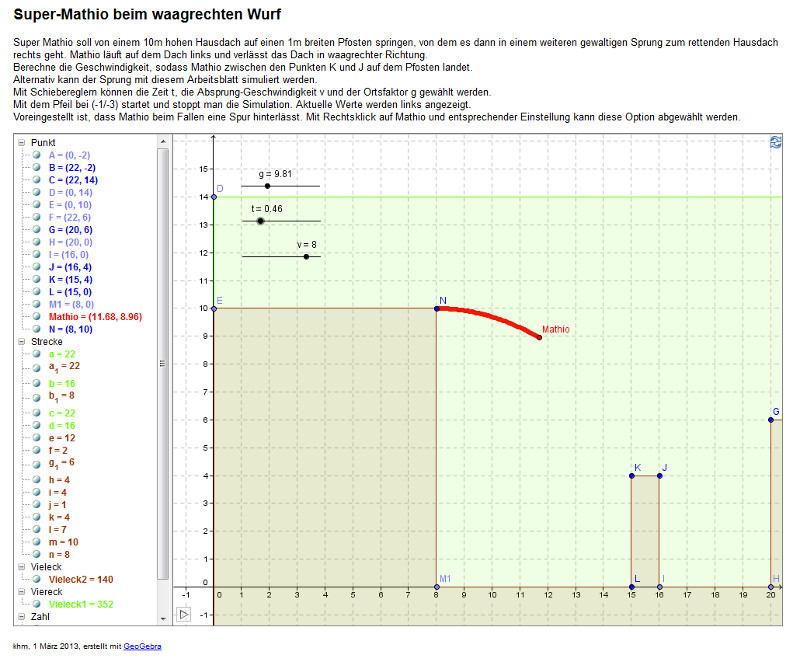
Super-Matio soll aus 10 m Höhe am Punkt N(8/10) waagrecht
abspringen und zwischen K(15/4) und J(16/4) landen. Die
Absprung-Geschwindigkeit v ist gesucht.
Lösungsidee:
1. Mit Hilfe der Koordinaten von N die Bewegungsgleichungen aufstellen.
2. t aus den Gleichungen entfernen, so dass nur noch y in
Abhängigkeit von x gegeben ist.
3. Mit Hilfe der Koordinaten von K und J Gleichungen aufstellen, aus
denen sich der jeweilige v-Wert ergibt.

Super-Mathio muss also eine Geschwindigkeit zwischen 6,3 m/s und 7,2 m/s
besitzen, wenn er auf dem Pfosten ankommen will.
- Kennenlernen der Luftkissenfahrbahn, mit der in der nächsten
Stunde ein Zusammenhang zwischen der Kraft F und der Beschleunigung a
bei einer beschleunigten Bewegung gefunden werden soll.

2013-03-08
- Zusammenhang zwischen der beschleunigenden Gewichtskraft und der
Beschleunigung des Fahrbahnwagens:
Die Gesamtmasse des Wagens und der Massestücke wurde mit der Waage
zu 93 g bestimmt.

Dann wurde der Wagen mit 2 bis 7 Massestücken (1g pro
Massestück) beschleunigt.
Die Auswertung erfolgte mit Hilfe des Cassy-Interfaces:
Registriert wurde die Wegstrecke in Abhängigkeit von der Zeit.
Eine geräte-interne Umrechnung (1. Ableitung für die
Geschwindigkeit und 2. ABleitung für die Beschleunigung) erlaubte
dann, die Beschleunigung festzustellen:
Als Beispiel hier das Messergebnis für die Beschleunigung mit 2
angehängten Massestücken:
t-s-Diagramm
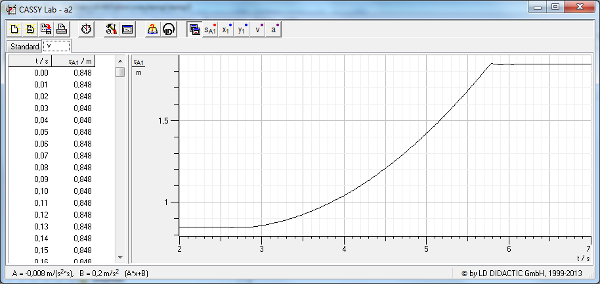
t-v-Diagramm
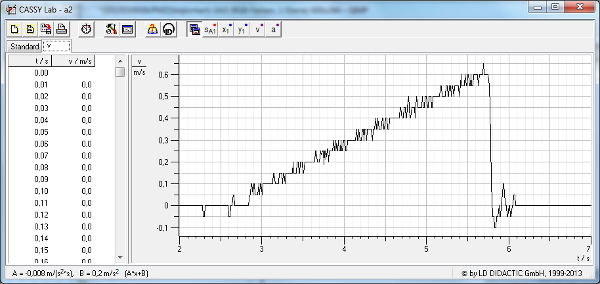
t-a-Diagramm (Die Ausgleichsgerade hat einen durchschnittlichen a-Wert
von 0,2 m/s²)

- Messergebnisse als Tabelle:

- Auswertung mit LibreOffice

x ist die Anzahl der beschleunigenden Massestücke.
Die Gewichtskraft dieser Massestücke berechnet sich aus Masse mal
Ortsfaktor (Spalte C).
Die Auswertung (lineare Regression) liefert etwa F=92,4g·a
- Der Proportionalitätsfaktor stimmt mit der Gesamtmasse des
Wagens plus Massestücke überein. Deshalb gilt F=m·a.
Mit einer zusätzlich aufgelegten Masse von 100 g wurde das bei 7
beschleunigenden Massestücken bestätigt:
Masse m=93g, Beschleunigung a=0,72m/s² : m·a=0,07N
Masse m=193g, Beschleunigung a=0,35m/s² : m·a=0,07N
2013-03-15
- Übungen zur Newtonsche Bewegungsgleichung F=m·a.
2013-04-05
- Wiederholung zur Arbeit
- Wurfbewegungen
Wichtig ist:
- Koordinatensystem festlegen
- Alle Bewegungsarten in x- und y-Richtung berücksichtigen.
- Für jede Bewegungsart wird der entsprechende Formelterm
addiert.
- Koordinaten gegebener Punkte in die Formeln einsetzen, um gesuchte
Größen berechnen zu können.
- Newtonsche Bewegungsgleichung F=m·a
2013-04-12
- Wiederholung zur Arbeit
- Im Zusammenhang mit der Newtonschen Bewegungsgleichung
F=m·a muss mit den Formeln für die beschleunigte Bewegung
gerechnet werden, da eine wirkende Kraft den Bewegungszustand einer
Masse verändert.
2013-04-19
2013-04-26
- Einführung in die Kreisbewegung:
Die Auswirkungen einer schnellen Drehung auf einen Ball haben wird am
Drehtisch beobachtet:

Der blaue Ball sollte so durch die Klemme gestützt werden, dass
er beim Drehen nicht herunterfiel. Weder auf der linken noch auf der
rechten Seite der Klemme wurde der Ball gehalten. Wurde er dagegen wie
auf dem Bild von den 2 Spitzen der Klemme berührt, fiel er bei der
Drehbewegung nicht von der Platte. Da die Zentrifugalkraft radial nach
außen wirkt, wurde der Ball von der auf das Zentrum zielenden
Zentripetalkraft der Klemme gehalten.
2013-05-03
- Versuch zur Zentripetalkraft
Mit dem Zentralkraftgerät wird die Zentripetalkraft in
Abhängigkeit von der Masse, dem Radius und der
Winkelgeschwindigkeit untersucht.

- Messwerte und Auswertung:
- Kraft in Abhängigkeit von der Masse

- Kraft in Abhängigkeit vom Radius
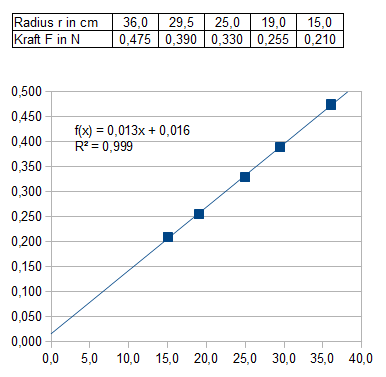
- Kraft in Abhängigkeit von der Winkelgeschwindigkeit
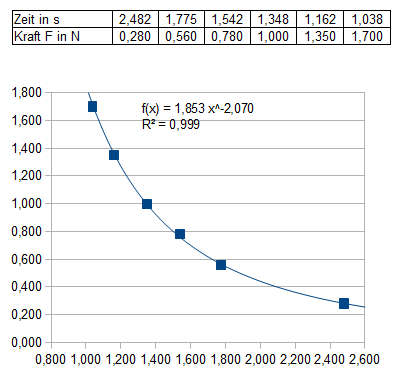
- Weitere Auswertung in der nächsten Stunde.
2013-05-17
- Besprechung und Rückgabe der Klassenarbeit 2 [ Aufgaben
| Lösungen
]
- Winkelgeschwindigkeit ω
Da bei einer Drehbewegung die bewegten Orte abhängig vom Radius
unterschiedliche Bahngeschwindigkeiten besitzen, sucht man nach einer
Größe, die für alle bewegten Orte gleich ist.
Man nimmt dafür den Winkel.
Zur Beschreibung der Drehgeschwindigkeit gibt man dann an, um wieviel
der Winkel pro Zeiteinheit zugenommen hat.
Die Winkel werden dabei im Bogenmaß angegeben.
Im Bogenmaß entspricht dem Winkel 360° die Größe 2π
(Umfang des Einheitskreises mit dem Radius 1).
Die Größe Winkel pro Zeit nennt man Winkelgeschwindigkeit ω:

- Auswertung des Versuchs aus der letzten Stunde:
Die 3 Versuche haben ergeben:
- Die Kraft ist proportional zur Masse: F~m
- Die Kraft ist proportional zum Radius: F~r
- Die Kraft ist proportional zu 1 geteilt durch das Quadrat der
Umlaufdauer und damit proportional zum Quadrat der
Winkelgeschwindigkeit: F~ω²
Insgesamt gilt also: F~m·ω²·r. Bei Messungen findet
man, dass der Proportionalitätsfaktor 1 (einheitenlos) sein muss.
Ergebnis: F=m·ω²·r.
2013-05-31
- Wir haben 2 verschiedene Anwendungen zur Kreisbewegung behandelt und
gesehen, dass derselbe Ansatz zur Lösung führt:
- Berechne die Umdrehungsdauer der Erde für den Fall, dass man am
Äquator auf Grund der Fliehkraft schwerelos wäre.
- Eine
kreisförmige Raumstation mit dem Radius r soll sich so schnell
drehen, dass man am Rande der Station das Gefühl hat, auf dem
Erdboden zu stehen (g=10 m/s²).
- Ansatz zur Lösung: Die Zentripetalkraft ist gleich der
Gewichtskraft:

- Druck - Einführung in den Begriff mit Beispielen:
- Drauckausbreitung

Dieses fast schon antike Gerät besitzt einen Rundkolben, der
ringsum Auslassöffnungen besitzt.
Mit einem Stempel kann man Wasser in diesen Rundkolben pumpen, so dass
sich dort ein erhöhter Druck ausbildet, der das Wasser durch die
Öffnungen nach außen spritzt.
Das Wasser entfernt sich dabei radial vom Glaskolben.
Deutung: Der Druck breitet sich im Kolben in alle Richtungen gleich
aus. Aus demselben Grund ist auch eine Seifenblase rund, falls keine
anderen Kräfte auf sie wirken.
- Kompression von Materie

Befindet sich im verschlossenen Kolbenprober Wasser, so lässt sich
dieses nicht zusammendrücken. Wasser ist inkompressibel.
Ist dagegen Luft im Kolben, so lässt sich das Luftvolumen leicht
verringern. Wird der Kolben aber freigegeben, schwingt er zurück,
sodass das ursprüngliche Luftvolumen wieder hergestellt wird.
Luft ist also kompressibel.
- Die um das Volumen ΔV komprimierte Luft erhält durch die
Kompression die Energie ΔE, die dazu benutzt werden kann, um das
ursprüngliche Volumen wieder herzustellen.
Wegen ΔE=F·Δs (Δs ist der Weg des Kolbens) und ΔV=A·Δs (A
ist die Querschnittsfläche des Kolbens) sind ΔE und ΔV
proportional, weil bei n-fachem Δs auch ΔE und ΔV ver-n-facht werden.
Den Proportionalitätsfaktor nennt man "Druck" p.
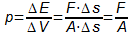
Druck ist also Kraft pro Fläche.
Einheit des Drucks ist N/m²=Pa (Pascal). Meist benutzt man die
Einheit hPa (Hektopascal, 1 hPa = 100 Pa).
2013-06-07
- Druck in Flüssigkeiten

Über der Fläche A befindet sich eine Wassersäule der
Höhe h.
Der Druck auf A wird durch die Gewichtskraft FG des Wassers
bewirkt.
Über das Volumen V und die Dichte ϱ kann man FG
berechnen:
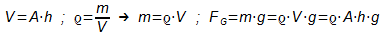
Der Druck p ergibt sich dann zu
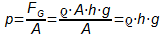
- In der Pausenhalle haben wir den Luftdruck gemessen.
Ein mit Wasser gefüllter durchsichtiger Gartenschlauch wurde mit
dem geschlossenen Ende nach oben gezogen, wobei das andere Ende unten
in einer Wanne unter Wasser gehalten wurde.
Der Wasserstand pegelte sich bei etwa 10 m Höhe ein. Darüber
war im Schlauch kein Wasser (nahezu Vakuum) zu sehen.
Zur Rechnung mit ϱ=1 g/cm³ , g=10 N/kg und h =10m: Der Wasserdruck
und damit der Luftdruck beträgt etwa 1000 hPa.
- Auftrieb

Ein im Wasser befindlicher Körper erfährt von allen Seiten
Druck.
Oben ist der Druck aber geringer als unten, weil die Wassersäule
über dem Körper oben nicht so hoch ist.
Wassesäule oben: ho, Wassersäule unten: hu.
Die seitlichen Drücke heben sich gegenseitig auf.
Berechnung des Druckunterschieds:
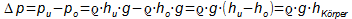
Berechnung der insgesamt nach oben wirkenden Kraft:

Da sich die Dichte auf Wasser bezieht, ist die wirkende Kraft so
groß wie die Gewichtskraft von Wasser, das den Raum der
Körpers einnimmt.
Man kann auch sagen: Die Auftriebskraft ist so groß wie die
Gewichtskraft des vom Körper verdrängten Wassers.