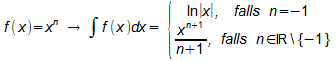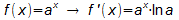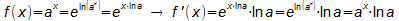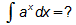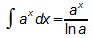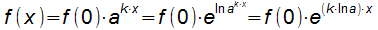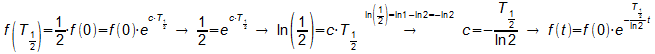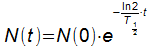Unterrichtseinsichten - Schuljahr 2011/2012 - Mathematik 11ma3g
e-Funktion und natürlicher Logarithmus
2011-12-15
- Hier das Tafelbild mit den Überlegungen zum Problem y=y'. Genauere Ausführungen finden Sie hier.

2011-12-20
- Im Mittelpunkt der Stunde stand der Zusammenhang zwischen kontinuierlicher Verzinsung und Eulerscher Zahl e: Es gilt
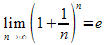 (Beweis)
(Beweis)
Genauere Ausführungen im Skript.
- Rückgabe der Klausur 2 [ Aufgaben | Lösungen ]
2012-01-05
- Wir haben den Begriff Umkehrfunktion kennengelernt und als
Beispiel die Logarithmusfunktion (Basis e) als Umkehrfunktion zur
e-Funktion behandelt.
- Machmal ist die Ableitung einer Funktion schwieriger als die der Umkehrfunktion, wie z. B. bei f(x)=ln x.
Mit Hilfe der Ableitung der Umkehrfunktion haben wir herausgefunden: f(x) = ln x → f ' (x) = 1/x.
Wir haben damit auch den fehlenden Fall bei der Integration von Potenzfunktionen herausgefunden:
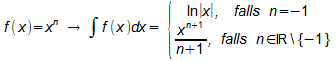
- Nachzulesen ist alles im Script.
2012-01-10
- Ableitung der allgemeinen Exponentialfunktion:
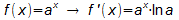
Herleitung:
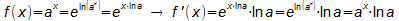
- Integration der allgemeinen Exponentialfunktion:
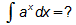
Die Ableitung der gesuchten Stammfunktion muss gleich ax sein.
Mit Hilfe der oben hergeleiteten Ableitung der allgemeinen Exponentialfunktion kann man leicht raten, dass
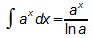
- Nachzulesen sind diese Herleitungen im Script.
2012-01-12
- Wachstums- und Zerfallsprozesse können oft durch Exponenzialfunktionen beschrieben werden: f(x)=f(0)·ak·x.
Für die Basis a kann immer die Eulersche Zahl e benutzt werden. Der Einfluss der Basis a wird dann durch die Konstante (k·ln a) wahrgenommen:
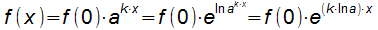
- Die Halbwertzeit T1/2 ist die Zeit, in der sich die
Hälfte eines Bestandes zersetzt hat, wenn die Zersetzung mit einer
bestimmten Wahrscheinlichkeit zufällig erfolgt.
Mit Hilfe des Wertes von T1/2 kann der Exponent der e-Funktion aussagekräftiger geschrieben werden:
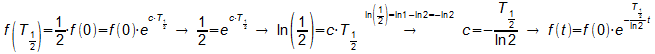
2012-01-17
- Anwendungen des gelernten Stoffs bei Aufgaben zur
exponeziellen Abnahme bei radioaktivem Zerfall und bei Gabe von
Beteubungsmitteln im Rahmen von Operationen.
Angewendet werden musste die Formel
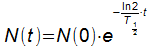
und die Auflösung nach t:
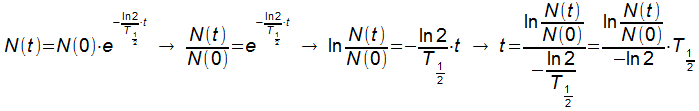
2012-01-24
weiter mit Häufigkeitsverteilungen