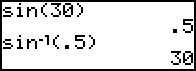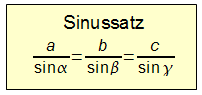Unterrichtseinsichten
- Schuljahr 2010/2011 - Mathematik 9c
Trigonometrie
2010-09-20
- Besprechung und Rückgabe der Klassenarbeit 1 [ Aufgaben | Lösungen ]
- Aufgabe zur Einführung in die Trigonometrie
Südlich von Freiburg befindet sich die Schauinslandbahn (erste Umlaufseilbahn der Welt), die Personen von der Höhe 550m auf den Schauinsland (Höhe 1300m) bringt.

Aufgaben:
Nach 2100m Fahrt bleibt die Gondel der Seilbahn wegen eines Defekts stehen.
a) Bei wieviel Meter über Normal-Null blieb die Gondel stehen?
b) Welchen Höhenunterschied müssen die Passagiere nun zu Fuß bis zur Bergstation zurücklegen?
c) Wieviel Prozent beträgt die Steigung der Drahtseilbahn?
d) Wie groß ist der Winkel α, unter dem die Drahtseilbahn ansteigt?
Lösung:
zu a):
H=1300m - 550m = 750m
Nach dem 2. Strahlensatz gilt 
Die Gondel ist also auf der Höhe 550m + 437,5m = 987,5m, d.h. also bei 987,5m NN stehen geblieben.
zu b):
1300m - 987,5m = 312,5m
Die Passagiere müssen also noch einen Höhenunterschied von 312,5m zu Fuß zurücklegen.
zu c):
Der prozentuale Anstieg einer Strecke ergibt sich aus der Steigung der Strecke, hier also aus H/a.
Dazu muss zunächst a mit Hilfe des Pythagoras berechnet werden: 
Berechnung der prozentualen Steigung: 
zu d):
Wir
haben bislang noch keine Möglichkeit kennengelernt, im allgemeinen
Fall aus den Längen in Dreiecken oder anderen Figuren auf die
Winkel zurückzuschließen.
Andererseits wissen wir aus den
Strahlensätzen, dass das Verhältnis entsprechender Seiten
gleich ist, wenn sich der Winkel zwischen den Strahlen nicht
ändert.
Der Winkel α ist also ganz eng gekoppelt mit dem Verhältnis von Seiten.
Die Verhältnisse  sind gleich und werden mit sin α (sprich: Sinus alpha) bezeichnet.
sind gleich und werden mit sin α (sprich: Sinus alpha) bezeichnet. - Zu jedem Winkel α erhält man mit sin α das Verhältnis zweier Seiten eines rechtwinkligen Dreiecks.
Die
Bestimmung der Sinuswerte ist leider nicht einfach. Früher hat man
in jahrelanger Arbeit Listen mit Sinuswerten für alle
möglichen Winkel berechnet.
Heute
geht das mit dem Taschenrechner einfacher: SIN-Taste drücken und
dann den Winkel eingeben. Dabei darauf achten, dass unter MODE in der
3. Zeile DEGREE eingestellt ist.
Aus einem Verhältnis bekommt man den zugehörigen Winkel so: 2ND + SIN drücken, dann das Verhältnis eingeben.
Beispiele:
sin 30° = 0,5 ; Taschenrechner: SIN(30)
30°
= arcsin 0,5 ; Taschenrechner: 2ND SIN(0.5) ;
arcsin wird Arkussinus gesprochen und auf dem Taschenrechner
durch sin-1 dargestellt.
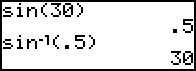
- In
einem rechtwinkligen Dreieck werden die Seiten mit Kathete (Seite liegt
am 90°-Winkel) und Hypotenuse (HY) (Seite liegt dem 90°-Winkel
gegenüber) bezeichnet.
Die Kathete, die an einem betrachteten
Winkel α liegt, heißt Ankathete (AK), die Seite, die dem
Winkel gegenüberliegt, heißt Gegenkathete (GK).
Außer dem Sinus (sin) werden auch Seitenverhältnisse durch den Kosinus (cos) und den Tangens (tan) definiert.

2010-09-24
- Übungen zu Winkel- und Dreiecksseitenberechnung mit Hilfe von sin, cos und tan.
- Hausaufgabe: Seite 68 Aufgaben 10d,e und 11d,e
2010-09-27
- Die
meisten Sinuswerte lassen sich nicht durch einen kurzen Term angeben,
sondern müssen näherungsweise bestimmt werden oder aus
Tabellen oder mit dem Taschenrechner ermittelt werden.
Ausnahmen bilden u.a. die Sinuswerte für die Winkel 30°, 45° und 60° 
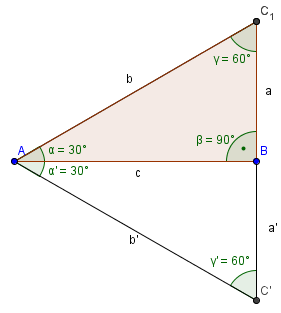
Im
roten rechtwinkligen Dreieck ist der Winkel α=30° gegeben.
Damit hat der dritte Winkel die Winkelgröße 60°.
Spiegelt man das Dreieck an der Seite c, so ergibt sich ein gleichseitiges Dreieck (alle Winkel 60°).
Es gilt sin α = a/b. Da a+a'=b, gilt b=2a.
Also folgt sin α = a/b = a/(2a) = 1/2.

Im
roten rechtwinkligen Dreieck ist der Winkel α=45° gegeben.
Damit hat der dritte Winkel auch die Winkelgröße 45°.
Das Dreieck ist also gleichschenklig und es gilt a=c.
b kann man nun mit dem Satz des Pythagoras berechnen: 
Damit gilt: 
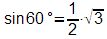

Im
roten rechtwinkligen Dreieck ist der Winkel α=60° gegeben.
Damit hat der dritte Winkel die Winkelgröße 30°.
Spiegelt man das Dreieck an der Seite a, so ergibt sich ein gleichseitiges Dreieck (alle Winkel 60°).
a ist die Höhe im gleichseitigen Dreieck, c ist halb so lang wie b, also b=2c.
Damit lässt sich a berechnen: 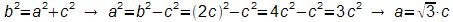
Damit gilt: 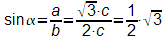
- Zusammenhang zwischen sin und cos

Es
gilt sinα=a/c und cosβ=a/c, also sinα=cosβ
mit β=90°-α, also sinα=cos(90°-α)
und sin(90°-α)=cosα. - Zusammenhang zwischen sin, cos und tan
Es gilt 
- Tabelle mit sin-, cos- und tan-Werten für spezielle Winkel

oder zum besseren Merken nach Umformen einiger sin- und cos-Werte:

2010-10-25
- Wiederholung zu den trigonometrischen Funktionen sin, cos und tan.
Siehe dazu auch das GeoGebra-Arbeitsblatt:
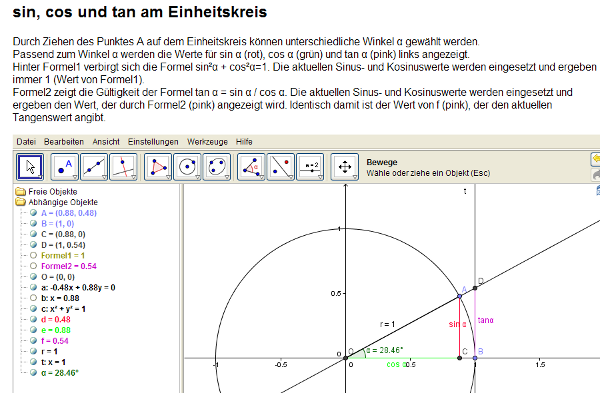
- Bei Aufgaben, die mit sin, cos und tan gelöst werden können, folgende Punkte beachten
- Wo finde ich rechtwinklige Dreiecke?
- Für sin, cos und tan benötige ich 2 Seiten und einen Winkel.
- Welche
Funktion haben die beiden Seiten im Dreieck? (Katheten oder Hypotenuse?
Ankathete oder Gegenkathete?) Welche Winkelfunktion passt dazu (sin,
cos, tan).
- sin-, cos- oder tan-Beziehung aufschreiben und nach der gesuchten Größe auflösen.
- Hausaufgabe: Seite 74, Aufgabe 4 und Seite 75, Aufgabe 8 jeweils ganz
2010-10-27
- Die Hausaufgabe mit der Prozentangabe für die Steigung lässt sich so sehr einfach lösen:

6%
Steigung bedeutet, dass eine Rampe oder Straße nach einer
waagrechten Ausdehnung von 100 (beliebige Längeneinheit) eine
Höhe von 6 aufweist.
Man kann also einfach rechnen: 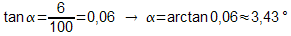
- Hausaufgabe: Seite 67/77 Aufgaben 14, 19, 20
2010-11-03
- Bei
vielen Aufgaben zur Trigonometrie kommt es darauf an, durch
Zeichnungen, Einfügen von Hilfslinien und Lösung von
Teilaufgaben den Lösungsweg vorzuplanen und das Vorgehen klar und
deutlich erkennbar zu halten - für sich selbst und für den,
der die Lösung liest.
Hier ein Beispiel: - Berechne den Winkel α, der sich zwischen einer Raumdiagonalen und einer Kante (Länge a) eines Würfels befindet.

Idee: Wenn man die Längen von a und d kennt, kann man mit cos α=a/d den Winkel α berechnen.
a ist gegeben, d erhält man aus dem rechts abgebildeten Schnittgebilde mit dem Satz des Pythagoras aus d2=e2+a2.
e erhält man aus der in der Mitte abgebildeten Teilfigur mit dem Satz des Pythagoras aus e2=a2+a2.
Die benötigten Teilfiguren werden nicht perspektivisch verzerrt mit Angabe der Eckpunkte gezeichnet.
Folgende Teilüberlegungen ergeben nun die Lösung: - Es fällt auf:
 Strecke - 1-dimensional
Strecke - 1-dimensional Fläche - 2-dimensional
Fläche - 2-dimensional Volumen - 3-dimensional
Volumen - 3-dimensional
- Diese
Gesetzmäßigkeit gilt auch, wenn die Seitenlängen nicht
gleich sind. Dann müssen der Reihe nach bei der Erhöhung der
Dimension die Quadrate der einzelnen Seitenlängen unter der Wurzel
addiert werden. Der Satz vom Pythagoras gilt also auch in anderen
Dimensionen als der 2.Dimension (in der Ebene).
2010-11-08
- Berechnungen an beliebigen Dreiecken
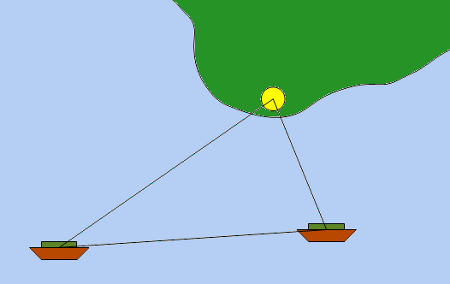
Ein Schiff fährt von links nach rechts an einer Landzunge vorbei.
Links sieht man den Leuchtturm unter dem Winkel α=36°, rechts unter dem Winkel β=68°.
Der Weg von der linken bis zur rechten Position beträgt 9km.
Wie weit ist das Schiff rechts vom Leuchtturm entfernt?
Lösung:
Planfigur: 
c=9 ; α=36° ; β=68°
Zunächst wird im Dreieck ABD die Länge von hc berechnet.
γ
ist der Ergänzungs winkel von α und β zu
180°: γ=180°-α-β=180°-36°-68°=76°
Im Dreieck BCD wird dann mit Hilfe von γ und hc die Seitenlänge von a bestimmt.
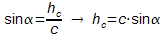
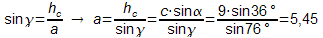
Das Schiff ist am Ort B also rund 5,5km vom Leuchtturm bei C entfernt. - Die gefundene Formel lässt sich umschreiben nach
 .
.
Da
keine speziellen Werte enthalten sind und das Dreieck ohne
besondere Eigenschaften ist, ist das Ergebnis auch auf b und
sin β erweiterbar.
Diese Gesetzmäßigkeit nennt man Sinussatz:
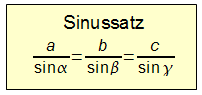
- Anmerkung: Beim stumpfwinkligen Dreieck liegt die verwendete Höhe außerhalb des Dreiecks.
Man
erhält dann statt sin α möglicherweise sin
(180°-α), statt sin β möglicherweise sin
(180°-β) und statt sin γ möglicherweise
sin (180°-γ).
Da aber sin α = sin (180°-α) für jeden Winkel α, ändert sich am Sinussatz nichts.
2010-11-10
- An Hand der Sportplatzaufgabe haben wir den Kosinussatz hergeleitet:

Vom
Ort S (Start) wirft ein Sportler einen Diskus. Dieser landet im Ziel
bei Z. Gefragt ist die Entfernung zwischen S und Z (Strecke a für
Abstand).
Am Punkt B (Beobachter) befindet sich ein Lasergerät,
das die Entfernungen zwischen S und B (Strecke b) und zwischen Z und B
(Strecke c) und auch den Winkel α zwischen den Strecken b und c
messen kann.
Aus den Größen b, c und α muss nun die Länge der Strecke a ermittelt werden:
Einzeichnen von Hilfslinien: 
Rechnung:
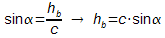


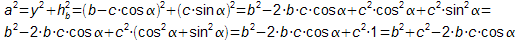

- Da wir nicht mit speziellen Werten sondern allgemein mit Buchstaben gerechnet haben, können wir das Zwischenergebnis a2=b2+c2-2·a·b·cos(α) verallgemeinern:
Wenn
in einem Dreieck 2 Seiten und der eingeschlossene Winkel bekannt sind,
kann man das Quadrat der 3. Seite berechnen nach folgender Formel:

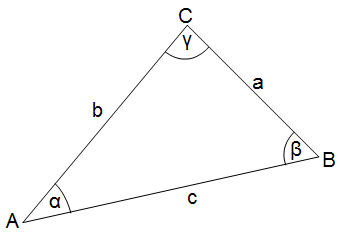
- Anmerkung:
Der Satz des Pythagoras ist ein Spezialfall des Kosinussatzes: Ist
einer der Winkel α, β oder γ gleich 90°, so
fällt der letzte Summand im Kosinussatz weg und der Satz des
Pythagoras bleibt stehen.
2010-11-15
- Zwei
Wanderer haben sich in der Wüste verlaufen und sind sich uneins,
wie sie weiter gehen sollen, um zur nächsten Oase zu gelangen.
Schließlich
trennen sie sich und gehen jeder auf vollkommen geraden Wegen weiter,
die zueinander einen Winkel von 40° bilden.
Als der eine erste
Wanderer nach genau 970m Strecke (mit einem Schrittzähler
gemessen) auf die Oase trifft, ruft er über Satellitentelefon den
Mitwanderer an, der in dieser Zeit genau 430m zurückgelegt hat.
Aufgaben:
Wie weit ist der 2. Wanderer noch von der Oase entfernt? Um wieviel
Grad muss er nun von seinem Weg abweichen, um zur Oase zu gelangen?
Planfigur (nicht maßstabsgerecht!): 
- Lösung:
- Der Abstand von B zur Oase wird mit dem Kosinussatz berechnet:

- Den Winkel β kann man entweder mit dem Sinussatz oder dem Kosinussatz berechnen:
- Sinussatz:

- Kosinussatz:

- Die
Verwirrung ist groß: Es gibt zwei unterschiedliche Ergebnisse,
die sich aber (das sieht man leicht) zu 180° ergänzen.
Die Lösung des Problems ergibt sich durch die Veranschaulichung des Sinus am Einheitskreis (GeoGebra-Arbeitsblatt):

Im Bereich zwischen 0° und 180° gibt es 2 Winkel mit gleichem Sinus-Wert.
Der Taschenrechner gibt aber nur den Winkel aus, der zwischen 0° und 90° liegt.
Beim
Berechnen eines Dreiecks- Winkels mit dem Sinussatz muss man also immer
kontrollieren, ob der gesuchte Winkel nicht vielleicht
größer als 90° sein muss.
Besser ist es, mit dem Kosinussatz den Dreiecks-Winkel zu berechnen. Dabei erhält man mit Sicherheit den richtigen Wert.
In unserer Aufgabe ist der korrekte Winkel also β=116,7°. - Winkel δ ergibt sich als Ergänzungswinkel zu β zu δ=180°-116,7°=63,3°.
- Der
2. Wanderer muss also um 63,3° von seiner ursprünglichen
Richtung abweichen und dann noch 698m gehen, bis er die Oase erreicht
hat.
- Flächenberechnung eines Dreiecks mit Hilfe des Sinus:

Die Dreiecksfläche berechnet sich mit Hilfe der Formel A=1/2·g·h (g=Grundseite, h=Höhe).
Es seien im abgebildeten Dreieck die Seiten b und c und auch der Winkel α bekannt.
Nimmt man Seite b als Grundseite, so kann man die Höhe hb aus α und c bestimmen:

In der Formel kommen 2 Seiten und der eingeschlossene Winkel vor.
Aus Symmetriegründen gilt deshalb auch:

2010-11-17
2010-11-22
- Der Mittelpunktswinkel ist immer doppelt so groß wie der Umfangswinkel.
Zur Veranschaulichung dient das GeoGebra-Arbeitsblatt:

Es gilt γ=γ1+γ2.
Wegen des Umkreises sind die Radien alle gleich: r=r1=r2=r3.
Die Dreiecke AMC und BCM sind gleichschenklig. Deshalb gilt γ1=γ1' und γ2=γ2'.
Aus
der Winkelsumme 180° in einem Dreieck folgt
β=180°-2·γ1
und δ=180°-2·γ2.
Daraus
folgt
α=360°-β-δ=360°-(180°-2·γ1)-(180°-2·γ2)=2·γ1+2·γ2=2·γ,
also das Doppelte von γ. - Zieht man C so, dass r1 und r2 den Durchmesser des Kreises bilden, so entsteht bei B ein Winkel von 90° und es gilt:
 .
.
Da a die Seite ist, die dem Winkel γ gegenüberliegt, gilt der erweiterte Sinussatz:  .
.
2010-11-24
- Übungen mit Anwendungsaufgaben (prozentuales Gefälle, Vorwärtseinschneiden)
2010-11-29
- Flächeninhalt eines Dreiecks mit Inkreisradius ρ

Das
Dreieck wird in drei Teildreiecke aufgeteilt, deren Eckpunkte neben 2
Eckpunkten des Dreiecks noch der Mittelpunkt des Inkreises sind.
Der Inkreisradius ρ ist die Höhe auf den Seiten der Teildreiecke, die auch Seiten des großen Dreiecks sind.
Damit
wird die Fläche jedes Teildreiecks aus der Hälfte des
Produkts einer Dreieckseite mit dem Inkreisradius gebildet:
AΔABM=0,5·c·ρ ; AΔBCM=0,5·a·ρ ; AΔCAM=0,5·b·ρ
Die gesamte Fläche aller Teil-Dreiecke, also des großen Dreiecks wird damit zu AΔ =0,5·a·ρ+ 0,5·b·ρ+0,5·c·ρ=0,5·(a+b+c)·ρ - Flächeninhalt einer Raute

Der Flächeninhalt einer Raute berechnet sich aus Grundseite mal Höhe.
Die Höhe kann mit dem Sinus bestimmt werden. Daraus ergibt sich:

- Lichtbrechung beim Übergang von Luft ins Wasser

Tritt Licht aus der Luft ins Wasser über, so wird die Richtung des Lichts geändert.
Gegenüber dem Einfallslot wird der Winkel kleiner. Man sagt:
Beim Übergang vom optisch dünneren ins optisch dichtere Medium wird das Licht zum Einfallslot hin gebrochen.
Der Brechungsindex n gibt an, wie stark das Licht gebrochen (=abgelenkt) wird.
Es gilt: 
- Aufgabe: Der Brechungsindex sei n=1,3 und der Einfallswinkel wird zu α=50° gemessen. Welchen Wert hat Winkel β?

- Wie groß kann Winkel β höchstens werden?
α kann maximal 90° werden. Eingesetzt in die Formel ergibt sich dann der größte Wert für β:

2010-12-01
- Wiederholung zur Arbeit
- Bergaufgabe:
Auf einem Berg steht ein Turm der Höhe t, dessen Unterkante aus
dem Tal unter dem Höhenwinkel α und dessen Oberkante unter
dem Winkel β gesehen wird.
Die Höhe des Berges ist zu berechnen.

Es gilt 
2010-12-06
weiter mit Vierfeldertafeln und Baumdiagramme