Unterrichtseinsichten
- Schuljahr 2009/2010 - Mathematik 9a
Rückschlüsse aus Baumdiagrammen
2009-12-10
- Soll
ein Sachverhalt untersucht werden, bei dem nach 2 Kriterien
unterschieden wird, die jeweils zutreffen können oder nicht
zutreffen können, so bietet sich als Hilfsmittel zur
Veranschaulichung eine 4-Felder-Tafel an:
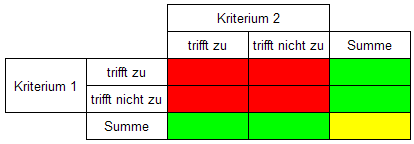
In
den roten Feldern steht, in welchem Maß die Kriterien 1 und 2
zutreffen, die grünen Felder enthalten die Summen der roten
Spalten- bzw. Zeilen-Felder, das gelbe Feld enthält die Summe der
roten Felder. - Beispiel: In einer Umfrage werden die
Schülerinnen und Schüler der 9. Jahrgangsstufe befragt, ob
sie einen eigenen Computer besitzen, der höchstens 2 Jahre alt ist.
Die Darstellung der Ergebnisse der Umfrage erfolgt in einer 4-Feldertafel:
Kriterium 1: Junge oder Mädchen ; Kriterium 2: besitzt Computer oder besitzt keinen Computer.
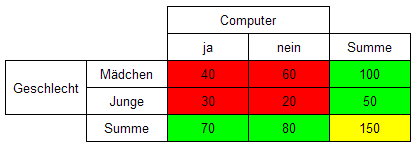
- Aus dieser Darstellung lassen sich nun leicht einige Aussagen ableiten:
- Fast
die Hälfte besitzt einen eigenen neueren Computer (die Summe 70
für "Computer -ja" ist nur geringfügig kleiner als die Summe
80 für "Computer - nein").
- 40% der Mädchen haben
einen eigenen Computer (insgesamt sind es 100 Mädchen, 40
Mädchen haben einen eigenen Computer, das sind 40%).
- Etwa
57% alle Computerbesitzer sind Mädchen (insgesamt gibt es 70
Computerbesitzer, darunter 40 Mädchen. Das ergibt 40/70=4/7 oder
etwa 0,57).
- Mehr Mädchen als Jungen besitzen einen
Computer (40 Mädchen aber nur 30 Jungen geben an, einen eigenen
Computer zu besitzen, also gibt es mehr Mädchen mit Computer.
Betrachtet man aber nicht die absoluten Zahlen sondern den jeweils
prozentualen Anteil, dann ergibt sich ein anderes Bild: 40% (40 von
100) der Mädchen und 60% (30 von 50) der Jungen besitzen einen
eigenen Computer, also gibt es prozentual mehr Jungen als Mädchen,
die einen eigenen Computer besitzen).
- Wir haben
herausgefunden, dass mindestens 4 Werte der 9 farbigen Felder bekannt
sein müssen, damit die 4-Felder-Tafel ganz ausgefüllt werden
kann. Dabei dürfen aber nicht mehr als 2 Werte in einer Zeile oder
einer Spalte stehen (denn die 3. Zahl in jeder Reihe und in jeder
Spalte lässt sich aus den beiden anderen Zahlen errechnen).
- Hausaufgabe: Krimi-Frage auf Seite 101
2009-12-16
- Hier in leichter Abwandlung die richtige Lösung der Krimiaufgabe:
Bei einem Einbruch findet man ein gebrauchtes Taschentuch, das dem Täter gehören muss.
10 Personen stehen unter Verdacht, den Einbruch begangen zu haben, aber nur eine Person kann ihn durchgeführt haben.
Von den 10 Personen fängt man nur eine einzige und führt einen DNA-Test durch.
Wenn die Person der Täter war, wird zu 100% die Übereinstimmung angezeigt.
Wenn die Person unschuldig ist, kann es trotzdem in 1/3 aller Fälle beim Test zu einer Übereinstimmung kommen.
Sollte man den Vedächtigen auf Grund des positiv ausgefallenen Tests verurteilen? - Lösung: Erstellung einer 4-Felder-Tafel.
Vorgehen:
1. Insgesamt sind es 10 Personen.
2. 1 Person ist schuldig.
3. 9 Personen sind unschuldig.
4.
Ist der Täter schuldig, fällt der Test garantiert positiv aus
(bei einer Poson also 1 positiver Test und 0 negative Testergebnisse).
5.
Ist der Täter unschuldig, so gibt es 1/3 positive und 2/3 negative
Ergebnisse (bei 9 Personen also 3 positive und 6 negative Ergebnisse).
6. Die Anzahl aller positiv und aller negativ Getesteten ergibt sich aus einfacher Addition. - In den 4-Felder-Tafeln ist links die Reihenfolge der Bearbeitung angegeben und rechts sind die Werte eingetragen.

Wenn man alle Personen testen würde, würde bei 4 Personen der Test positiv ausfallen.
1
Person von diesen 4 Personen wäre aber nur schuldig, d.h. die
Wahrscheinlichkeit, schuldig zu sein, wenn man positiv getestet wird,
ist lediglich 1/4.
Der Gefangene ist also nur zu 25% der Einbrecher.
2010-01-08
- Ausführliche Besprechung der Aufgaben der letzten Mathematikarbeit.
Bitte
arbeitet die Aufgaben auch selbstständig zu Hause durch, damit die
Wiederholungsarbeit in einer Woche besser ausfällt! - Zu den nächsten Stunden bitte die Formelsammlung mitbringen.
2009-01-13
- In der Formelsammlung findet Ihr die wichtigsten Formeln für die Trigonometrie auf den Seiten 26 und 27
- Die
alte Arbeit haben wir jetzt vollständig besprochen. Ihr habt gut
aufgepasst und wenn Ihr jetzt noch die einzelnen Aufgaben selbst ohne
Hilfe durchrechnet, kann eigentlich am Freitag nur alles gut werden!
- Wir schreiben am Freitag in der 1. und 2. Stunde in Eurem Klassenraum J07.
2010-01-15
2010-01-20
- Um
nach langer Pause wieder in das eigentliche Thema einzusteigen, haben
wir folgende Situation in einer 4-Felder-Tafel und in Baumdiagrammen
dargestellt:
In einer Urne liegen 10 Kugeln, davon sind 6 Kugeln gelb und 4 rot.
Auf 2 gelben Kugeln steht eine 0, auf den anderen gelben Kugeln eine 1.
Bei den roten Kugeln trägt 1 Kugel eine 0 und die anderen eine 1.
Wie groß ist die Wahrscheinlichkeit für das Ziehen einer Kugel mit bestimmter Farbe und Aufschrift?



Die
mittleren Brüche (in cyan) ergeben sich daraus, dass man die
Brüche rechts durch die entsprechenden Brüche links dividiert.
Die schwarz geschriebenen Brüche findet man auch in der 4-Felder-Tafel wieder.
Die
cyan-farbigen Brüche ergeben sich aus der Division eines Bruchs
aus den mittleren 4 Feldern mit einem Bruch in der "gesamt"-Spalte bzw.
"gesamt"-Reihe. - Hausaufgabe: Auf gleiche Art die "Flensburger-Punkte-Aufgabe" bearbeiten.
2010-01-27
- An einer Uni ist die Durchfallquote bei Klausuren sehr hoch.
Die Klausuren dürfen aber mehrmals nachgeschrieben werden.
Folgende 2 Texte befassen sich mit dem Abschneiden bei den Klausuren. - 75% der Teilnehmer einer Klausur schreiben die Klausur zum 1. Mal. Von diesen Teilnehmern bestehen 73% die Klausur.
Von den übrigen Teilnehmern, die die Klausur wiederholen, fallen 43% wieder durch. - Bei einer Klausur fallen 31% der Teilnehmer durch. 34% davon sind Wiederholer.
20% derjenigen, die die Prüfung bestehen, wiederholen die Klausur.
- Auf
den ersten Blick sieht man nicht die Gemeinsamkeit in beiden Texten.
Legt man aber eine 4-Felder-Tafel an, so sieht man, dass dieselbe
Situation beschrieben wird.

Die durch die Texte direkt gegebenen Felder sind gelb unterlegt.
Auch
wenn die Werte im Innern der Tafel nicht exakt übereinstimmen,
kann man erkennen, dass die Texte aus denselben Daten gewonnen wurden. - Hausaufgabe: Aufgabe zum Diabetes-Test.
2010-02-10
- Die Lösung zum Diabetes-Test steht im Buch auf den Seiten 110 und 111
- Wichtige Vereinbarungen bei Wahrscheinlichkeiten
- Bei einem Baumdiagramm bezieht sich die erste Verzweigung immer auf die Gesamtheit.
Wird
nach einem Kriterium K1 unterschieden, das die Werte "ja" und "nein"
annehmen kann, so schreibt man für die Wahrscheinlichkeiten
p(K1ja) und p(K1nein) - Die zweite Verzweigung hat als Bezugsgröße die Menge derjenigen, die die erste Bedingung erfüllen.
Wird bei der zweiten Verzweigung nach einem Kriterium K2 unterschieden (Werte "ja" und "nein"), so schreibt man
in Fortsetzung der Verzweigung K1ja für die Wahrscheinlichkeiten pK1ja(K2ja) und pK1ja(K2nein) und
in Fortsetzung der Verzweigung K1nein für die Wahrscheinlichkeiten pK1nein(K2ja) und pK1nein(K2nein). - Die
Gesamtwahrscheinlichkeit für einen Pfad beträgt das Produkt
der Wahrascheinlichkeiten am Pfad und enthält die
Wahrscheinlichkeit dafür, dass alle Kriterien entlang des Pfades
erfüllt sind.
Für das Ergebnis schreibt man z.B. p(K1ja ∩ K2nein).
- Gesamtübersicht für einen zu einer 4-Felder-Tafel gehörenden Baum:

- Die Wahrscheinlichkeiten an der ersten Verzweigung stehen in der 4-Felder-Tafel am rechten oder unteren Rand.
Die Wahrscheinlichkeiten ganz rechts im Baumdiagramm stehen in der 4-Felder-Tafel in den mittleren 4 Feldern.
Die
Wahrscheinlichkeiten an der zweiten Verzweigung können berechnet
werden durch "mittleres Feld dividiert durch Randfeld".
Beispiel: 
- Hausaufgabe: Seite 113 Aufgaben 4 und 6
2010-02-11
- In den letzten Stunden haben wir uns mit bedingten Wahrscheinlichkeiten beschäftigt.
Bei solchen Rechnungen können sehr leicht Fehler unterlaufen.
Wir haben dazu zwei Beispiele (Wettspiele) untersucht: - 3 Karten,
von denen eine Karte auf beiden Seiten rot, die zweite Karte auf beiden
Seiten grün und die dritte Karte auf der einen Seite rot und auf
der anderen Seite grün eingefärbt ist, werden verdeckt
gemischt. Eine Karte wird dann verdeckt gezogen. Wenn man richtig
rät, welche Farbe auf der Rückseite ist, hat man gewonnen.
Mit welcher Wahrscheinlichkeit gewinnt man?

Folgende Lösungsvorschläge haben wir diskutiert: - Wenn rot oben liegt, muss unten rot oder grün liegen, also gilt p(rot)=1/2 und p(grün)=1/2.
- Wenn
rot oben liegt, dann gibt es noch 5 Kartenseiten, die man nicht sieht,
davon 2 rote und 3 grüne, also gilt p(rot)=2/5 und
p(grün)=3/5.
- Wenn rot oben liegt, dann kann es nicht die Karte sein, die auf beiden Seiten grün ist.
Es gibt nur noch 3 Seiten mit 2-mal rot und 1-mal grün. Also gilt p(rot)=2/3 und p(grün)=1/3. - Die Wahrscheinlichkeit, die 2-farbige Karte gezogen zu haben, beträgt 1/3.
Wenn rot oben liegt, folgt damit p(grün)=1/3 und p(rot)=2/3. - In
einer Simulation habt Ihr in 9 Gruppen das Spiel simuliert. Gefragt war
dabei, ob die gleiche Farbe oder die andere Farbe bei der gezogenen
Karte verdeckt lag.
Hier die Ergebnisse: 
Zur Auswertung haben wir alle Ergebnisse zusammengefasst und herausgefunden:
p(gleiche Farbe)=93/(93+61)=93/154≈0,604=60,4%≈3/5
p(andere Farbe)=61/(93+61)=61/154≈0,396=39,6%≈2/5
- Mit
einer 6-Felder-Tafel kann man die richtige Wahrscheinlichkeit leicht
erkennen (ebenso geht es natürlich auch mit Baumdiagrammen):

Zur Erläuterung: - Die
Summen unten geben an, mit welcher Wahrscheinlichkeit eine bestimmte
Karte gezogen wird, die Summen rechts, mit welcher Wahrscheinlichkeit
eine bestimmte Farbe gezogen wird.
- Da Karte 1 ganz rot ist,
wird für grün/Karte1 eine 0 eingesetzt und folglich bleibt
für rot/Karte1 nur 1/3 übrig.
- Da Karte 2 ganz
grün ist, wird für rot/Karte1 eine 0 eingesetzt und folglich
bleibt für grün/Karte1 nur 1/3 übrig.
- Auf Karte 3 sind beide Farben gleich verteilt, also gilt für jede Farbe die Wahrscheinlichkeit 1/2·1/3=1/6.
- Hat man nun eine rote Farbe gezogen (p=1/2), so gilt prot(Karte1)=p(verdeckt ist rot)=(1/3)/(1/2)=2/3 und prot(Karte3)=p(verdeckt ist grün)=(1/6)/(1/2)=1/3.
- Zum
Ziegenrätsel haben wir bisher nur eine Simulation
durchgeführt. Die Auswertung und die Theorie folgen dann in der
nächsten Stunde.
- Hausaufgabe: Seite 113 Aufgabe 7
2010-02-17
- Lösung zum Ziegenrätsel:
- Das
Rätsel: Bei einem Gewinnspiel stehen 3 Türen zur Auswahl.
Hinter einer Tür steht ein Auto, hinter den anderen beiden
Türen eine Ziege (=Niete).
Man darf zunächst eine Tür raten. Dann öffnet der Spielleiter eine Tür, hinter der eine Ziege steht.
Nun
wird man aufgefordert zu entscheiden, ob man bei der ersten getroffenen
Wahl bleibt oder ob man zu der noch geschlossenen Tür wechselt.
Wenn man die Tür mit dem Auto geraten hat, gewinnt man das Auto.
Lohnt sich ein Wechsel zur vorher nicht gewählten Tür? - Lösung: Beim ersten Raten hat man bei 3 Türen die Chance 1/3, dass man die Tür mit dem Auto rät.
Für beide anderen Türen zusammen gilt die Wahrscheinlichkeit 2/3, dass dort das Auto steht.
Wenn
der Spielleiter die eine der beiden Türen öffnet, gilt
für die andere Tür die Wahrscheinlichkeit 2/3. Also lohnt es
sich, auf diese Tür zu wechseln.
Man gewinnt dann mit der Wahrscheinlichkeit 2/3 das Auto. - Andere
Lösung: Man schreibt sich alle Möglichkeiten für den Ort
des Autos und die geratene Tür auf und zählt dann nach, wie
oft man Erfolg hat:

6-mal
"ja" stehen 3-mal "nein" gegenüber, d.h. bei 9 Möglichkeiten
hat man beim Wechsel die Chance 6/9=2/3, das Auto zu gewinnen.
- Bei
der Besprechung der Hausaufgabe haben wir gesehen, dass sich bei einem
wiederholten Test das Baumdiagramm um eine Pfadverzweigung erweitert.
An der 2. und 3. Verzweigung stehen dann für die beiden Tests dieselben Wahrscheinlichkeiten.
Dazu auch die Hausaufgabe: Seite 114 Aufgabe 8
2010-02-18
- Die Hausaufgabe haben wir intensiv besprochen.
Wir
haben gesehen, dass es sehr wichtig ist, genau zu definieren
(=festzulegen), was bei einem Test "positiv" und "negativ" bedeutet.
Hier unser korrigiertes (und nun hoffentlich fehlerfreies) Tafelbild:


Das Baumdiagramm unten gilt für den Fall, dass 2-mal unabhängig voneinander geprüft wurde.
2010-02-19
- Wiederholung zur Arbeit
- Wie findet man zu einem Baumdiagramm das umgekehrte Baumdiagramm?
Erklärung an Hand des ersten Tafelbildes der letzten Stunde: - während
im linken Baumdiagramm zuerst nach f und nf und dann nach pos und neg
unterschieden wurde, wird im rechten Baumdiagramm zuerst nach pos und
neg unterschieden.
Um
rechts die Wahrscheinlichkeit für pos und neg zu finden, werden
links am rechten Rand die Wahrscheinlichkeiten für nf und pos und
f und pos addiert: 0,005+0,882=0,887. Das ist die Wahrscheinlichkeit
für den Fall pos im rechten Baumdiagramm.
Ebenso wird für
neg links aus den beiden Angaben 0,095 und 0,018 die Wahrscheinlichkeit
0,113 für neg im rechten Diagramm berechnet. - Die
Wahrscheinlichkeiten am jeweils rechten Rand eines Baumdiagramms
stimmen links und rechts überein. Die mittleren Werte stehen nur
an einer anderen Stelle.
- Die Wahrscheinlichkeiten an der
zweiten Verzweigung ergeben sich aus der Division der Werte ganz rechts
durch die Werte an der ersten Verzweigung.
- Die Werte an
den ersten Verzweigungen der Baumdiagramme finden sich in der
4-Felder-Tafel in den Summenspalten unten und rechts wieder.
Die Werte rechts außen an den Baumdiagrammen finden sich in den 4 mittleren Felder der 4-Felder-Tafel wieder.
2010-02-24
weiter mit Potenzen - Exponentialfunktionen













